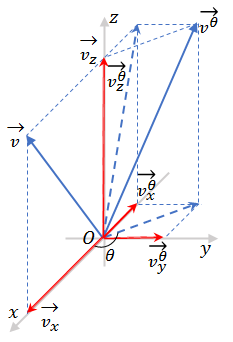
第一部分: R o d r i g u e s Rodrigues Rodrigues(罗德里格斯)公式描述的是:空间内的任意一个向量 v \textbf{v} v,绕指定的旋转轴 k \textbf{k} k旋转 θ \theta θ角度,得到空间向量 v θ \textbf{v}^{\theta} vθ的过程。 R o d r i g u e s Rodrigues Rodrigues公式利用 v \textbf{v} v, k \textbf{k} k和 θ \theta θ来描述 v θ \textbf{v}^{\theta} vθ。
如图所示,空间内的向量
v
\textbf{v}
v,绕着
z
z
z轴旋转
θ
\theta
θ,得到
v
θ
\textbf{v}^{\theta}
vθ。已知
x
x
x轴,
y
y
y轴和
z
z
z轴的方向向量分别是
i
\textbf{i}
i,
j
\textbf{j}
j和
k
\textbf{k}
k。约定
<
a
,
b
>
<\textbf{a},\textbf{b}>
<a,b>表示向量
a
\textbf{a}
a到向量
b
\textbf{b}
b的夹角。
对于空间向量
v
\textbf{v}
v可以分解为三个坐标轴上的投影向量的矢量和:
v
=
v
x
+
v
y
+
v
z
\textbf{v} = \textbf{v}_x + \textbf{v}_y + \textbf{v}_z
v=vx+vy+vz
其中:
v
y
=
0
\textbf{v}_y = \textbf{0}
vy=0
v
z
=
∣
∣
v
∣
∣
⋅
cos
<
k
,
v
>
⋅
k
=
∣
∣
v
∣
∣
⋅
∣
∣
k
∣
∣
⋅
cos
<
k
,
v
>
⋅
k
=
(
k
⋅
v
)
⋅
k
\textbf{v}_z = ||\textbf{v}|| \cdot \cos{<\textbf{k}, \textbf{v}>} \cdot \textbf{k} = ||\textbf{v}|| \cdot ||\textbf{k}|| \cdot \cos<\textbf{k}, \textbf{v}> \cdot \textbf{k} = (\textbf{k} \cdot \textbf{v}) \cdot \textbf{k}
vz=∣∣v∣∣⋅cos<k,v>⋅k=∣∣v∣∣⋅∣∣k∣∣⋅cos<k,v>⋅k=(k⋅v)⋅k
v
x
=
∣
∣
v
∣
∣
⋅
sin
<
k
,
v
>
⋅
i
\textbf{v}_x = ||\textbf{v}|| \cdot \sin<\textbf{k}, \textbf{v}> \cdot \textbf{i}
vx=∣∣v∣∣⋅sin<k,v>⋅i
对于
v
x
\textbf{v}_x
vx来说,可以得到以下变换:
∣
∣
v
∣
∣
⋅
sin
<
k
,
v
>
=
∣
∣
v
∣
∣
⋅
∣
∣
k
∣
∣
⋅
sin
<
k
,
v
>
=
∣
∣
k
×
v
∣
∣
||\textbf{v}|| \cdot \sin<\textbf{k}, \textbf{v}> = ||\textbf{v}|| \cdot ||\textbf{k}|| \cdot \sin<\textbf{k}, \textbf{v}> = ||\textbf{k} \times \textbf{v}||
∣∣v∣∣⋅sin<k,v>=∣∣v∣∣⋅∣∣k∣∣⋅sin<k,v>=∣∣k×v∣∣
i
=
j
×
k
\textbf{i} = \textbf{j} \times \textbf{k}
i=j×k,又有
j
=
k
×
v
∣
∣
k
×
v
∣
∣
\textbf{j} = \frac{\textbf{k} \times \textbf{v}}{||\textbf{k} \times \textbf{v}||}
j=∣∣k×v∣∣k×v,则
i
=
1
∣
∣
k
×
v
∣
∣
⋅
k
×
v
×
k
\textbf{i} = \frac{1}{||\textbf{k} \times \textbf{v}||} \cdot \textbf{k} \times \textbf{v} \times \textbf{k}
i=∣∣k×v∣∣1⋅k×v×k
因此,可以得到:
v
x
=
∣
∣
k
×
v
∣
∣
⋅
1
∣
∣
k
×
v
∣
∣
⋅
k
×
v
×
k
=
k
×
v
×
k
\textbf{v}_x = ||\textbf{k} \times \textbf{v}|| \cdot \frac{1}{||\textbf{k} \times \textbf{v}||} \cdot \textbf{k} \times \textbf{v} \times \textbf{k} = \textbf{k} \times \textbf{v} \times \textbf{k}
vx=∣∣k×v∣∣⋅∣∣k×v∣∣1⋅k×v×k=k×v×k
同理,对于
v
θ
\textbf{v}^{\theta}
vθ也可以分解为
v
θ
=
v
x
θ
+
v
y
θ
+
v
z
θ
\textbf{v}^{\theta} = \textbf{v}_x^{\theta} + \textbf{v}_y^{\theta} + \textbf{v}_z^{\theta}
vθ=vxθ+vyθ+vzθ
其中:
v
z
θ
=
v
z
\textbf{v}_z^{\theta} = \textbf{v}_z
vzθ=vz
v
x
θ
=
∣
∣
v
x
∣
∣
⋅
cos
θ
⋅
i
=
v
x
⋅
cos
θ
=
k
×
v
×
k
⋅
cos
θ
\textbf{v}_x^{\theta} = ||\textbf{v}_x|| \cdot \cos{\theta} \cdot \textbf{i} = \textbf{v}_x \cdot \cos{\theta} = \textbf{k} \times \textbf{v} \times \textbf{k} \cdot \cos{\theta}
vxθ=∣∣vx∣∣⋅cosθ⋅i=vx⋅cosθ=k×v×k⋅cosθ
v
y
θ
=
∣
∣
v
x
∣
∣
⋅
sin
θ
⋅
j
=
∣
∣
v
∣
∣
⋅
sin
<
k
,
v
>
⋅
k
×
v
∣
∣
k
×
v
∣
∣
⋅
sin
θ
=
k
×
v
⋅
sin
θ
\textbf{v}_y^{\theta} = ||\textbf{v}_x|| \cdot \sin{\theta} \cdot \textbf{j} = ||\textbf{v}|| \cdot \sin<\textbf{k}, \textbf{v}> \cdot \frac{\textbf{k} \times \textbf{v}}{||\textbf{k} \times \textbf{v}||} \cdot \sin{\theta} = \textbf{k} \times \textbf{v} \cdot \sin{\theta}
vyθ=∣∣vx∣∣⋅sinθ⋅j=∣∣v∣∣⋅sin<k,v>⋅∣∣k×v∣∣k×v⋅sinθ=k×v⋅sinθ
因此,
v
θ
=
k
×
v
×
k
⋅
cos
θ
+
k
×
v
⋅
sin
θ
+
(
k
⋅
v
)
⋅
k
\textbf{v}^{\theta} = \textbf{k} \times \textbf{v} \times \textbf{k} \cdot \cos{\theta} + \textbf{k} \times \textbf{v} \cdot \sin{\theta} + (\textbf{k} \cdot \textbf{v}) \cdot \textbf{k}
vθ=k×v×k⋅cosθ+k×v⋅sinθ+(k⋅v)⋅k
另,由公式(
⋆
\star
⋆)
a
×
b
×
c
=
b
(
a
⋅
c
)
−
c
(
a
⋅
b
)
\textbf{a} \times \textbf{b} \times \textbf{c} = \textbf{b}(\textbf{a}\cdot\textbf{c})-\textbf{c}(\textbf{a}\cdot\textbf{b})
a×b×c=b(a⋅c)−c(a⋅b)可以得到:
v
θ
=
v
(
k
⋅
k
)
cos
θ
−
k
(
k
⋅
v
)
cos
θ
+
k
×
v
⋅
sin
θ
+
(
k
⋅
v
)
⋅
k
=
v
⋅
cos
θ
+
k
(
k
⋅
v
)
(
1
−
cos
θ
)
+
k
×
v
⋅
sin
θ
\textbf{v}^{\theta} = \textbf{v}(\textbf{k}\cdot\textbf{k})\cos\theta-\textbf{k}(\textbf{k}\cdot\textbf{v})\cos\theta + \textbf{k} \times \textbf{v} \cdot \sin{\theta} + (\textbf{k} \cdot \textbf{v}) \cdot \textbf{k} \newline \hspace{0.45cm} = \textbf{v}\cdot\cos\theta + \textbf{k}( \textbf{k}\cdot \textbf{v})(1-\cos\theta)+ \textbf{k}\times \textbf{v}\cdot\sin\theta
vθ=v(k⋅k)cosθ−k(k⋅v)cosθ+k×v⋅sinθ+(k⋅v)⋅k=v⋅cosθ+k(k⋅v)(1−cosθ)+k×v⋅sinθ
由此可以得到 R o d r i g u e s Rodrigues Rodrigues公式的结论。
\newline
\newline
第二部分:
R
o
d
r
i
g
u
e
s
Rodrigues
Rodrigues(罗德里格斯)公式的矩阵描述形式。
上述第一部分主要从原理上证明了,
R
o
d
r
i
g
u
e
s
Rodrigues
Rodrigues(罗德里格斯)公式的向量表述形式,在实际使用的时候,常用到的是矩阵形式的表述。事实上,矩阵形式的表述也是由向量形式经过展开和推导得来的,下面简单描述一下其中的过程。
首先将上述公式变形如下:
v
θ
=
v
⋅
cos
θ
+
k
(
k
⋅
v
)
(
1
−
cos
θ
)
+
k
×
v
⋅
sin
θ
=
v
−
v
+
v
⋅
cos
θ
+
k
(
k
⋅
v
)
(
1
−
cos
θ
)
+
k
×
v
⋅
sin
θ
=
v
−
(
1
−
cos
θ
)
v
+
(
1
−
cos
θ
)
(
k
⋅
v
)
k
+
sin
θ
⋅
k
×
v
=
v
+
(
1
−
cos
θ
)
(
(
k
⋅
v
)
k
−
v
)
+
sin
θ
⋅
k
×
v
=
v
+
(
1
−
cos
θ
)
(
(
k
⋅
v
)
k
−
v
(
k
⋅
k
)
)
+
sin
θ
⋅
k
×
v
\textbf{v}^{\theta} = \textbf{v}\cdot\cos\theta + \textbf{k}( \textbf{k}\cdot \textbf{v})(1-\cos\theta)+ \textbf{k}\times \textbf{v}\cdot\sin\theta \newline \hspace{0.45cm} = \textbf{v}-\textbf{v}+\textbf{v}\cdot\cos\theta + \textbf{k}( \textbf{k}\cdot \textbf{v})(1-\cos\theta)+ \textbf{k}\times \textbf{v}\cdot\sin\theta \newline \hspace{0.45cm} = \textbf{v} - (1-\cos\theta)\textbf{v} + (1-\cos\theta)(\textbf{k}\cdot \textbf{v})\textbf{k} + \sin\theta\cdot\textbf{k}\times\textbf{v} \newline \hspace{0.45cm} = \textbf{v} + (1-\cos\theta)((\textbf{k}\cdot\textbf{v})\textbf{k} - \textbf{v}) + \sin\theta\cdot\textbf{k}\times\textbf{v} \newline \hspace{0.45cm} = \textbf{v} + (1-\cos\theta)((\textbf{k}\cdot\textbf{v})\textbf{k} - \textbf{v}(\textbf{k}\cdot\textbf{k})) + \sin\theta\cdot\textbf{k}\times\textbf{v} \newline
vθ=v⋅cosθ+k(k⋅v)(1−cosθ)+k×v⋅sinθ=v−v+v⋅cosθ+k(k⋅v)(1−cosθ)+k×v⋅sinθ=v−(1−cosθ)v+(1−cosθ)(k⋅v)k+sinθ⋅k×v=v+(1−cosθ)((k⋅v)k−v)+sinθ⋅k×v=v+(1−cosθ)((k⋅v)k−v(k⋅k))+sinθ⋅k×v
由公式(
⋆
\star
⋆)
a
×
b
×
c
=
b
(
a
⋅
c
)
−
c
(
a
⋅
b
)
\textbf{a} \times \textbf{b} \times \textbf{c} = \textbf{b}(\textbf{a}\cdot\textbf{c})-\textbf{c}(\textbf{a}\cdot\textbf{b})
a×b×c=b(a⋅c)−c(a⋅b)可以得到:
v
θ
=
v
+
(
1
−
cos
θ
)
(
k
×
k
×
v
)
+
sin
θ
⋅
k
×
v
\textbf{v}^{\theta} = \textbf{v} + (1-\cos\theta)(\textbf{k}\times\textbf{k}\times\textbf{v}) + \sin\theta\cdot\textbf{k}\times\textbf{v}
vθ=v+(1−cosθ)(k×k×v)+sinθ⋅k×v
引入公式(
†
\dagger
†)
a
×
b
=
Ab
\textbf{a}\times\textbf{b}=\textbf{A}\textbf{b}
a×b=Ab,其中
a
\textbf{a}
a和
b
\textbf{b}
b是空间中的两个向量,
A
\textbf{A}
A是向量
a
\textbf{a}
a的“叉积矩阵”:
A
=
[
0
−
a
z
a
y
a
z
0
−
a
x
−
a
y
a
x
0
]
\textbf{A} = \left[ \begin{matrix} 0 & -a_z & a_y \\ a_z & 0 & -a_x \\ -a_y & a_x & 0 \\ \end{matrix} \right]
A=⎣⎡0az−ay−az0axay−ax0⎦⎤
因此,
k
×
v
=
Kv
\textbf{k}\times\textbf{v}=\textbf{K}\textbf{v}
k×v=Kv,其中
K
\textbf{K}
K是
k
\textbf{k}
k的“叉积矩阵”,则
k
×
k
×
v
=
K
2
v
\textbf{k}\times\textbf{k}\times\textbf{v} = \textbf{K}^2\textbf{v}
k×k×v=K2v
由此可以得到:
v
θ
=
v
+
(
1
−
cos
θ
)
(
k
×
k
×
v
)
+
sin
θ
⋅
k
×
v
=
v
+
(
1
−
cos
θ
)
⋅
K
2
v
+
sin
θ
⋅
Kv
=
Rv
\textbf{v}^{\theta} = \textbf{v} + (1-\cos\theta)(\textbf{k}\times\textbf{k}\times\textbf{v}) + \sin\theta\cdot\textbf{k}\times\textbf{v} \newline \hspace{0.45cm}=\textbf{v}+(1-\cos\theta)\cdot\textbf{K}^2\textbf{v}+ \sin\theta\cdot\textbf{K}\textbf{v} \newline \hspace{0.45cm}=\textbf{R}\textbf{v}
vθ=v+(1−cosθ)(k×k×v)+sinθ⋅k×v=v+(1−cosθ)⋅K2v+sinθ⋅Kv=Rv
其中:
R
=
I
+
K
sin
θ
+
K
2
(
1
−
cos
θ
)
\textbf{R}=\textbf{I}+\textbf{K}\sin\theta+\textbf{K}^2(1-\cos\theta)
R=I+Ksinθ+K2(1−cosθ)
则上述 v θ = v + sin θ ⋅ Kv + ( 1 − cos θ ) ⋅ K 2 v \textbf{v}^{\theta} = \textbf{v} + \sin\theta\cdot\textbf{K}\textbf{v} + (1-\cos\theta)\cdot\textbf{K}^2\textbf{v} vθ=v+sinθ⋅Kv+(1−cosθ)⋅K2v是矩阵描述形式。
\newline
\newline
第三部分:旋转矩阵与旋转向量的转化
由上述两个部分的阐述,可以得知,若一个空间矢量,围绕给定的方向轴旋转一个角度得到一个新的空间矢量,可以通过罗德里格斯公式来描绘,旋转前后两个矢量之间的相对关系。
由此可以设想,对于任意空间矢量
v
\textbf{v}
v,可以在笛卡尔坐标系下分别绕三个坐标轴
i
\textbf{i}
i,
j
\textbf{j}
j,
k
\textbf{k}
k旋转不同的角度:俯仰角
p
i
t
c
h
pitch
pitch,偏航角
y
a
w
yaw
yaw,翻滚角
r
o
l
l
roll
roll,则对于每一次相对单个坐标轴的旋转,都存在一个可以通过罗格里德斯公式来描述的旋转矩阵:
R
p
i
t
c
h
=
I
+
sin
θ
⋅
K
i
+
(
1
−
cos
θ
)
⋅
K
i
2
\textbf{R}_{pitch}=\textbf{I}+\sin\theta\cdot\textbf{K}_i+(1-\cos\theta)\cdot\textbf{K}_i^2
Rpitch=I+sinθ⋅Ki+(1−cosθ)⋅Ki2
R
y
a
w
=
I
+
sin
θ
⋅
K
j
+
(
1
−
cos
θ
)
⋅
K
j
2
\textbf{R}_{yaw}=\textbf{I}+\sin\theta\cdot\textbf{K}_j+(1-\cos\theta)\cdot\textbf{K}_j^2
Ryaw=I+sinθ⋅Kj+(1−cosθ)⋅Kj2
R
r
o
l
l
=
I
+
sin
θ
⋅
K
k
+
(
1
−
cos
θ
)
⋅
K
k
2
\textbf{R}_{roll}=\textbf{I}+\sin\theta\cdot\textbf{K}_k+(1-\cos\theta)\cdot\textbf{K}_k^2
Rroll=I+sinθ⋅Kk+(1−cosθ)⋅Kk2
则两个空间矢量间的矩阵
R
=
R
p
i
t
c
h
R
y
a
w
R
r
o
l
l
\textbf{R}=\textbf{R}_{pitch}\textbf{R}_{yaw}\textbf{R}_{roll}
R=RpitchRyawRroll。
由于空间平面可以由平面内的任意一点和平面的法向量唯一确定,则空间中两个法向量之间的关系,可以由罗德里格斯变换外加一个坐标系平移矢量联系起来时,则这两个平面也遵从相同的联系。这是在机器视觉中极为重要的应用。