1. 项目背景
电信行业是典型的数据密集型行业,只有正确地分析用户数据,发现更多商机,做出正确的决策,从而更好的向用户提供服务。电信行业的决策,在很大程度上依赖于客户的分类,针对不同类型的客户,实施相应的策略,从而获得客户的满意,征得客户的信任,把握真诚的客户群,最终是的企业自身获益。客户的分类依赖于客户价值的分析,本项目通过对客户价值的详细分析,并利用
CFSFDP 聚类算法,对客户进行类型的划分,可以获知客户价值的大小,客户价值的类型,从而得到客户的分类。
从客户需求出发,了解客户需要什么,他们有怎么样的特征,电信运营商为客户设置不同的优惠套餐,以争取更多的用户:推出不同的优惠套餐,降低客户流失率、提高收入、增加
ARPU 值(average revenue per user 每个用户平均收益),实现精准的市场营销策略定制。
2. 功能组成
基于 CFSFDP 聚类算法的电信客户价值分析的功能主要包括:
3. 数据读取与预处理
custinfo = pd.read_csv(‘custinfo.csv’)
custcall = pd.read_csv(‘custcall.csv’)
# 数据聚合:–对整个DataFrame数值求平均值,删除最后一列【month】
custcall2 = custcall.groupby(custcall[‘Customer_ID’]).mean()
custcall3 = custcall2.drop(‘month’, 1)
# 数据合并
data = pd.merge(custinfo,custcall3,left_on=‘Customer_ID’,right_index=True)
data.index = data[‘Customer_ID’]
data = data.drop(‘Customer_ID’,1)
# 数据探索:(mean,std,min,max,25%,50%,75%)
data.describe()
Columns| Gender| Age| L_O_S| Peak_calls| Peak_mins| OffPeak_calls|
OffPeak_mins| Weekend_calls| Weekend_mins| International_mins| Nat_call_cost
—|—|—|—|—|—|—|—|—|—|—|—
count| 18550.000000| 18550.000000| 18550.000000| 18550.000000| 18550.000000|
18550.000000| 18550.000000| 18550.000000| 18550.000000| 18550.000000|
18550.000000
mean| 0.482102| 31.506253| 33.710032| 39.756397| 118.768764| 17.356514|
51.603952| 2.790836| 8.356949| 28.292598| 2.944807
std| 0.499693| 12.848472| 14.093977| 39.677670| 84.289974| 16.120243|
33.003937| 2.836811| 6.097823| 23.488567| 4.593809
min| 0.000000| 12.000000| 9.533333| 0.000000| 0.000000| 0.000000| 0.000000|
0.000000| 0.000000| 0.001840| 0.000000
25%| 0.000000| 22.000000| 21.333333| 10.333333| 52.600000| 4.666667|
24.562500| 0.666667| 3.600000| 10.920083| 0.000000
50%| 0.000000| 30.000000| 33.666667| 26.833333| 101.100000| 12.333333|
48.350000| 1.833333| 7.316667| 22.397491| 1.000000
75%| 1.000000| 39.000000| 45.866667| 56.333333| 169.300000| 25.833333|
73.800000| 4.000000| 12.200000| 39.357374| 4.333333
max| 1.000000| 82.000000| 58.200000| 287.500000| 483.600000| 105.666667|
191.000000| 20.666667| 33.700000| 169.136422| 33.000000
4. 数据探索式分析
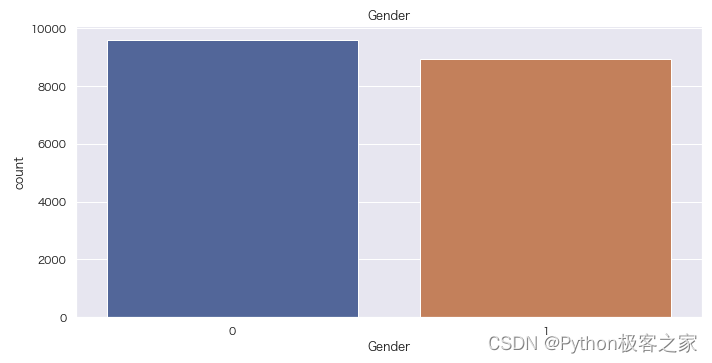
4.1 性别分布情况
fig = plt.figure(figsize=(10, 5))
sns.countplot(data[‘Gender’])
plt.title(‘Gender’)
plt.show()
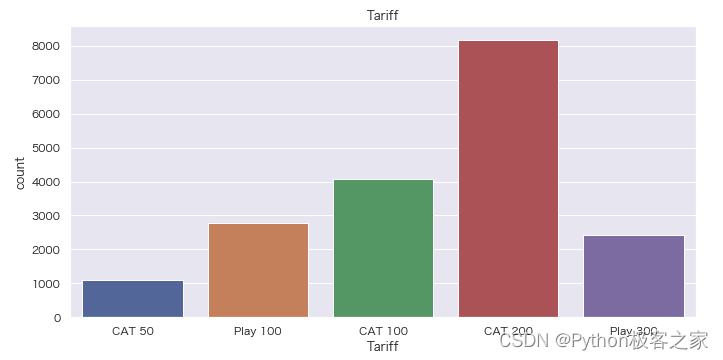
4.2 Tariff 分布情况
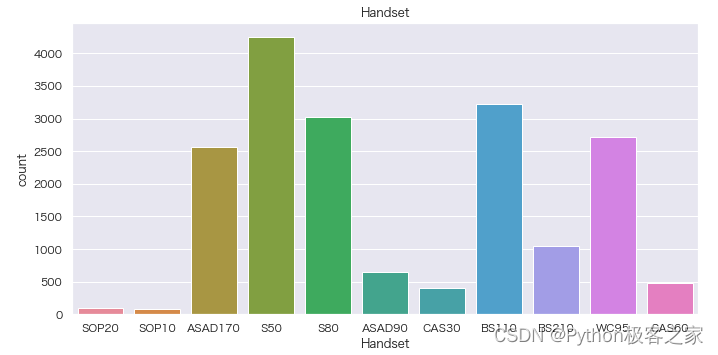
4.3 Handset 分布情况
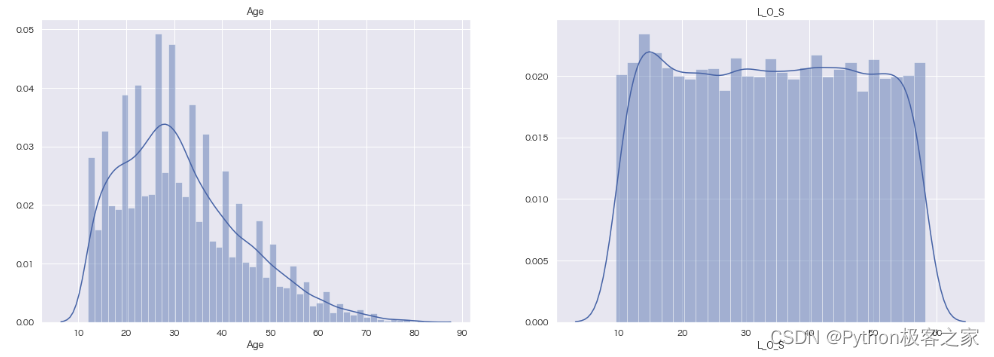
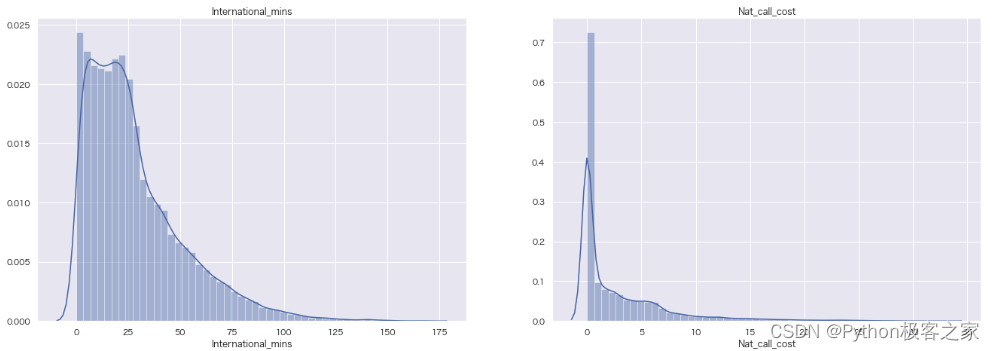
4.4 其他类别特征密度分布图
5. 特征工程
5.1 类别型的特征进行编码
encoder = LabelEncoder()
encoder = encoder.fit(data[‘Gender’])
data[‘Gender’] = encoder.transform(data[‘Gender’])
encoder = LabelEncoder()
encoder = encoder.fit(data[‘Tariff’])
data[‘Tariff’] = encoder.transform(data[‘Tariff’])
encoder = LabelEncoder()
encoder = encoder.fit(data[‘Handset’])
data[‘Handset’] = encoder.transform(data[‘Handset’])
5.2 数据标准化和数据降维
由于这些数据的特征可能都不在一个数量级,这就很难使用一些聚类算法进行分析,因此,我们需要使用sklearn中有关数据处理的算法MinMaxScaler(),对数据进行标准化,将数据缩放到0~1之间,以便聚类分析。
# 引入第三方库
from sklearn.preprocessing import MinMaxScaler
# 初始化MinMaxScaler()
min_max_model = MinMaxScaler()
# 使用数据进行拟合并转化
data = min_max_model.fit_transform(data)
6. 基于 CFSFDP 算法的电信客户价值聚类
6.1 CFSDP 聚类算法算法原理及实现
聚类分析又称聚类,是把一个数据集合划分为多个集群(cluster)的过程,使得相同集群内的数据之间具有相似性,不同集群的数据之间具有差异性。聚类是数据挖掘、统计分析的主要任务之一,应用于机器学习、模式识别、图像处理、信息检索、生物信息、数据压缩和计算机图像等领域。(From
维基百科)
常用的聚类算法包括:
(1)启发式分割算法:起始确定K个中心点,用距离公式来判断数据点归属,用代价函数(如最小化平方和)评价聚类结果,迭代直至最优,例如:K-Means,K-Medoids。
(2)基于模型的算法:起始随机确定若干个模型中心,用基于概率的方法判断数据点归属,通过迭代的方法找寻适合各个类的模型,例如:Gaussian Mixture
Model。
(3)降维的方法:通过降维,找寻数据间的特征,再完成聚类,例如:Spectral Clustering,Normalised-Cut。
(4)基于密度的方法:定义数据点密度,从少数对象开始拓展得到集群,例如:DBSCAN,CFSFDP。
CFSFDP算法即为Clustering by fast search and find of density peaks,这是由Alex
Rodriguez 和Alessandro
Laio于2014年发表在《Science》期刊的聚类算法。该算法的基本假设有两个,一是聚类中心附近的数据点具有较低的密度,二是数据点与其他密度更大的中心距离较远。

# 计算任意两点之间的欧氏距离,并存储为矩阵
def caldistance(v):
distance = np.zeros(shape=(len(v), len(v)))
for i in range(len(v)):
for j in range(len(v)):
if i > j:
distance[i][j] = distance[j][i]
elif i < j:
distance[i][j] = np.sqrt(np.sum(np.power(v[i] - v[j], 2)))
return distance
…
# 通过数距离小于dc的点的个数来衡量一个点的密度(离散型)**
def count_density(distance, dc):
density = np.zeros(shape=len(distance))
for index, node in enumerate(distance):
density[index] = len(node[node < dc])
return density
# 通过公式np.sum(np.exp(-(node / dc) ** 2))衡量一个店的密度(连续型)**
#node=dij
def continous_density(distance, dc):
density = np.zeros(shape=len(distance))
for index, node in enumerate(distance):
density[index] = np.sum(np.exp(-(node / dc) ** 2))
return density
# 计算密度大于自身的点中距离自己最近的距离以及该点的直属上级
def node_detal(density, distance):
detal_ls = np.zeros(shape=len(distance))
closest_leader = np.zeros(shape=len(distance), dtype=np.int32)
for index, node in enumerate(distance):
# 点密度大于当前点的点集合(一维数组)
density_larger_than_node = np.squeeze(np.argwhere(density > density[index]))
# 存在密度大于自己的点
if density_larger_than_node.size != 0:
…
return detal_ls, closest_leader
…
# 确定每点的最终分类
def clustering(closest_leader, chose_list):
for i in range(len(closest_leader)):
while closest_leader[i] not in chose_list:
j = closest_leader[i]
closest_leader[i] = closest_leader[j]
new_class = closest_leader[:]
return new_class # new_class[i]表示第i点所属最终分类
6.2 聚类结果可视化
def show_result(new_class, norm_data, chose_list):
colors = [
‘#FF0000’, ‘#FFA500’, ‘#FFFF00’, ‘#00FF00’, ‘#228B22’,
‘#0000FF’, ‘#FF1493’, ‘#EE82EE’, ‘#000000’, ‘#FFA500’,
‘#00FF00’, ‘#006400’, ‘#00FFFF’, ‘#0000FF’, ‘#FFFACD’,
‘#770077’, ‘#008866’, ‘#000088’, ‘#9F88FF’,‘#3A0088’,
‘#660077’, ‘#FF00FF’,‘#0066FF’, ‘#00FF00’, ‘#7744FF’,
‘#33FFDD’, ‘#CC6600’, ‘#886600’, ‘#227700’, ‘#008888’,
‘#FFFF77’, ‘#D1BBFF’
]
# 画最终聚类效果图
leader_color = {}
main_leaders = dict(collections.Counter(new_class)).keys()
for index, i in enumerate(main_leaders):
leader_color[i] = index
plt.figure(num=3, figsize=(15, 15))
for node, class_ in enumerate(new_class):
# 标出每一类的聚类中心点
if node in chose_list:
plt.scatter(x=norm_data[node, 0], y=norm_data[node, 1], marker=‘*’, s=500, c=‘black’,alpha=1)
else:
plt.scatter(x=norm_data[node, 0], y=norm_data[node, 1], c=colors[leader_color[class_]], s=100, marker=‘o’,alpha=1)
plt.title(‘The Result Of Cluster’)
plt.show()
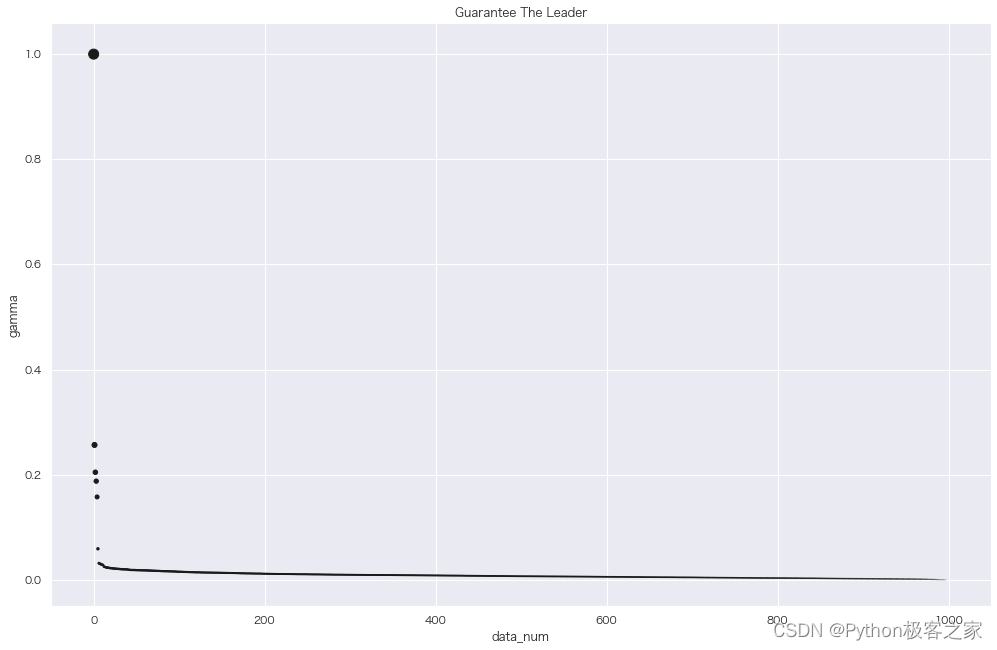
# 画detal图和原始数据图
def show_optionmal(den, det, v):
plt.figure(num=1, figsize=(15, 9))
ax1 = plt.subplot(121)
for i in range(len(v)):
plt.scatter(x=den[i], y=det[i], c=‘k’, marker=‘o’, s=15)
plt.xlabel(‘Density’)
plt.ylabel(‘Detal’)
plt.title(‘Chose Leader’)
plt.sca(ax1)
ax2 = plt.subplot(122)
for j in range(len(v)):
plt.scatter(x=v[j, 0], y=v[j, 1], marker=‘o’, c=‘k’, s=15)
plt.xlabel(‘axis_x’)
plt.ylabel(‘axis_y’)
plt.title(‘Dataset’)
plt.sca(ax2)
plt.show()
项目分享
项目分享:
https://gitee.com/asoonis/feed-neo