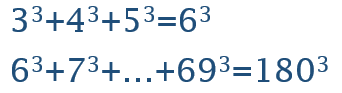1.题目

编写一个应用程序，验证以下等式是成立的：

提示：if分支语句、for循环语句与C、C++是一样的。

如果能完成上面的验证，则达到基本要求（可得到基本分数8分）。

较高要求，可根据实际情况选做(可得到附加的2分）：找到更多的这样的整数：一些相续正整数的立方和正好等于另一个整数的立方。

2.题解

验证不等式是否成立，直接按照题目要求编写即可；

扩展要求：设定最大值数量为300，直接建立循环，搜索连续正整数的立方和是否可以开立方，如果可以开立方，则输出相关结果。

public class homework1 {
    public static void main(String[] args){

        // 验证两个等式
        int sum=0;
        for(int i=3; i<=5; i++){
            sum += i*i*i;
        }
        if(sum == 6*6*6)
            System.out.println("3^3+4^3+5^3==6^3");
        else
            System.out.println("3^3+4^3+5^3!=6^3");

        sum = 0;
        for(int i=6; i<=69; i++){
            sum += i*i*i;
        }
        if(sum == 180*180*180)
            System.out.println("6^3+7^3+...+69^3==180^3");
        else
            System.out.println("6^3+7^3+...+69^3!=180^3");

        // 找到更多的数
        int max_num = 300;
        int[] list = new int[max_num+1];
        for(int i=1;i<=max_num;i++)
            list[i]=i*i*i;
        sum = 0;
        for(;max_num>=2;max_num--)
        {
            for(int i=1;i<max_num;i++)
            {
                for(int k=i;k<=max_num;k++)
                {
                    sum+=list[k];
                }
                if(Math.cbrt(sum)==(int)Math.cbrt(sum))
                {
                    for(int k=i;k<max_num;k++)
                    {
                        System.out.print(k+"^3 + ");
                    }
                    System.out.print(max_num +"^3 = "+ (int)Math.cbrt(sum) +"^3");
                    System.out.println();
                    sum=0;
                }
                else
                    sum=0;
            }
        }
    }
}