回文问题
目录
1、简介
对于一个给定的字符串,如果它的正序和倒序是相同的,则称这样的字符串为 回文。
例如,对于字符串 “aabaa”,它的倒序也为 “aabaa”,因此它是一个回文;对于字符串 “abba”,它的倒序也为 “abba”,因此它也是一个回文;对于字符串 “abbc”,它的倒序为 “cbba”,因此它不是一个回文。
从回文的定义可以看出,回文总是 关于中心对称 的。
2、经典的回文问题
(1) 判断一个字符串是否为回文
根据回文的定义可以知道回文是一个关于中心对称的字符串。那么要判断一个字符串是否为回文,最简单的办法就是定义两个指针 l l l 和 r r r 分别从字符串的首尾向字符串中心进行扫描。在扫描过程中,一旦存在两个字符不相同,则说明这个字符串是不是回文;否则,这个扫描过程会一直进行下去直到两个指针相遇,在这情况下说明当前字符串是一个回文。
根据这样的思路,可以得到判断字符串是否为回文的代码如下:
// 判断字符串 s 是否为回文
bool isPalindrome(const string &s) {
int l = 0, r = s.length() - 1;
while(l < r && s[l] == s[r]){
l++;
r--;
}
if(l < r) return false;
else return true;
}
复杂度分析
时间复杂度: O ( n ) O(n) O(n)。
空间复杂度: O ( 1 ) O(1) O(1)。
(2) 给定字符集求构建的最长回文长度
给定一个包含大写字母和小写字母的字符串 s s s ,返回由这些字符构造的最长的回文长度。例如,对于给定的字符串 “abccccdd”,能够构建的最长的回文为 “dccaccd”(或 “dccbccd” 等),其长度为 7。
对应题目:LeetCode.409 最长回文串。
分析
这道题乍一看会觉得无从下手,但想通之后会发现很简单。
还是从回文的性质出发,由于回文是关于中心对称的。因此,所有回文总是满足以下两个条件之一:
- 若当前回文长度为偶数,则所有字符都将出现偶数次;
- 若当前回文长度为奇数,则位于中心位置的字符将出现奇数次,其余所有字符都将出现偶数次;
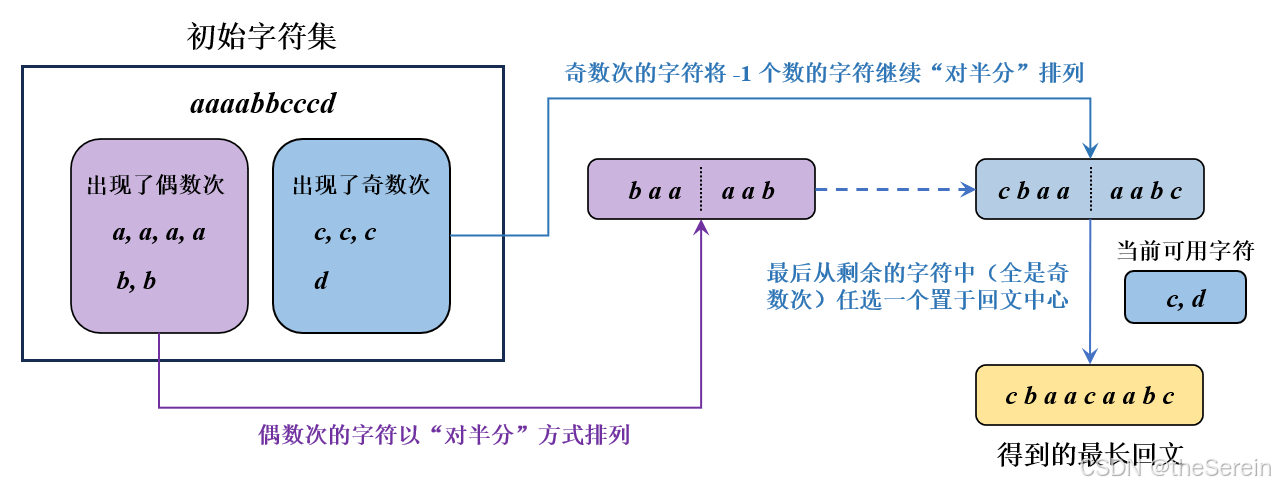
基于此,从贪心的角度出发,要使构建的回文长度最长,可以把所有出现偶数次的字符都选中。在这基础上,如果还有奇数次的字符(假设出现次数为 t t t),则将这些字符中的 t − 1 t-1 t−1 个偶数次字符也选中,并在最后再选择一个出现次数为奇数次的字符位于回文中心。下图展示了该思路的具体执行流程:
对应代码:
#include<unordered_map>
using namespace std;
// 给定字符集求构建的最长回文长度
int longestPalindrome(const string &s)
{
unordered_map<char, int> mp;
int slen = s.length();
int cnt = 0, tmp, odd = 0;
// 统计各字符的出现次数
for (int i = 0; i < slen; i++)
mp[s[i]]++;
// 遍历字典,偶数的字符全部都可用,奇数的只能用 - 1 个数的字符
for (const auto &pair : mp)
{
tmp = pair.second;
cnt += (tmp - (tmp&1));
// 标记是否存在奇数个数的字符
if (tmp & 1) odd = 1;
}
return cnt + odd;
}
复杂度分析
时间复杂度: O ( n ) O(n) O(n)。
空间复杂度: O ( n ) O(n) O(n)。
(3) 求最长回文子串
给定一个字符串 s s s,求 s s s 中的最长回文子串。例如,对于字符串 “cbbd”,其中的最长回文子串为 “bb”;对于字符串 “aasabasa”,其中的最长回文子串为 “asabasa”。
对应题目:LeetCode.5 最长回文子串。
分析
最简单直接的办法就是枚举,即枚举所有子串,然后依次判断当前子串是否为一个回文,如果是就记录当前回文串的长度,并维护更新一个用于记录最大回文长度的变量(和对应位置)。枚举结束时,便可以基于维护的相关变量输出最长的回文子串。对于一个字符串 s s s,枚举其子串的代码如下:
// 双重循环枚举字符串 s 的全部子串
int slen = s.length();
for(int l=0; l<slen; l++)
for(int r=l; r<slen; r++){
string substr = s.substr(l, r-l+1);
/* 判断 substr 是否为回文的代码 */
}
这个枚举过程是 O ( n 2 ) O(n^2) O(n2) 的时间复杂度。对于每个子串,还需要判断其是否为回文( O ( n ) O(n) O(n) 的时间复杂度)。因此,该方法最终的时间复杂度为 O ( n 3 ) O(n^3) O(n3),是不能容忍的。因此,这个方法不可取。
方法一:中心拓展
注意到回文是一个对称结构,因此我们可以考虑这样的一种枚举方式:遍历每个字符串并将其作为回文中心,在此基础上再向两侧拓展以寻找当前回文中心的最长边界。在这个过程中,每次都维护更新一个用于记录最大回文长度的变量(和对应位置),遍历结束后便能得到最长的回文子串。在这个枚举方案中,遍历原始字符串的时间复杂度为 O ( n ) O(n) O(n),向两侧拓展寻找回文中心的最长边界的时间复杂度也为 O ( n ) O(n) O(n)。因此,中心拓展方法的时间复杂度为 O ( n 2 ) O(n^2) O(n2)。
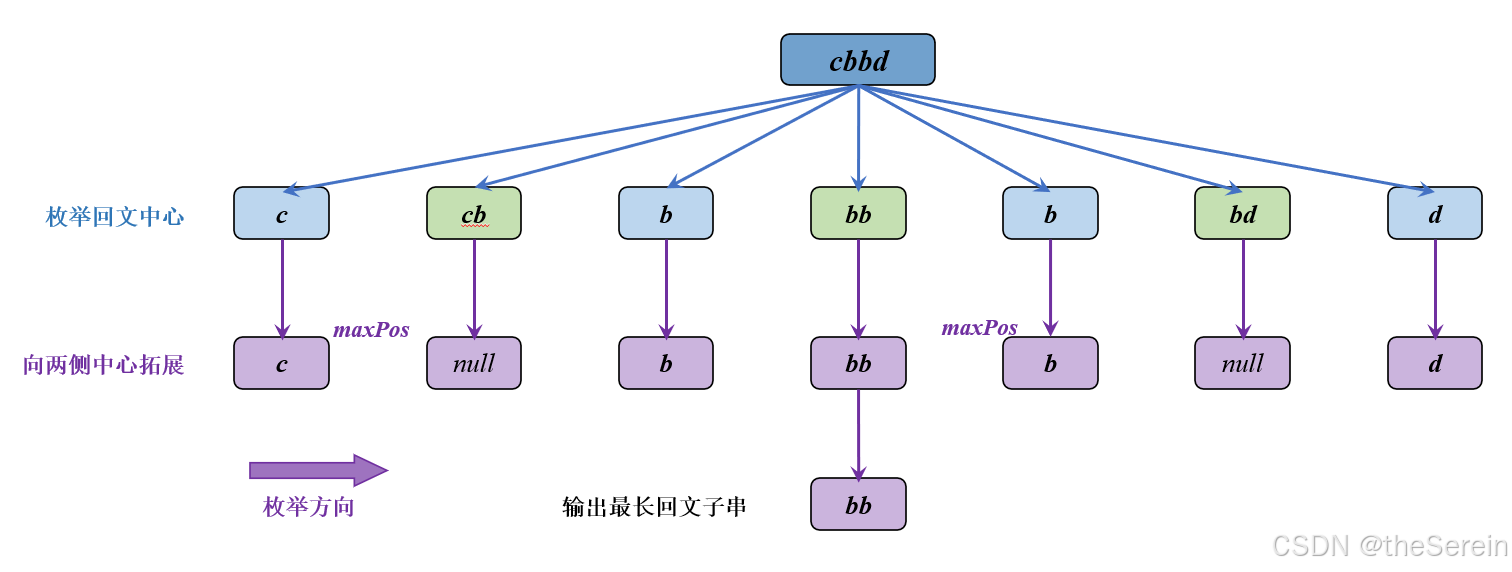
具体实现时,需要处理一个问题:如何有序地枚举所有回文中心?之所以有这个问题,是因为回文需要分长度为奇数和长度为偶数的两种情况。如果回文长度是奇数,那么回文中心是一个字符;如果回文长度是偶数,那么中心是两个字符。对于某个字符串 “abcbd”,它的回文中心有以下两种划分方式:
- 回文中心为单字符,即 “a”、“b”、“c”、“b”、“d”,亦即原字符串本身的长度, n n n;
- 回文中心为双字符,即 “ab”、“bc”、“cb”、“bd”,亦即原字符串本身的长度再减 1, n − 1 n-1 n−1;
因此,对长度为 n n n 的字符串 s s s,我们需要枚举的回文中心有 n + ( n − 1 ) = 2 n − 1 n+(n-1)=2n-1 n+(n−1)=2n−1 种情况。
中心拓展的思路如下:
对应代码:
// 给定字符串,求最长的回文子串
string longestPalindrome(const string &s)
{
// longestPd 记录最长的回文子串长度,posPd 记录对应最长子串的起始位置
int slen = s.size(), longestPd = 0, posPd;
int l, r, lenPd;
for (int i = 0, maxIter = 2 * slen - 1; i < maxIter; i++)
{
// 确定当前的回文中心
l = i / 2, r = i / 2 + (i & 1);
// 寻找当前回文中心的最长边界
while (l >= 0 && r < slen && s[l] == s[r])
l--, r++;
// 计算当前回文的长度
lenPd = r - l - 1;
// 更新
if (lenPd > longestPd)
{
longestPd = lenPd;
posPd = l + 1;
}
}
return s.substr(posPd, longestPd);
}
复杂度分析
时间复杂度: O ( n 2 ) O(n^2) O(n2)。
空间复杂度: O ( n ) O(n) O(n)。
方法二:Manacher 算法
Manacher 算法是一种在线性时间内求解最长回文子串的算法。
Manacher 算法也会面临「方法一」中的奇数长度和偶数长度的问题,它的处理方式是在所有的相邻字符中间(以及字符串的首尾位置)插入 #,比如 “abaa” 会被处理成 “#a#b#a#a#”,这样可以保证所有找到的回文串都是奇数长度的,亦即所有的回文都是以单字符为中心的。在下面的谈论中,我们用 s s s 表示添加了 “#” 的新字符串。
在学习 Manacher 算法之前,需要先了解以下定义。
回文半径 RL:回文中最左(或最右)位置的字符与其对称轴之间的字符数量称为回文半径(包含对称轴本身),我们用 R L RL RL 表示。因此,对字符串 s s s 中的某个字符 s [ i ] s[i] s[i] 而言,我们可以用数组 R L [ i ] RL[i] RL[i] 表示以字符 s [ i ] s[i] s[i] 为回文中心得到的回文半径。例如,对于字符串 “aba” 和字符串 “abba” 有以下定义:
位置: 0 1 2 3 4 5 6
字符: # a # b # a #
RL: 1 2 1 4 1 2 1
RL-1: 0 1 0 3 0 1 0
位置: 0 1 2 3 4 5 6 7 8
字符: # a # b # b # a #
RL: 1 2 1 2 5 2 1 2 1
RL-1: 0 1 0 1 4 1 0 1 0
对字符串 “#a#b#a#” 而言,第一个字符 “a” 的回文半径为 2(子串 “#a#” 构成一个回文,最左侧的 “#” 到 “a” 共计 2 个字符 “#a”),因此 R L [ 1 ] = 2 RL[1]=2 RL[1]=2。
对字符串 “#a#b#b#a#” 而言,正中间的字符 “#” 的回文半径为 5(整个字符串 “#a#b#b#a#” 构成一个回文,最左侧的 “#” 到正中间 “a” 共计 5 个字符 “#a#b#”),因此 R L [ 4 ] = 5 RL[4]=5 RL[4]=5。
注意到在上面给出的例子中我们还给出了 R L − 1 RL-1 RL−1(实际上就是 “最左(或最右)位置的字符与其对称轴之间的字符数(不包含对称轴本身)”),可以发现,各 R L [ i ] − 1 RL[i]-1 RL[i]−1 的值恰好等于在原字符串中以字符 s [ i ] s[i] s[i] 为对称轴的回文长度。例如,在字符串 “#a#b#a#” 中, R L [ 3 ] − 1 = 3 RL[3]-1=3 RL[3]−1=3,恰好等于原始字符串 “aba” 以字符 b b b 为回文中心得到的最长回文长度。在字符串 “#a#b#b#a#” 中, R L [ 4 ] − 1 = 4 RL[4]-1=4 RL[4]−1=4,恰好等于原始字符串 “abba” 以字符 b b bb bb 为回文中心得到的最长回文长度(“#” 是插入的字符,可以理解为一个虚拟字符。如果处理 R L [ i ] RL[i] RL[i] 时对应的 s [ i ] s[i] s[i] 是虚拟字符,它对应在原字符串中的回文中心就是以 s [ i ] s[i] s[i] 前后两个字符组成的双字符)。
另一方面,由于回文是对称的,因此对于任意的 R L [ i ] RL[i] RL[i] 都有这样的一个性质: i − R L [ i ] + 1 2 = \frac{i-RL[i]+1}{2}= 2i−RL[i]+1=以字符 s [ i ] s[i] s[i] 为回文中心构成的最长回文在原字符串中的起始位置。例如,在字符串 “#a#b#a#” 中, 3 − R L [ 3 ] + 1 2 = 0 \frac{3-RL[3]+1}{2}=0 23−RL[3]+1=0,而在原始字符串 “aba” 中,以字符 “b” 为回文中心的起始索引也是 0;在字符串 “#a#b#b#a#” 中, 4 − R L [ 4 ] + 1 2 = 0 \frac{4-RL[4]+1}{2}=0 24−RL[4]+1=0,而在原始字符串 “abba” 中,以字符 “bb” 为回文中心的起始索引也是 0。
在熟悉以上概念后,“求最长回文子串” 的任务就被转换为 “求 R L RL RL 数组”。更准确地说,是在线性时间复杂度内求 R L RL RL 数组。Manacher 算法计算 R L RL RL 数组的整体流程和中心拓展方法是一致的:(1) 遍历字符串 s s s(假设遍历指针为 i i i);(2) 计算以各字符 s [ i ] s[i] s[i] 为回文中心的回文半径(即 R L [ i ] RL[i] RL[i])。与中心拓展方法不同的是,Manacher 算法充分利用了回文 中心对称 的特性,进而大幅降低了许多重复计算。
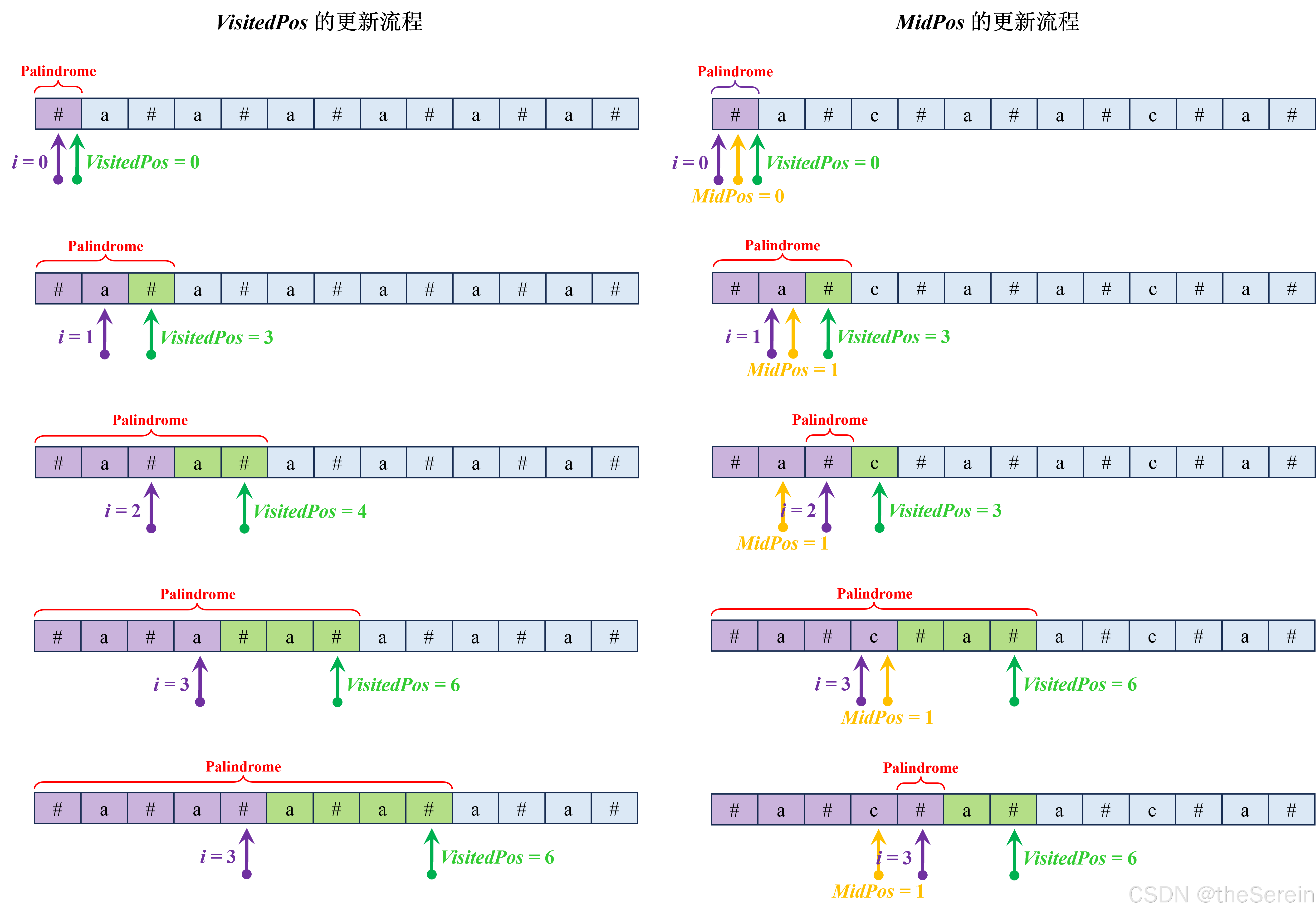
最远已访问指针 VisitedPos:在计算以字符 s [ i ] s[i] s[i] 为回文中心的回文半径时,我们定义 “沿着与遍历方向一致的被访问的最远位置为 V i s i t e d P o s VisitedPos VisitedPos”。这就是说, V i s i t e d P o s VisitedPos VisitedPos 指示了在更新 R L RL RL 数组时,被访问到的最远位置。
最远已访问指针对应的回文中心指针 MidPos:为便于相关参数的计算,还需要定义最远已访问指针 V i s i t e d P o s VisitedPos VisitedPos 对应的回文中心位置 M i d P o s MidPos MidPos,显然, M i d P o s = ⌊ V i s i t e d P o s 2 ⌋ MidPos=\left\lfloor\frac{VisitedPos}{2}\right\rfloor MidPos=⌊2VisitedPos⌋。
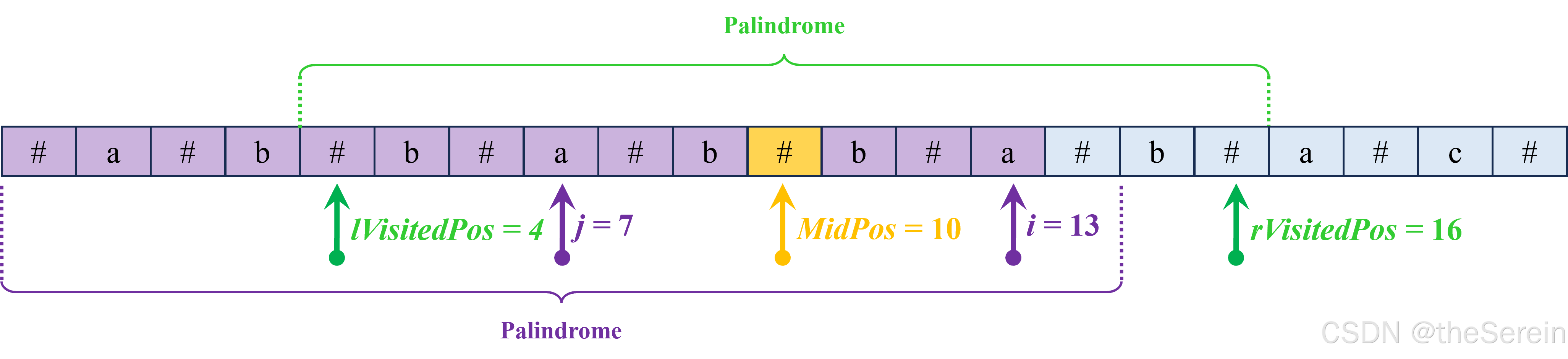
下图给出了 V i s i t e d P o s VisitedPos VisitedPos 和 M i d P o s MidPos MidPos 的具体更新步骤:
关于 V i s i t e d P o s VisitedPos VisitedPos 和 M i d P o s MidPos MidPos,需要注意以下两个关键点:
- V i s i t e d P o s ≥ i VisitedPos \geq i VisitedPos≥i。最远已访问指针 V i s i t e d P o s VisitedPos VisitedPos 始终不小于遍历指针 i i i。
- i ≥ M i d P o s i \geq MidPos i≥MidPos。理想情况下,每次中心拓展 V i s i t e d P o s VisitedPos VisitedPos 都进行了更新,则 i = ⌊ V i s i t e d 2 ⌋ = M i d P o s i=\left\lfloor\frac{Visited}{2}\right\rfloor=MidPos i=⌊2Visited⌋=MidPos;其他情况下, V i s i t e d P o s VisitedPos VisitedPos 未被更新,则 i = i + 1 i = i+1 i=i+1 而 M i d P o s MidPos MidPos 不发生变化,因此有 i > M i d P o s i>MidPos i>MidPos。综上, i ≥ M i d P o s i \geq MidPos i≥MidPos。
下面正式进入核心环节:Manacher 算法如何将 R L RL RL 数组的求解降低至线性时间复杂度的。
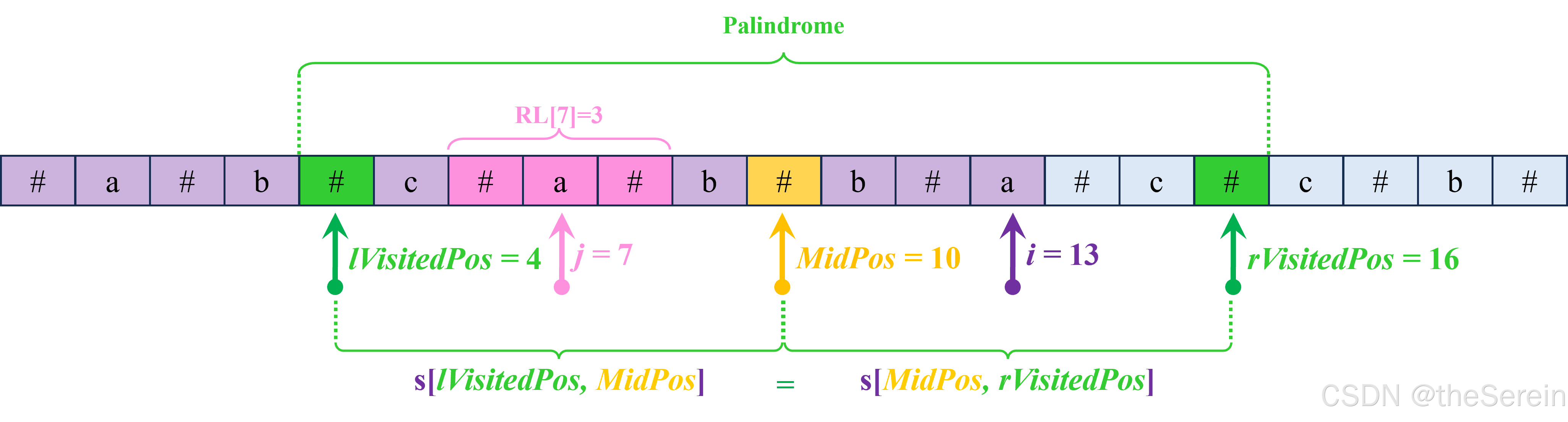
首先要明确一点:由 V i s i t e d P o s VisitedPos VisitedPos 和 M i d P o s MidPos MidPos 共同指示的回文是一个关于 M i d P o s MidPos MidPos 对称的字符串。例如,在下图中,字符串 s [ l V i s i t e d P o s , M i d P o s ] s[lVisitedPos, MidPos] s[lVisitedPos,MidPos] 和 s [ M i d P o s , r V i s i t e d P o s ] s[MidPos, rVisitedPos] s[MidPos,rVisitedPos] 完全一致。
在这情况下,当我们计算以 s [ 13 ] s[13] s[13] 为回文中心的回文半径 R L [ 13 ] RL[13] RL[13] 时,就不需要再执行一次中心拓展过程,因为 s [ 13 ] s[13] s[13] 和 s [ 7 ] s[7] s[7] 关于 M i d P o s = 10 MidPos=10 MidPos=10 对称,而 R L [ 7 ] RL[7] RL[7] 在之前已经计算过了,所以可以确定 R L [ 13 ] RL[13] RL[13] 的下限,即 R L [ 13 ] ≥ R L [ 7 ] = 3 RL[13]\geq RL[7]=3 RL[13]≥RL[7]=3,然后在这基础上再对 R L [ 13 ] RL[13] RL[13] 进行中心拓展。这样一来,就大幅降低了计算 R L [ 13 ] RL[13] RL[13] 的开销。注:根据对称法则 i i i、 j j j 和 M i d P o s MidPos MidPos 存在关系 i + j = 2 ∗ M i d P o s i+j=2*MidPos i+j=2∗MidPos,即 j = 2 ∗ M i d P o s − i j=2*MidPos-i j=2∗MidPos−i。
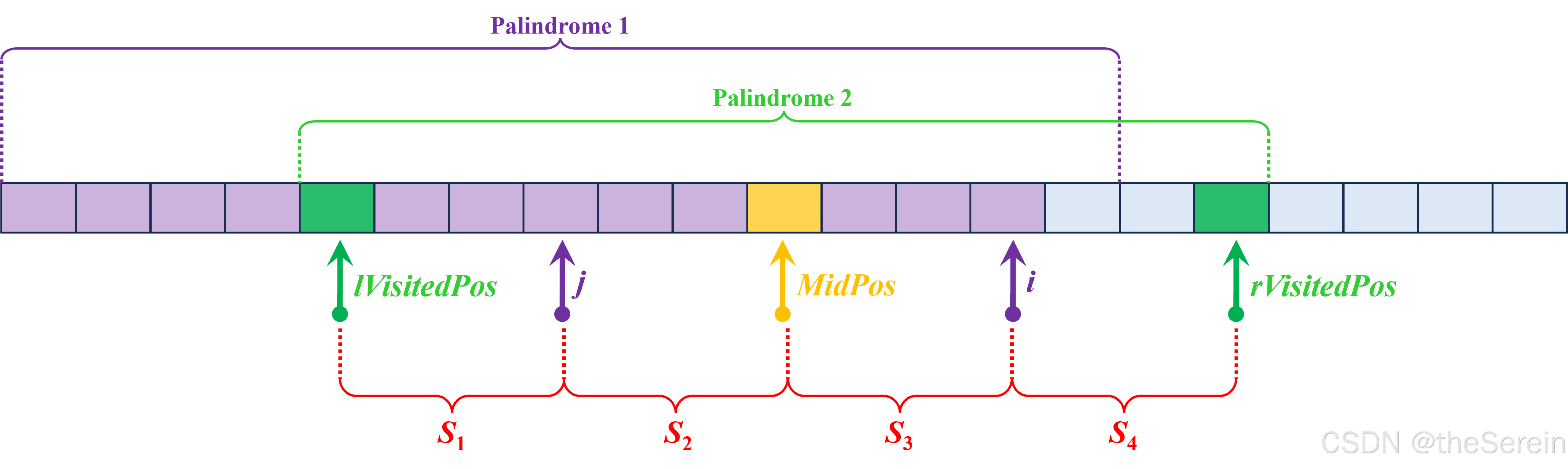
但是,直接取 R L [ 13 ] ≥ R L [ 7 ] RL[13]\geq RL[7] RL[13]≥RL[7] 是不准确的。考虑一种情况:以 s [ 7 ] s[7] s[7] 为回文中心的半径长度超过了 l V i s i t e d P o s lVisitedPos lVisitedPos 指示的位置,如下图所示。
在这种情况下,由于以 M i d P o s MidPos MidPos 为回文中心的回文仅能保证子串 s [ l V i s i t e d P o s , M i d P o s ] s[lVisitedPos, MidPos] s[lVisitedPos,MidPos] 和 s [ M i d P o s , r V i s i t e d P o s ] s[MidPos, rVisitedPos] s[MidPos,rVisitedPos] 一致,而无法保证在超出这个范围以外的部分也相同。此时, R L [ i ] RL[i] RL[i] 的下限又该如何确定呢?这时候,就需要从回文 中心对称 的特性出发进行思考了,观察下图:
证明:字符串 S 3 S_3 S3 和 S 4 S_4 S4 关于 i i i 对称
因为 回文 P a l i n d r o m e 1 Palindrome1 Palindrome1 关于 j j j 对称
所以 字符串 S 1 S_1 S1 和 S 2 S_2 S2 关于 j j j 对称
因为 回文 P a l i n d r o m e 2 Palindrome2 Palindrome2 关于 M i d P o s MidPos MidPos 对称
所以 字符串 S 2 S_2 S2 和 S 3 S_3 S3 关于 M i d P o s MidPos MidPos 对称
由于 S 1 S_1 S1 和 S 2 S_2 S2 关于 j j j 对称, S 2 S_2 S2 和 S 3 S_3 S3 关于 M i d P o s MidPos MidPos 对称
所以 字符串 S 1 = S 3 S_1 = S_3 S1=S3
又因为 回文 P a l i n d r o m e 2 Palindrome2 Palindrome2 关于 M i d P o s MidPos MidPos 对称
所以 字符串 S 1 S_1 S1 和 S 4 S_4 S4 关于 M i d P o s MidPos MidPos 对称
综合 S 1 = S 3 S_1 = S_3 S1=S3 可知, S 3 S_3 S3 和 S 4 S_4 S4 关于 M i d P o s MidPos MidPos 对称
因此,当以 s [ j ] s[j] s[j] 为中心的回文范围超出了 l V i s i t e d P o s lVisitedPos lVisitedPos 时,我们可以确定字符 s [ i ] s[i] s[i] 的回文半径不低于 V i s i t e d P o s − i + 1 VisitedPos-i+1 VisitedPos−i+1,即 R L [ i ] ≥ ( r V i s i t e d P o s − i + 1 ) RL[i] \geq (rVisitedPos-i+1) RL[i]≥(rVisitedPos−i+1)。
综上,可以将字符 s [ i ] s[i] s[i] 的回文半径 R L [ i ] RL[i] RL[i] 的初始化归结为以下 3 种情况:
- i = V i s i t e d P o s i = VisitedPos i=VisitedPos :说明以 i i i 为中心的回文还没有任何一个部分被访问过,这种情况下只能从 i i i 的左右两边进行中心扩展,即初始化 R L [ i ] = 1 RL[i]=1 RL[i]=1。
-
i
<
V
i
s
i
t
e
d
P
o
s
i < VisitedPos
i<VisitedPos:
- R L [ j ] ≤ ( V i s i t e d P o s − i ) RL[j] \leq (VisitedPos-i) RL[j]≤(VisitedPos−i) 时(以 i i i 的对称位置 j j j 为中心的回文未超过 V i s i t e d P o s VisitedPos VisitedPos 对应回文的范围),初始化 R L [ i ] = R [ j ] RL[i]=R[j] RL[i]=R[j]。
- R L [ j ] > ( V i s i t e d P o s − i ) RL[j] >(VisitedPos-i) RL[j]>(VisitedPos−i) 时(以 i i i 的对称位置 j j j 为中心的回文超过了 V i s i t e d P o s VisitedPos VisitedPos 对应回文的范围),初始化 R L [ i ] = V i s i t e d P o s − i RL[i]=VisitedPos-i RL[i]=VisitedPos−i。
以上便是 Manacher 算法的核心思路,在寻找最长的回文子串时,还需要额外引入一个变量来记录当前找到的最长回文长度。可能你会疑惑:确定了最长回文长度,还需要一个变量保存这个回文对应的起点(或者中心位置)才能得到对应的回文串?实际上并不需要。还记得么,前面我们曾说过,在对原始字符串插入 “#” 后,各 R L RL RL 通过 i − R L [ i ] + 1 2 \frac{i-RL[i]+1}{2} 2i−RL[i]+1 便可以得到该回文对应的起点索引。
于是,可以写出 Manacher 算法的完整代码如下:
string longestPalindromeStr(const string &s)
{
// 预处理(填充 “#”)
string s_;
for (int i = 0, slen = s.length(); i < slen; i++)
{
s_ += "#";
s_ += s[i];
}
s_ += "#";
// 寻找最长回文子串
int slen = s_.size(), visitedPos = 0, midPos = 0, maxRLPos = 0;
vector<int> RL(slen, 0);
for (int i = 0; i < slen; i++)
{
// 当前遍历字符的位置位于 visitedPos 之前
if (i < visitedPos)
RL[i] = min(RL[2 * midPos - i], visitedPos - i + 1);
// 当前遍历字符的位置与 visitedPos 重合
else
RL[i] = 1;
// 中心拓展(注意处理边界)
while (i - RL[i] >= 0 && i + RL[i] < slen && s_[i - RL[i]] == s_[i + RL[i]])
RL[i] += 1;
// 更新 visitedPos 和 midPos
if (i + RL[i] - 1 > visitedPos)
{
visitedPos = RL[i];
midPos = i;
}
// 更新 maxRL
if (RL[i] > RL[maxRLPos])
maxRLPos = i;
}
return s.substr((maxRLPos - RL[maxRLPos] + 1) / 2, RL[maxRLPos] - 1);
}
复杂度分析
时间复杂度: O ( n ) O(n) O(n)。
空间复杂度: O ( n ) O(n) O(n)。
(4) 求回文子串的数目
给定一个字符串 s s s,求 s s s 中全部的回文子串数目。例如,对于字符串 “abc”,其中的回文子串有 “a”、“b”、“c” 共 3 个,因此返回 3;对于字符串 “aba”,其中的回文子串有 “a”、“b”、“c” 、“aba” 共 4 个,因此返回 4。
对应题目:LeetCode.647 回文子串。
分析
方法一:中心拓展
可以利用中心拓展方式枚举全部的回文子串,并进行统计,对应代码如下:
int countSubstrings(string s)
{
int slen = s.size(), count = 0;
int l, r;
for (int i = 0, maxIter = 2 * slen - 1; i < maxIter; i++)
{
// 确定当前的回文中心
l = i / 2, r = i / 2 + (i & 1);
// 枚举以当前字符为中心的全部回文
while (l >= 0 && r < n && s[l] == s[r])
{
--l;
++r;
++count;
}
}
return count;
}
复杂度分析
时间复杂度: O ( n 2 ) O(n^2) O(n2)。
空间复杂度: O ( 1 ) O(1) O(1)。
方法二:Manacher 算法
从前面的分析知道, Manacher 算法可以在线性时间复杂度度内求出全部的 R L [ i ] RL[i] RL[i](即所有字符的最长回文半径),这实际上就已经枚举了所有的回文。那么,要统计给定字符的全部回文子串,就只需要在 Manacher 算法内部进行累加即可。
需要注意的是,由于对字符串添加了 “#”,就需要对这些字符进行排除。如何排除呢?
很简单,注意到在添加 “#” 后,所有的回文都是以单字符为中心的,在这种情况下,所有原本是双字符为中心的回文(对应在新串中为 “#”)的最小 R L [ i ] RL[i] RL[i] 为 3;所有单字符为中心的回文的最小 R L [ i ] RL[i] RL[i] 也为 3;而对于无效的 “#” 符的 R L [ i ] RL[i] RL[i] 值就只能取到 1。因此,对所有的 R L [ i ] RL[i] RL[i],其真实贡献可以取 R L [ i ] − 1 2 \frac{RL[i]-1}{2} 2RL[i]−1,这样一来,就消除了 “#” 对真实结果的影响。
下面给出利用 Manacher 算法求解该问题的完整代码:
int countSubstrings(const string &s)
{
// 预处理(填充 “#”)
string s_;
for (int i = 0, slen = s.length(); i < slen; i++)
{
s_ += "#";
s_ += s[i];
}
s_ += "#";
// 统计回文子串个数
int slen = s_.size(), visitedPos = 0, midPos = 0, count = 0;
vector<int> RL(slen, 0);
for (int i = 0; i < slen; i++)
{
// 当前遍历字符的位置位于 visitedPos 之前
if (i < visitedPos)
RL[i] = min(RL[2 * midPos - i], visitedPos - i + 1);
// 当前遍历字符的位置与 visitedPos 重合
else
RL[i] = 1;
// 中心拓展(注意处理边界)
while (i - RL[i] >= 0 && i + RL[i] < slen && s_[i - RL[i]] == s_[i + RL[i]])
RL[i] += 1;
// 更新 visitedPos 和 midPos
if (i + RL[i] - 1 > visitedPos)
{
visitedPos = RL[i];
midPos = i;
}
// 统计回文子串数量
count += RL[i] / 2;
}
return count;
}
复杂度分析
时间复杂度: O ( n ) O(n) O(n)。
空间复杂度: O ( n ) O(n) O(n)。