文章目录
上一节中,我们介绍了 线性回归的原理,那么这篇文章就来用一个实际的例子来看一下如何用代码实现线性回归。
1 数据预处理
我们事先准备好了数据,保存在csv文件中,大致的数据结构如下,文件中有701行数据。
首先导入我们本节需要使用的库:
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.axes as ax
from matplotlib.animation import FuncAnimation
接下来读取文件、预处理,然后分割一下训练集和测试集。
(1)读取文件并删除空行
pd.read_csv用来读取csv文件,data.dropna() 删除 DataFrame 中包含缺失值的行。此操作会移除任何含有 NaN 或空值的记录。
csv_dir = '/content/drive/MyDrive/learning/data_for_lr.csv'
data = pd.read_csv(csv_dir)
# Drop the missing values
data = data.dropna()
(2)分割训练集和测试集
# training dataset and labels
train_input = np.array(data.x[0:500]).reshape(500, 1)
train_output = np.array(data.y[0:500]).reshape(500, 1)
# valid dataset and labels
test_input = np.array(data.x[500:700]).reshape(199, 1)
test_output = np.array(data.y[500:700]).reshape(199, 1)
data.x和data.y:使用pd.read_csv(csv_dir)读取 CSV 文件后,Pandas 会将 CSV 文件的每一列名称作为 DataFrame 中的列名,对应csv中的两列的列名x和y- 为什么要转化为numpy格式?
data是一个Pandas DataFrame对象,机器学习模型通常要求输入数据为 NumPy 数组,因为它提供高效的矩阵运算和更广泛的数学操作支持。此外,NumPy 与主流机器学习框架(如 Scikit-learn、TensorFlow)更兼容,性能优于 Pandas 数据结构。
- 以训练集为例:
data.x[0:500]表示取数据集中第 0 到 499 行的x列(假设 DataFrame 中有名为x的列)。reshape(500, 1)将一维数组调整为形状为 500 × 1 500 \times 1 500×1 的二维数组,便于与机器学习模型输入格式匹配。- 机器学习模型的输入通常是二维数组,形状为 ( n samples , n features ) (n_{\text{samples}}, n_{\text{features}}) (nsamples,nfeatures),表示 n samples n_{\text{samples}} nsamples 个样本,每个样本有 n features n_{\text{features}} nfeatures 个特征。
- 这里的输入特征只有一个x,输出特征只有一个y,所以两个数组都reshape成 500 × 1 500 \times 1 500×1
2 构建线性回归模型并绘制回归线
步骤:
- 在前向传播中,应用线性回归函数 Y = m x + c Y = mx + c Y=mx+c,其中参数 m m m 和 c c c 初始赋值为随机值。
- 然后编写一个函数用于计算损失函数,即均值。
现在我们打算实现一个LinearRegression类,即一个简单的线性回归模型,通过梯度下降进行参数优化,包括前向传播、代价函数计算、后向传播以及参数更新等关键步骤。
初始化方法
def __init__(self):
self.parameters = {}
- 初始化参数字典
self.parameters,即声明并初始化一个空字典,用于存储回归系数 m m m 和截距 c c c。
前向传播:forward_propagation
前向传播是机器学习模型从输入数据经过模型参数(如权重和偏置)计算输出预测值的过程,例如线性回归中通过公式 y = m x + c y = mx + c y=mx+c 计算结果。它用于生成预测值,并为损失函数计算提供基础。
def forward_propagation(self, train_input):
m = self.parameters['m']
c = self.parameters['c']
predictions = np.multiply(m, train_input) + c
return predictions
- 通过公式 y = m x + c y = mx + c y=mx+c 计算预测值,训练输入为 t r a i n _ i n p u t train\_input train_input,输出为预测值 p r e d i c t i o n s predictions predictions。
代价函数:cost_function
def cost_function(self, predictions, train_output):
cost = np.mean((train_output - predictions) ** 2)
return cost
- 使用均方误差(MSE)计算损失:
C
o
s
t
=
1
n
∑
(
y
a
c
t
u
a
l
−
y
p
r
e
d
i
c
t
e
d
)
2
Cost = \frac{1}{n} \sum (y_{actual} - y_{predicted})^2
Cost=n1∑(yactual−ypredicted)2。
np.mean用于计算数组元素的平均值
- 输入:预测值 p r e d i c t i o n s predictions predictions 和训练输出 t r a i n _ o u t p u t train\_output train_output。
- 输出:损失值 c o s t cost cost。
反向传播:backward_propagation
def backward_propagation(self, train_input, train_output, predictions):
derivatives = {}
df = (predictions - train_output)
dm = 2 * np.mean(np.multiply(train_input, df))
dc = 2 * np.mean(df)
derivatives['dm'] = dm
derivatives['dc'] = dc
return derivatives
- 计算梯度,在上一篇文章中我们计算了下面两个公式:
- 对 m m m 的梯度: ∂ C o s t ∂ m = 2 n ∑ ( y p r e d i c t e d − y a c t u a l ) ⋅ x i n p u t \frac{\partial Cost}{\partial m} = \frac{2}{n} \sum (y_{predicted} - y_{actual}) \cdot x_{input} ∂m∂Cost=n2∑(ypredicted−yactual)⋅xinput。
- 对 c c c 的梯度: ∂ C o s t ∂ c = 2 n ∑ ( y p r e d i c t e d − y a c t u a l ) \frac{\partial Cost}{\partial c} = \frac{2}{n} \sum (y_{predicted} - y_{actual}) ∂c∂Cost=n2∑(ypredicted−yactual)。
- 输入:训练输入 t r a i n _ i n p u t train\_input train_input,训练输出 t r a i n _ o u t p u t train\_output train_output,预测值 p r e d i c t i o n s predictions predictions。
- 输出:包含梯度 d m dm dm 和 d c dc dc 的字典。
参数更新:update_parameters
def update_parameters(self, derivatives, learning_rate):
self.parameters['m'] = self.parameters['m'] - learning_rate * derivatives['dm']
self.parameters['c'] = self.parameters['c'] - learning_rate * derivatives['dc']
- 使用梯度下降法更新参数,在上一篇文章中我们提到要使用下面的公式来更新参数:
- m = m − α ⋅ ∂ C o s t ∂ m m = m - \alpha \cdot \frac{\partial Cost}{\partial m} m=m−α⋅∂m∂Cost。
- c = c − α ⋅ ∂ C o s t ∂ c c = c - \alpha \cdot \frac{\partial Cost}{\partial c} c=c−α⋅∂c∂Cost。
- 输入:梯度字典 d e r i v a t i v e s derivatives derivatives 和学习率 l e a r n i n g _ r a t e learning\_rate learning_rate。
训练方法:train
完整代码如下:
def train(self, train_input, train_output, learning_rate, iters):
# Initialize random parameters
self.parameters['m'] = np.random.uniform(0, 1) * -1
self.parameters['c'] = np.random.uniform(0, 1) * -1
# Initialize loss
self.loss = []
# Initialize figure and axis for animation
fig, ax = plt.subplots()
x_vals = np.linspace(min(train_input), max(train_input), 100)
line, = ax.plot(x_vals, self.parameters['m'] * x_vals +
self.parameters['c'], color='red', label='Regression Line')
ax.scatter(train_input, train_output, marker='o',
color='green', label='Training Data')
# Set y-axis limits to exclude negative values
ax.set_ylim(0, max(train_output) + 1)
def update(frame):
# Forward propagation
predictions = self.forward_propagation(train_input)
# Cost function
cost = self.cost_function(predictions, train_output)
# Back propagation
derivatives = self.backward_propagation(
train_input, train_output, predictions)
# Update parameters
self.update_parameters(derivatives, learning_rate)
# Update the regression line
line.set_ydata(self.parameters['m']
* x_vals + self.parameters['c'])
# Append loss and print
self.loss.append(cost)
print("Iteration = {}, Loss = {}".format(frame + 1, cost))
return line,
# Create animation
ani = FuncAnimation(fig, update, frames=iters, interval=200, blit=True)
# Save the animation as a video file (e.g., MP4)
ani.save('linear_regression_A.gif', writer='ffmpeg')
plt.xlabel('Input')
plt.ylabel('Output')
plt.title('Linear Regression')
plt.legend()
plt.show()
return self.parameters, self.loss
这个训练的函数代码比较长,我们分三部分来讲解:
(1)初始化随机参数和绘制动画的初始设置
# Initialize random parameters
self.parameters['m'] = np.random.uniform(0, 1) * -1
self.parameters['c'] = np.random.uniform(0, 1) * -1
# Initialize loss
self.loss = []
# Initialize figure and axis for animation
fig, ax = plt.subplots()
x_vals = np.linspace(min(train_input), max(train_input), 100)
line, = ax.plot(x_vals, self.parameters['m'] * x_vals +
self.parameters['c'], color='red', label='Regression Line')
ax.scatter(train_input, train_output, marker='o',
color='green', label='Training Data')
# Set y-axis limits to exclude negative values
ax.set_ylim(0, max(train_output) + 1)
-
初始化随机参数: m m m 和 c c c 分别是线性回归模型的斜率和截距,使用随机负值初始化
-
初始化损失列表:
self.loss = [],用于记录每次迭代的损失值。 -
创建动画图像的坐标轴:
- 使用
plt.subplots()初始化图形。 - 使用
np.linspace在训练数据范围内生成100个等间距的 x x x 值。 - 用回归线
line和散点图scatter绘制初始数据分布和回归线。- 这两个函数不做深入解释了,主要是用动画显示一下结果
- 使用
-
设置 y y y 轴范围:
ax.set_ylim(0, max(train_output) + 1),避免负值干扰图形。
(2)定义动画更新逻辑
def update(frame):
# Forward propagation
predictions = self.forward_propagation(train_input)
# Cost function
cost = self.cost_function(predictions, train_output)
# Back propagation
derivatives = self.backward_propagation(
train_input, train_output, predictions)
# Update parameters
self.update_parameters(derivatives, learning_rate)
# Update the regression line
line.set_ydata(self.parameters['m']
* x_vals + self.parameters['c'])
# Append loss and print
self.loss.append(cost)
print("Iteration = {}, Loss = {}".format(frame + 1, cost))
return line,
-
前向传播:调用
self.forward_propagation(train_input)计算预测值 -
计算损失:调用
self.cost_function(predictions, train_output),基于均方误差(MSE)计算损失 -
反向传播:调用
self.backward_propagation计算梯度 -
参数更新:使用学习率 α \alpha α 和反向传播计算出来的梯度更新参数
-
更新回归线:根据新的 m m m 和 c c c 重新绘制回归线。
-
记录损失并打印:将当前迭代的损失追加到
self.loss中,并打印当前迭代信息。
(2)创建动画、保存和显示图像
# Create animation
ani = FuncAnimation(fig, update, frames=iters, interval=200, blit=True)
# Save the animation as a video file (e.g., MP4)
ani.save('linear_regression_A.gif', writer='ffmpeg')
plt.xlabel('Input')
plt.ylabel('Output')
plt.title('Linear Regression')
plt.legend()
plt.show()
return self.parameters, self.loss
-
创建动画:调用
FuncAnimation动态展示每次迭代后模型的变化,update函数在FuncAnimation中由frames=iters控制,总共被调用iters次,每帧调用一次,间隔由interval=200毫秒决定。 -
保存动画:将训练过程保存为 GIF 文件,便于分析。
-
显示图像:绘制最终的回归线和训练数据分布。
-
返回结果:最终返回优化后的参数和记录的损失值。
代码运行结果
#Example usage
linear_reg = LinearRegression()
parameters, loss = linear_reg.train(train_input, train_output, 0.0001, 20)
输出:
Iteration = 1, Loss = 4380.455128289033
Iteration = 1, Loss = 534.7906518669206
Iteration = 1, Loss = 71.34622937840669
Iteration = 1, Loss = 15.49613095399081
Iteration = 2, Loss = 8.765584291635278
Iteration = 3, Loss = 7.9544781683945
Iteration = 4, Loss = 7.856729049602253
Iteration = 5, Loss = 7.844947213272631
Iteration = 6, Loss = 7.843525370234688
Iteration = 7, Loss = 7.843352019334563
Iteration = 8, Loss = 7.8433291255257975
Iteration = 9, Loss = 7.843324363635718
Iteration = 10, Loss = 7.843321787040954
Iteration = 11, Loss = 7.843319473999822
Iteration = 12, Loss = 7.843317192921515
Iteration = 13, Loss = 7.843314915896804
Iteration = 14, Loss = 7.843312639562301
Iteration = 15, Loss = 7.843310363512657
Iteration = 16, Loss = 7.843308087699013
Iteration = 17, Loss = 7.843305812115446
Iteration = 18, Loss = 7.8433035367612325
Iteration = 19, Loss = 7.843301261636267
Iteration = 20, Loss = 7.843298986740505
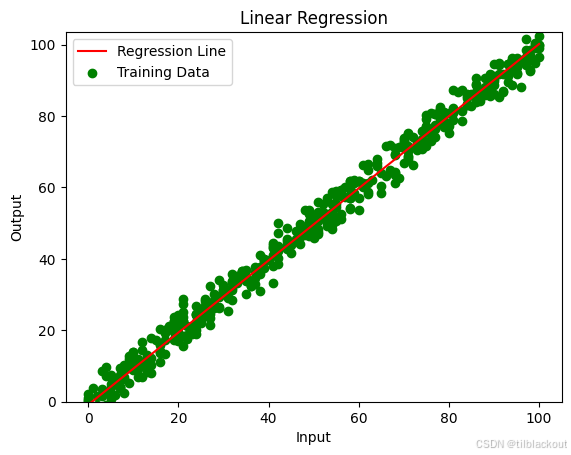
结果图如下,红色曲线为我们最终的回归曲线:
- 在本地自己运行上述代码,可以看到曲线红色曲线随着梯度下降更新参数的过程。
线性回归线提供了两个变量之间关系的最佳拟合线,捕获因变量 Y Y Y 随自变量 X X X 变化的总体趋势。
3 使用Pytorch实现线性回归
现在已经有许多优秀的机器学习库,如TensorFlow、Scikit-learn等,它们都能帮助我们快速实现线性回归等模型。本文选择PyTorch作为例子,展示如何更简洁地完成建模与训练,同时体验其灵活性与强大的自动微分功能。下面还是基于刚刚编写的代码,我们来看一下做得一些改动:
(1)库引入
import torch
from torch import nn
-
torch是 PyTorch 的核心库,提供了张量操作和基本数学计算功能,类似于 NumPy 的作用,但支持自动求导和 GPU 加速。 -
torch.nn是 PyTorch 中构建神经网络的核心模块,提供了实现深度学习模型所需的基本构件。
(2)数据处理
数据要转化为PyTorch的张量形式:
train_input = torch.tensor(data.x[0:500].values, dtype=torch.float32).view(-1, 1)
train_output = torch.tensor(data.y[0:500].values, dtype=torch.float32).view(-1, 1)
test_input = torch.tensor(data.x[500:700].values, dtype=torch.float32).view(-1, 1)
test_output = torch.tensor(data.y[500:700].values, dtype=torch.float32).view(-1, 1)
view(-1, 1):-1表示根据剩余维度自动计算大小,1表示将数据重新组织为一列(每个特征在单独的一列中)。
(3)线性回归类
class LinearRegression(nn.Module):
def __init__(self):
# 调用 nn.Module 的 __init__ 方法,初始化父类的属性和功能
super(LinearRegression, self).__init__()
# 定义线性层,输入为1,输出为1
self.linear = nn.Linear(1, 1)
# 前向传播,等价于前面我们写的forward_propagation
def forward(self, x):
return self.linear(x)
def train_model(self, train_input, train_output, learning_rate, iters):
# 定义损失函数
criterion = nn.MSELoss()
# 定义优化器
optimizer = torch.optim.SGD(self.parameters(), lr=learning_rate)
# 初始化损失列表
self.loss = []
# 初始化图像和动画
fig, ax = plt.subplots()
x_vals = torch.linspace(train_input.min(), train_input.max(), 100).view(-1, 1)
line, = ax.plot(x_vals.numpy(), self.forward(x_vals).detach().numpy(),
color='red', label='Regression Line')
ax.scatter(train_input.numpy(), train_output.numpy(), marker='o',
color='green', label='Training Data')
ax.set_ylim(0, train_output.max().item() + 1)
def update(frame):
# 前向传播
predictions = self.forward(train_input)
# 计算损失
loss = criterion(predictions, train_output)
# 反向传播
optimizer.zero_grad()
loss.backward()
# 更新参数
optimizer.step()
# 更新回归线
line.set_ydata(self.forward(x_vals).detach().numpy())
# 记录损失
self.loss.append(loss.item())
print(f"Iteration = {frame + 1}, Loss = {loss.item()}")
return line,
# 创建动画
ani = FuncAnimation(fig, update, frames=iters, interval=200, blit=True)
# 保存动画
ani.save('linear_regression_pytorch.gif', writer='ffmpeg')
# 显示图像
plt.xlabel('Input')
plt.ylabel('Output')
plt.title('Linear Regression')
plt.legend()
plt.show()
return self.linear.weight.data, self.linear.bias.data, self.loss
nn.Module是 PyTorch 中所有神经网络模型的基类。它为神经网络模型的构建和使用提供了一套通用框架。这里让LinearRegression类继承这个父类nn.Linear(1, 1):定义一个输入维度为1,输出维度为1的线性层- 参数存储在
self.linear.weight和self.linear.bias中,可以通过model.parameters()访问
- 参数存储在
| 改动 | 自己实现 | Pytorch |
|---|---|---|
| 前向传播 | def forward_propagation(self, train_input): m = self.parameters[‘m’] c = self.parameters[‘c’] predictions = np.multiply(m, train_input) + c return predictions | def forward(self, x): return self.linear(x) |
| 损失函数 | def cost_function(self, predictions, train_output): cost = np.mean((train_output - predictions) ** 2) return cost | criterion = nn.MSELoss() |
| 反向传播 | def update_parameters(self, derivatives, learning_rate): self.parameters[‘m’] = self.parameters[‘m’] - learning_rate * derivatives[‘dm’] self.parameters[‘c’] = self.parameters[‘c’] - learning_rate * derivatives[‘dc’] | optimizer = torch.optim.SGD(self.parameters(), lr=learning_rate) |
| PyTorch张量 vs Numpy | x_vals = torch.linspace(train_input.min(), train_input.max(), 100).view(-1, 1) line, = ax.plot(x_vals.numpy(), self.forward(x_vals).detach().numpy(), color=‘red’, label=‘Regression Line’) ax.scatter(train_input.numpy(), train_output.numpy(), marker=‘o’, color=‘green’, label=‘Training Data’) ax.set_ylim(0, train_output.max().item() + 1) | x_vals = np.linspace(min(train_input), max(train_input), 100) line, = ax.plot(x_vals, self.parameters[‘m’] * x_vals + self.parameters[‘c’], color=‘red’, label=‘Regression Line’) ax.scatter(train_input, train_output, marker=‘o’, color=‘green’, label=‘Training Data’) # Set y-axis limits to exclude negative values ax.set_ylim(0, max(train_output) + 1) |
- 在PyTorch中,上面的
update中就是用库中定义的前向传播、损失函数和反向传播函数了,就不放在表格中对比了。
最后我们运行一下这段代码:
# 使用示例
linear_reg = LinearRegression()
parameters, bias, loss = linear_reg.train_model(train_input, train_output, 0.0001, 20)
效果是和我们自己实现的差不多的。
- 由于PyTorch包含整个神经网络的功能,所以这里遇到的PyTorch中预定义的不同的优化器和损失函数,在后续学完所有的机器学习方法后再一起介绍,现在仅了解一下就好。
4 扩展:正则化
4.1 正则化解释
在机器学习和回归模型中,正则化是一种通过在目标函数中添加惩罚项来提高模型泛化能力的技术。主要目的是解决以下两个常见问题:
-
过拟合 (Overfitting)
当模型过于复杂,参数过多时,模型可能会记住训练数据中的噪声,从而导致在新数据上的表现变差。- 过拟合的迹象包括训练集上误差很低,但测试集误差很高。
- 正则化通过惩罚大幅度的参数值,限制模型复杂度,从而减少过拟合的风险。
-
多重共线性 (Multicollinearity)
在回归模型中,如果自变量之间高度相关,可能会导致系数的不稳定性。- 正则化可以通过增加惩罚项,使得模型更加鲁棒,从而缓解多重共线性问题。
什么情况下需要正则化
- 数据量少但特征多时,模型容易过拟合。
- 训练误差和测试误差之间的差异很大时,可能存在过拟合问题。
- 存在多重共线性(自变量高度相关)的情况下,系数可能会变得不稳定,需要通过正则化来约束系数。
- 希望对模型进行特征选择时,正则化(如 L 1 L1 L1)可以自动选择重要特征,将无关特征的系数压缩为零。
正则化的主要方法
(1)Lasso 回归 (L1 正则化)
Lasso 回归通过在线性回归目标函数中添加惩罚项来防止过拟合。
应用 Lasso 回归后的目标函数为:
J
(
θ
)
=
1
2
m
∑
i
=
1
m
(
y
^
i
−
y
i
)
2
+
λ
∑
j
=
1
n
∣
θ
j
∣
J(\theta) = \frac{1}{2m} \sum_{i=1}^m (\hat{y}_i - y_i)^2 + \lambda \sum_{j=1}^n | \theta_j |
J(θ)=2m1i=1∑m(y^i−yi)2+λj=1∑n∣θj∣
- 第一项表示最小二乘误差 (预测值和实际值之间平方差)。
- 第二项是 L 1 L1 L1 正则化项,惩罚回归系数的绝对值之和。
- 优点:Lasso 可以将一些系数缩减为零,从而实现特征选择。
- 缺点:对于特征数大于样本数时,Lasso 的表现可能不稳定。
(2)Ridge 回归 (L2 正则化)
Ridge 回归通过向目标函数添加正则化项来防止过拟合,尤其适用于高多重共线性的数据集。
应用 Ridge 回归后的目标函数为:
J
(
θ
)
=
1
2
m
∑
i
=
1
m
(
y
^
i
−
y
i
)
2
+
λ
∑
j
=
1
n
θ
j
2
J(\theta) = \frac{1}{2m} \sum_{i=1}^m (\hat{y}_i - y_i)^2 + \lambda \sum_{j=1}^n \theta_j^2
J(θ)=2m1i=1∑m(y^i−yi)2+λj=1∑nθj2
- 第一项表示最小二乘误差。
- 第二项惩罚回归系数平方值之和。
- 优点:Ridge 能够很好地处理多重共线性问题,使模型更加稳定。
- 缺点:Ridge 不能将系数压缩到零,无法进行特征选择。
(3)Elastic Net 回归
Elastic Net 回归结合了
L
1
L1
L1 和
L
2
L2
L2 正则化的优点。
目标函数为:
J
(
θ
)
=
1
2
m
∑
i
=
1
m
(
y
^
i
−
y
i
)
2
+
α
λ
∑
j
=
1
n
∣
θ
j
∣
+
(
1
−
α
)
2
λ
∑
j
=
1
n
θ
j
2
J(\theta) = \frac{1}{2m} \sum_{i=1}^m (\hat{y}_i - y_i)^2 + \alpha \lambda \sum_{j=1}^n |\theta_j| + \frac{(1 - \alpha)}{2} \lambda \sum_{j=1}^n \theta_j^2
J(θ)=2m1i=1∑m(y^i−yi)2+αλj=1∑n∣θj∣+2(1−α)λj=1∑nθj2
- 第一项是最小二乘误差。
- 第二项是 L 1 L1 L1 正则化,第三项是 Ridge 回归。
- λ \lambda λ 控制整体正则化强度。
- α \alpha α 控制 L 1 L1 L1 和 L 2 L2 L2 正则化的混合比例。
- 优点:适用于高维数据和特征数量远大于样本数量的场景,综合了 Lasso 和 Ridge 的优势。
总结
正则化是解决机器学习中过拟合和多重共线性问题的重要方法。在模型复杂或数据稀疏的情况下,正则化不仅能提升模型的泛化能力,还能实现特征选择。根据具体需求,可以选择 Lasso、Ridge 或 Elastic Net。
4.2 正则化实例
我们以一个简单的数据集为例,模拟房价预测:
| 房屋面积 | 位置评分 | 噪音等级 | 装修评分 | 价格 |
|---|---|---|---|---|
| 1000 | 8 | 4 | 7 | 300,000 |
| 1200 | 9 | 5 | 6 | 350,000 |
| 850 | 7 | 3 | 8 | 280,000 |
| 1300 | 9 | 5 | 7 | 370,000 |
| 900 | 7 | 4 | 6 | 290,000 |
- 特征:房屋面积、位置评分、噪音等级、装修评分。
- 目标:价格。
正则化前后的对比
(1)正则化之前
- 使用普通的线性回归训练模型。
- 现象:
- 模型可能为每个特征赋予较大的权重。
- 噪音等级(对房价的影响较小)也可能被分配较大的系数,增加模型复杂度。
- 训练集的误差很小,但在测试集上表现差(过拟合)。
| 特征权重(未正则化) |
|---|
| 房屋面积:100 |
| 位置评分:50 |
| 噪音等级:30 |
| 装修评分:20 |
(2)正则化之后
- 使用 Lasso 正则化 来限制不重要特征的影响。
- 现象:
- 噪音等级的系数被压缩为 0(表示对价格预测影响很小)。
- 保留对价格有显著影响的特征,如房屋面积和位置评分。
- 模型更加简单,泛化能力更强,在测试集上表现更好。
| 特征权重(Lasso 正则化后) |
|---|
| 房屋面积:90 |
| 位置评分:40 |
| 噪音等级:0 |
| 装修评分:15 |
正则化总结
- 未正则化时:所有特征都会被赋予权重,容易导致模型复杂且过拟合。
- 正则化后:通过缩减或移除不重要的特征,提高模型的简洁性和泛化能力。
5 总结
线性回归广泛应用于金融、经济学、心理学等领域,以理解和预测变量行为。例如,在金融领域,线性回归可用于研究公司股票价格与收益之间的关系,或根据过去的表现预测未来的货币价值。 优点与缺点如下:
优点
- 简单易懂,易于实现,系数具有可解释性。
- 计算效率高,适合处理大数据集,非常适合实时应用。
- 与其他算法相比,对异常值较为鲁棒。
- 常作为更复杂模型的基线模型。
- 历史悠久,广泛应用于各种机器学习库。
缺点
- 假设因变量与自变量之间是线性关系,若该假设不成立,模型表现可能较差。
- 对多重共线性敏感,可能导致系数方差膨胀和预测不稳定。
- 需要对特征进行预处理,确保输入数据适合模型使用。
- 容易发生过拟合或欠拟合。过拟合时,模型学习训练数据过好,无法泛化到新数据;欠拟合时,模型过于简单,无法捕获数据的潜在关系。
- 对于复杂变量关系,解释能力有限。
结论
线性回归是一种基础的机器学习算法,因其简单性、可解释性和高效性而备受推崇。它对于理解变量关系和进行预测非常有用。然而,其线性假设和对多重共线性的敏感性在使用时需要注意。如果这些限制条件被充分考虑,线性回归可以成为数据分析和预测的强大工具。