上一节我们了解了有限域的定义,并使用代码进行实现。作为区块链技术的底层技术支柱之一,它跟有限域有着非常紧密的联系,正式因为如此,椭圆曲线才能用来给区块链创建公钥,由此形成区块链钱包的地址。
对椭圆曲线而言,我们并不关心它本身,但是我们关系椭圆曲线上的点,以及这些点在特定操作下所形成的性质。因此我们代码的逻辑在实现椭圆曲线上的点,首先我们实现代码如下:
```python
class EllipticPoint:
def __init__(self, x, y, a, b):
"""
a, b为椭圆曲线方程 y^2 = x ^ 3 + ax + b
对于区块链的椭圆曲线a取值为0,b取值为7,其专有名称为secp256k1
由此在初始化椭圆曲线点时,必须确保(x,y)位于给定曲线上
"""
if y**2 != x**3 + a*x + b:
raise ValueError(f'({x}, {y}) is not on the curve')
self.x = x
self.y = y
self.a = a
self.b = b
def __eq__(self, other):
"""
两个点要相等,我们不能只判断x,y是否一样,必须判断他们是否位于同一条椭圆曲线
"""
return self.x == other.x and self.y == other.y and self.a == other.a and self.b == other.b
def __ne__(self, other):
return self.x != other.x or self.y != other.y or self.a != other.a or self.b != other.b
我们创建几个实例然后验证一下上面的代码:
'''
设置曲线y^2 = x ^ 3 + 5x + 7, (a=5, b=7)
'''
b = EllipticPoint(-1, -1, 5, 7)
c = EllipticPoint(18, 77, 5, 7)
print(b == c)
print(b != c)
#下面的点不在曲线上因此会出现异常
d = EllipticPoint(5, 7, 5, 7)
在上面代码中我们创建了三个椭圆曲线点,前两个点在曲线上,第三个点不在曲线上,因此实例化点d时会产生异常,运行结果如下:
False
True
Traceback (most recent call last):
File "/Users/my/PycharmProjects/pythonProject3/blockchain_curve.py", line 104, in <module>
d = EllipticPoint(5, 7, 5, 7)
File "/Users/my/PycharmProjects/pythonProject3/blockchain_curve.py", line 78, in __init__
raise ValueError(f'({x}, {y}) is not on the curve')
ValueError: (5, 7) is not on the curve
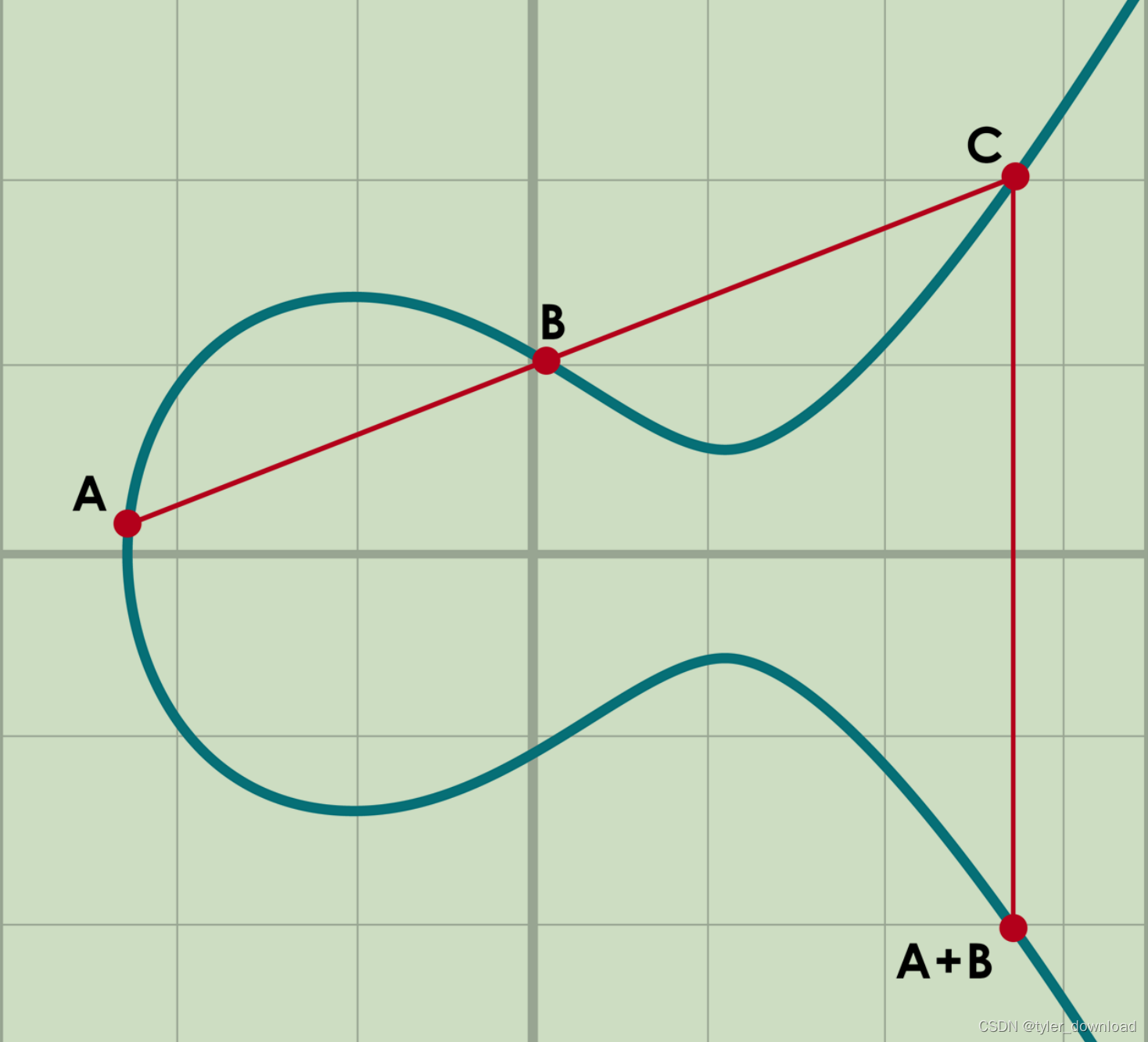
在上一节我们提到过椭圆曲线上的点的加法,选取曲线上两点,我们做他们的连线,此时会有三种情况,两点联系延长后跟曲线相交于第三点,如下图:
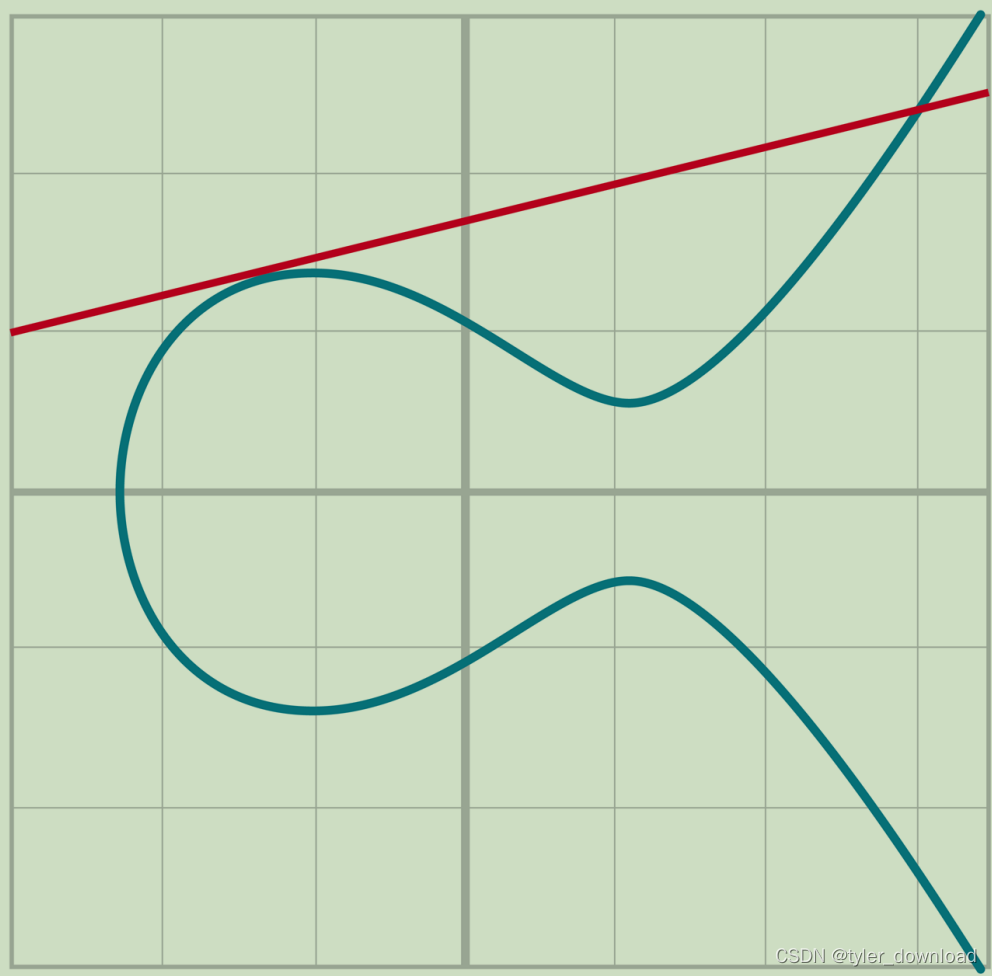
第二种情况如下,两点在同一条直线上,于是两点连线跟曲线不再有第三个交点:
还记得上一节我们提过有限域必然包含一个点"0",它跟集合内任何点a做"+“运算,结果是还是点a。上面情况就对应点"0”,虽然上面直线跟曲线没有第三个交点,但是我们可以“定义”这条直线跟曲线在“无限远”处相加,而那个交点就是"0",于是这种情况下直线跟曲线的两个交点互为“相反数”,如果我们把上面交点记作a,那么下面的那个交点就对应为-a, 当曲线上两个点的连线与y轴平行时,我们把这两个点的“+“运算结果记作"0”。
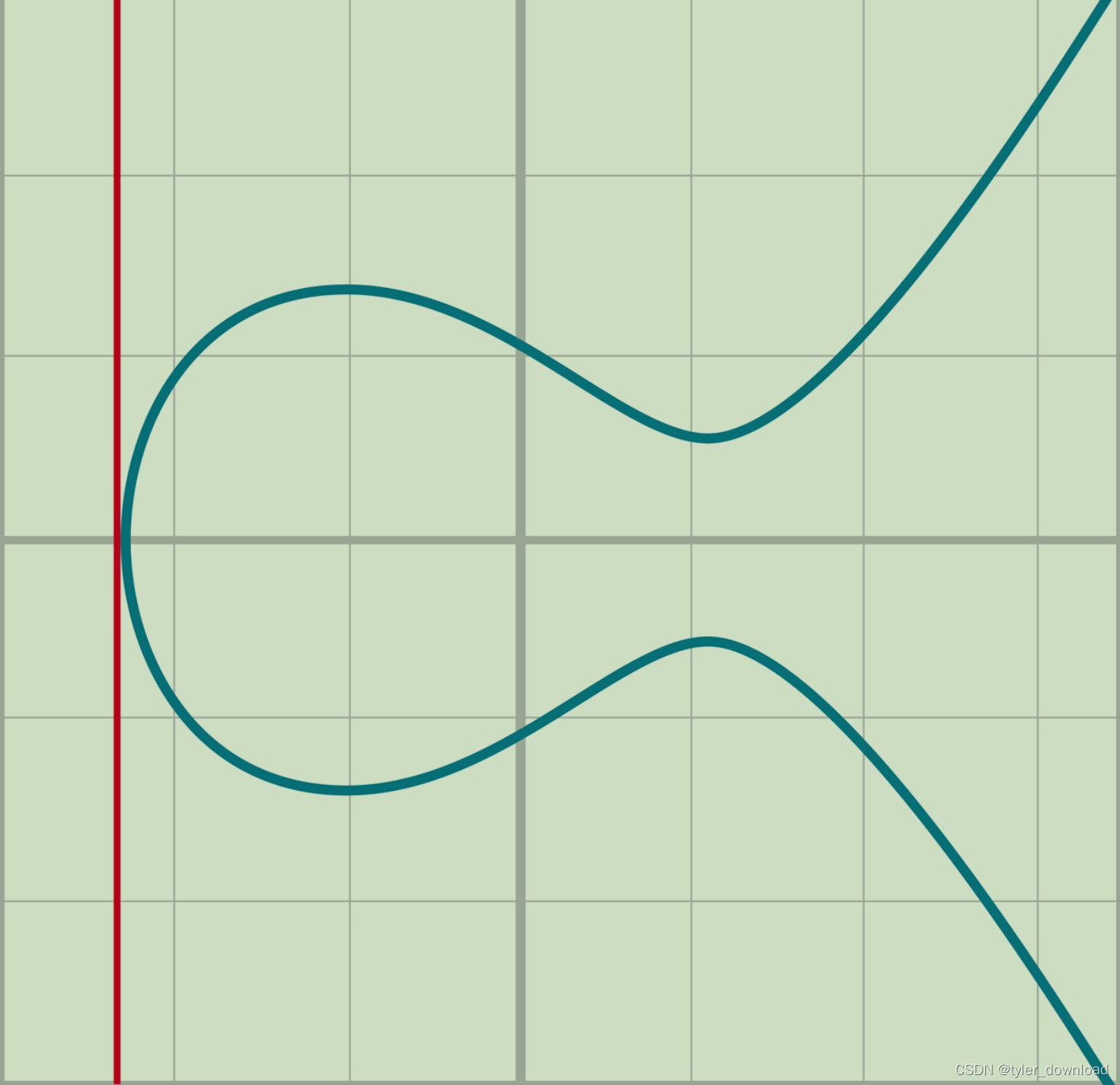
还有第三种情况是椭圆曲线上的两个点重合,也就是他们其实是同一个点,这样两点连线就会形成一条切线:
在椭圆曲线上选择任意两点,他们执行"+"操作后,第三点在哪里从数学上是无法预料的,这就形成了椭圆曲线能加密的基础。下面我们实现点的”+“操作,首先我们针对第二种情况,由于两点在同一直线上时,第三点跟曲线”相加“于无限远处,这个”交点“我们使用x=None,y=None,来表示,同时确保这样的点与其他任何点a做”+“操作,结果都是a,我们看看代码实现:
class EllipticPoint:
def __init__(self, x, y, a, b):
self.x = x
self.y = y
self.a = a
self.b = b
"""
x == None, y == None对应点"0"
"""
if x is None or y is None:
return
"""
a, b为椭圆曲线方程 y^2 = x ^ 3 + ax + b
对于区块链的椭圆曲线a取值为0,b取值为7,其专有名称为secp256k1
由此在初始化椭圆曲线点时,必须确保(x,y)位于给定曲线上
"""
if y ** 2 != x ** 3 + a * x + b:
raise ValueError(f'({x}, {y}) is not on the curve')
def __eq__(self, other):
"""
两个点要相等,我们不能只判断x,y是否一样,必须判断他们是否位于同一条椭圆曲线
"""
return self.x == other.x and self.y == other.y and self.a == other.a and self.b == other.b
def __ne__(self, other):
return self.x != other.x or self.y != other.y or self.a != other.a or self.b != other.b
def __add__(self, other):
"""
实现"+"操作,首先确保两个点位于同一条曲线,也就是他们对应的a,b要相同
"""
if self.a != other.a or self.b != other.b:
raise TypeError(f"points {self}, {other} not on the same curve")
#如果其中有一个是"0"那么"+"的结果就等于另一个点
if self.x is None:
return other
if other.x is None:
return self
def __repr__(self):
return f"EllipticPoint(x:{self.x},y:{self.y},a:{self.a}, b:{self.b})"
上面代码修改了原来初始化函数的实现,如果x,y两个分量有一个是None,那么它就对应”0“点,在实现”+“操作对应的__add__函数,如果相加的两个点中有一个是"0",那么结果就等于另一个点,我们测试上面实现看看结果:
zero + p1 is EllipticPoint(x:-1,y:-1,a:5, b:7)
zero + p2 is EllipticPoint(x:-1,y:1,a:5, b:7)
输出结果符合我们的预期。下面我们实现三种”+“情况中最简单的一种,那就是两点在同一直线上,也就是点的x分量相同,但y分量互为相反数,同时这样的两个点进行”+“操作后,所得结果就是”0“,我们看看实现:
def __add__(self, other):
"""
实现"+"操作,首先确保两个点位于同一条曲线,也就是他们对应的a,b要相同
"""
if self.a != other.a or self.b != other.b:
raise TypeError(f"points {self}, {other} not on the same curve")
#如果其中有一个是"0"那么"+"的结果就等于另一个点
if self.x is None:
return other
if other.x is None:
return self
"""
两点在同一直线上,也就是x相同,y互为相反数
"""
if self.x == other.x and self.y == -other.y:
return __class__(None, None, self.a, self.b)
我们测试一下上面代码:
p1 = EllipticPoint(-1, -1, 5, 7)
p2 = EllipticPoint(-1, 1, 5, 7)
# print(f"zero + p1 is {zero + p1}")
# print(f"zero + p2 is {zero + p2}")
print(f"p1 + p2 = {p1 + p2}")
上面代码运行结果:
p1 + p2 = EllipticPoint(x:None,y:None,a:5, b:7)
它与我们预期一致,下面我们实现较为复杂的情况,也就是第三种,两点形成的直线与曲线相交于第3点,这里需要一些数学推导,给定两点(x1,y1),(x2,y2),首先我们获得这两点连接后所形成直线的斜率k,根据高中代数有k = (y2 - y1)/(x2 - x1),同时两点对应直线方程有y = k * (x - x1) + y1,由于这条直线与椭圆曲线相交的第三点同时位于直线和曲线上,因此第三点的坐标一定同时满足这两个方程:
y = k*(x - x1)+y1
y^2 = x^3 + a*x + b
把第一个方程的y代入到第二个方程有:
(k*(x - x1)+y1)^2 = x^3 + a*x + b
把上面公式的右边部分挪到左边同时进行展开就有:
x^3 - k^2 * x^2 +(a + 2*s^2*x1 - 2*k*y1)*x + b - k^2(x1)^2 + 2*k*(x1)*(y1) - (y1)^2 = 0 (1)
如果我们使用(x3, y3)表示第三点,那么(x1,y1),(x2,y2),(x3,y3)肯定能满足下面方程:
(x-x1)*(x-x2)*(x-x3) = 0
把上面式子展开有:
x^3 - (x1+x2+x3)*x^2 + (x1*x2 + x1*x3 + x2*x3)*x - (x1*x2*x3) = 0 (2)
如果我们把(1)和(2)中对应x ^ 3, x ^ 2, x ^ 1, 已经常数项对应起来:
k^2 -> (x1+x2+x3) (3)
(a + 2 * s^2*x1 - 2*k*y1) -> (x1*x2 + x1*x3 + x2*x3)
b - k^2(x1)^2 + 2*k*(x1)*(y1) - (y1)^2 -> (x1*x2*x3)
根据韦达定理
上面(3)中->可以换成=,于是我们可以解出x3:
x3 = k^2 - x2 - x1 (4)
然后把x3代入到直线方程解出y3:
y3 = k * (x3 - x1) + y1 (5)
#记得要根据x轴做对称得到"+"对应结果
y = -y3 = k*(x1-x3) - y1 (6)
由此我们可以根据公式(4),(6)直接找到相交的第三点,代码实现如下:
def __add__(self, other):
"""
实现"+"操作,首先确保两个点位于同一条曲线,也就是他们对应的a,b要相同
"""
if self.a != other.a or self.b != other.b:
raise TypeError(f"points {self}, {other} not on the same curve")
#如果其中有一个是"0"那么"+"的结果就等于另一个点
if self.x is None:
return other
if other.x is None:
return self
"""
两点在同一直线上,也就是x相同,y互为相反数
"""
if self.x == other.x and self.y == -other.y:
return __class__(None, None, self.a, self.b)
"""
计算两点连线后跟曲线相交的第3点,使用韦达定理
"""
x1 = self.x
y1 = self.y
x2 = other.x
y2 = other.y
k = (y2 - y1) / (x2 - x1)
x3 = k ** 2 - x1 - x2
y3 = k * (x1 - x3) - y1
if self != other:
return __class__(x3, y3, self.a, self.b)
我们测试一下上面实现:
#测试两点直线与曲线相交于第三点
p1 = EllipticPoint(2, 5, 5, 7)
p2 = EllipticPoint(-1, -1, 5, 7)
print(f"p1 + p2 = {p1 + p2}")
上面代码运行后结果为:
p1 + p2 = EllipticPoint(x:3.0,y:-7.0,a:5, b:7)
最后我们实现两点连线变成曲线切线的情况。由于两点相同,因此我们不能像前面那样直接计算直线的斜率,因为k = (y2 - y1)/(x2 - x1),此时x2 = x1,于是分母为0,因此这里我们要借助高等数学的微积分:曲线在某一点处切线的斜率等于曲线在该点处的微分,根据曲线方程:
y^2 = x ^ 3 + a*x + b
两边分别对x进行微分有
2y d(y/x) = 3 * x^2 + a
于是有
k = d(y/x) = (3x^2 +a) / 2y
有了斜率后,我们就能使用(4),(6)来完成第3点坐标的计算,由此前面代码修改如下:
def __add__(self, other):
"""
实现"+"操作,首先确保两个点位于同一条曲线,也就是他们对应的a,b要相同
"""
if self.a != other.a or self.b != other.b:
raise TypeError(f"points {self}, {other} not on the same curve")
# 如果其中有一个是"0"那么"+"的结果就等于另一个点
if self.x is None:
return other
if other.x is None:
return self
"""
两点在同一直线上,也就是x相同,y互为相反数
"""
if self.x == other.x and self.y == -other.y:
return __class__(None, None, self.a, self.b)
"""
计算两点连线后跟曲线相交的第3点,使用韦达定理
"""
x1 = self.x
y1 = self.y
x2 = other.x
y2 = other.y
if self == other:
# 如果两点相同,根据微分来获得切线的斜率
k = (3 * self.x ** 2 + self.a) / 2 * self.y
else:
k = (y2 - y1) / (x2 - x1)
x3 = k ** 2 - x1 - x2
y3 = k * (x1 - x3) - y1
return __class__(x3, y3, self.a, self.b)
我们测试一下上面代码效果:
#测试两点相同所形成切线与曲线的交点
p1 = EllipticPoint(-1, -1, 5, 7)
print(f"p1 + p1 = {p1 + p1}")
上面代码运行后所得结果如下:
p1 + p1 = EllipticPoint(x:18.0,y:77.0,a:5, b:7)
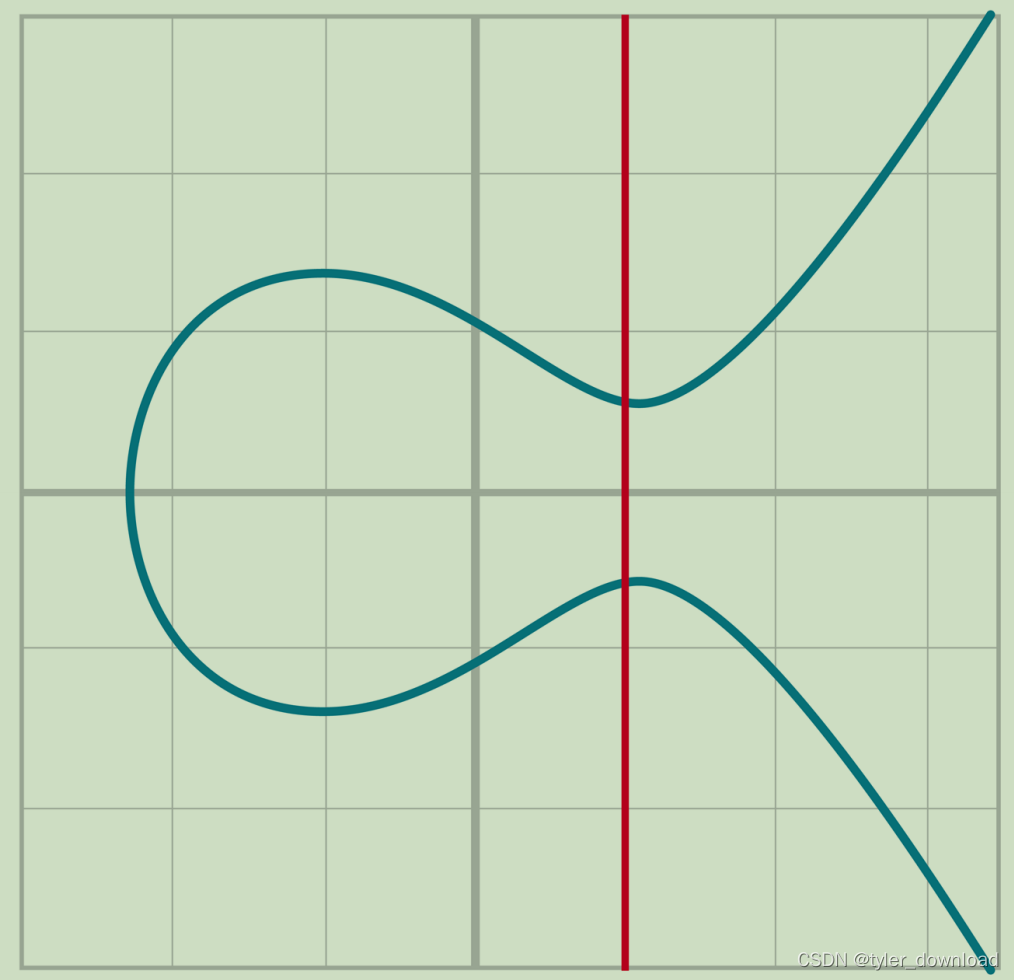
最后还有一种特殊情况如下:
这种情况对应点的y分量为0,这时我们不能使用微分来计算曲线斜率,因此我们在__add__中增加对这种情况的判断即可:
def __add__(self, other):
"""
特殊情况,两点相同而且y分量为0
"""
if self == other and self.y == 0:
return __class__(None, None, self.a, self.b )
#余下代码省略
....
以上就是椭圆曲线上点“+”操作的实现。在区块链应用中,首先需要选定曲线上一个特定点G,然后产生集合{1G, 2G, …},这个集合将能满足上一节我们描述的有限域属性,要创建区块链钱包地址,我们首先选择一个很大的数k,它也叫秘钥,然后计算k * G,所得结果就是公钥,我们把公钥再进行一系列哈希和编码后就能得到钱包地址,更多内容请在b站搜索coding迪斯尼。