Eigen

1.使用Map函数，c++数组与 eigen矩阵的转换

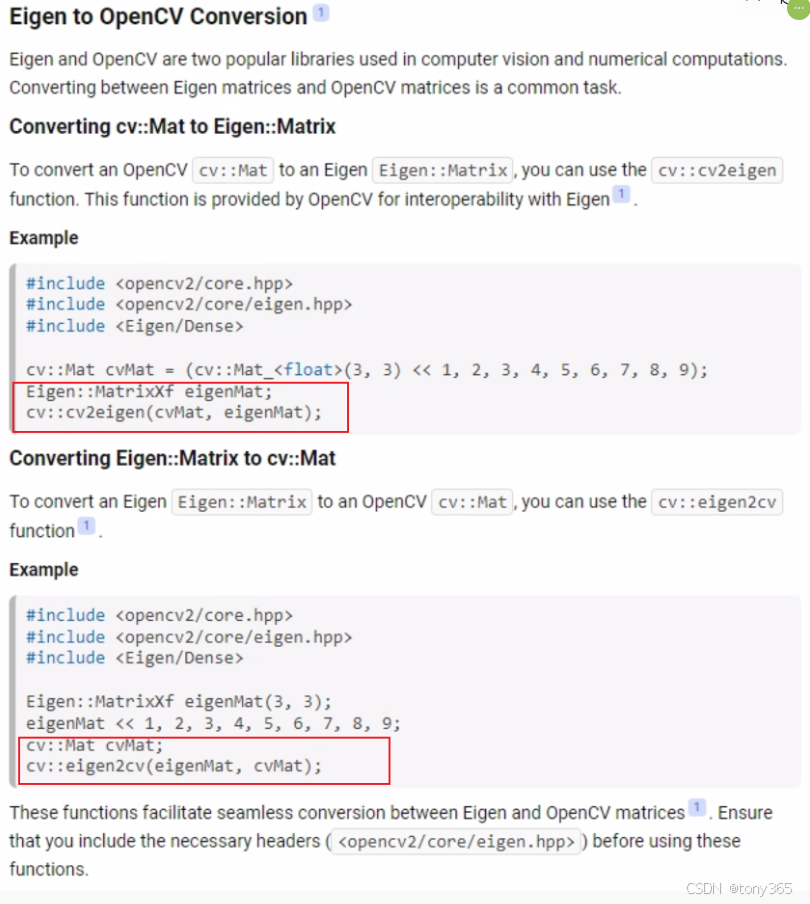
2.eigen矩阵与opencv互转

3.eigen使用总结

https://zxl19.github.io/eigen-note/
https://eigen.tuxfamily.org/dox/group__QuickRefPage.html

4.eigen visual studio 和 ubuntu上

a.ubuntu上只需要CMakeLists.txt中添加

include_directories(“/home/xx/software/eigen-3.4.0”)

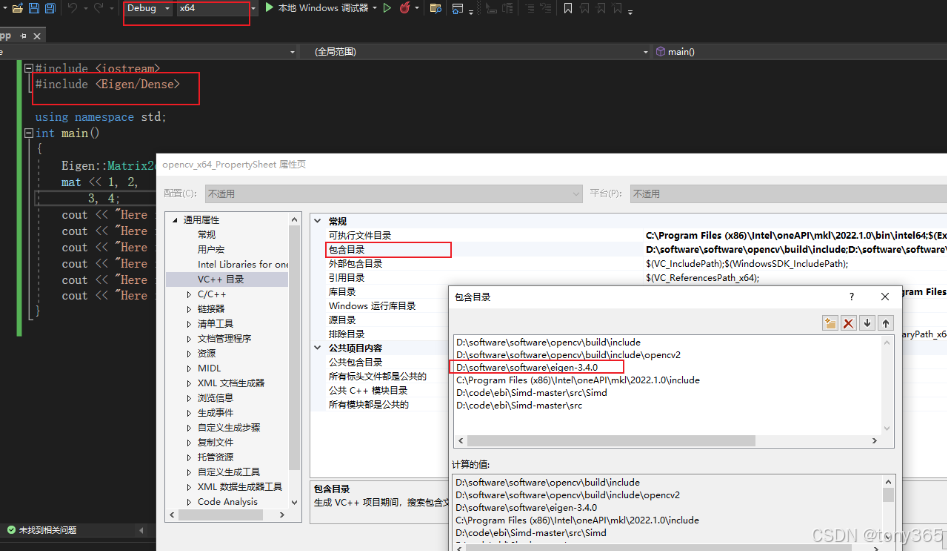
b.eigen 库在visual studio中的使用：
只需要添加包含目录即可

1）

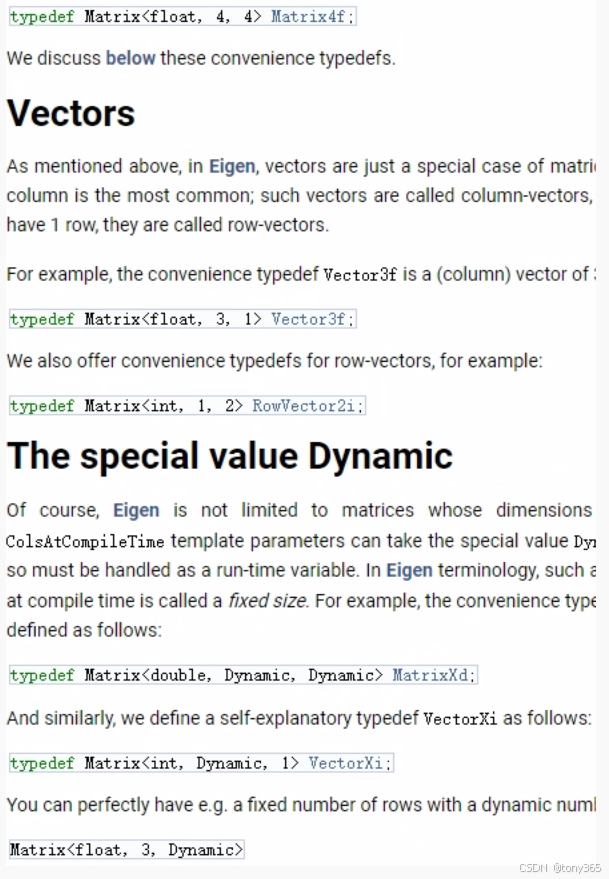
在eigen中， matrices 和 vectors都是 Matrix template class的对象。
Vectors 是matrices的特殊case：行数为1或者列数为1

模板类一共有六个参数，一般使用前三个参数就足够了。比如

2）

Dynamic关键字 指示动态矩阵动态向量。 动态是运行时才知道size大小。
静态时编译时就知道size大小。一般比较小的矩阵可以使用静态。
静态和动态类似于：

int a[16];
int *a = new int[1000*1000];

3）初始化的方法

4）元素获取

用括号
m(1,2) //第2行第3列

5）resize

m.rows() m.cols() m.size()
resize 只能操作固定size的矩阵，如果resize后数量不变则无操作，数量变化会删除原来的数据

6）赋值操作

a = b //相当于把b copy到 a, 如果ab大小不同，会有resize的操作。

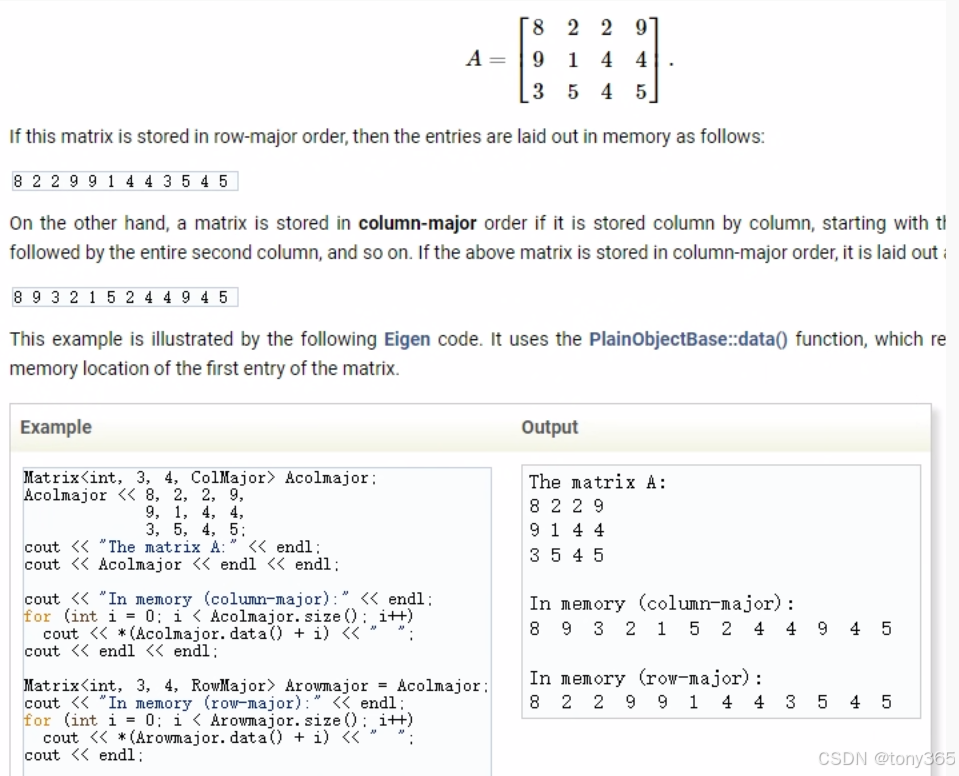
7）存储顺序

column major or row major

如果没有指定，默认是 ColMajor。
且两者可以互相转换，转换方法如下：

=======================================================================

8）算术操作

加减操作。必须类型（Scalar）相同，size相同。

矩阵与scalar的乘法，除法操作。

9）算术表达式

下面是可行的，而且可以更好的被优化

a = 3*b + 4*c - x/2;

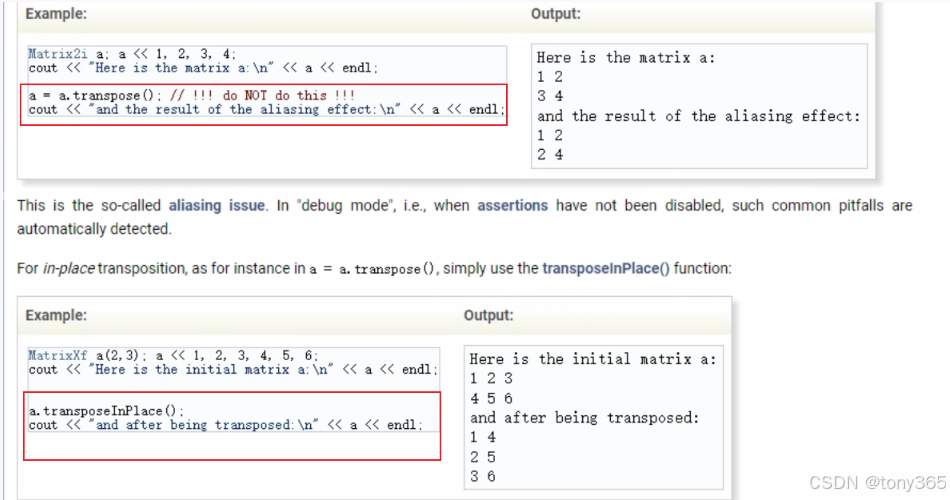
10） 转置

11） 矩阵相乘

c = a * b -> [m,n] @ [n,m] = [m, m]

12）内积

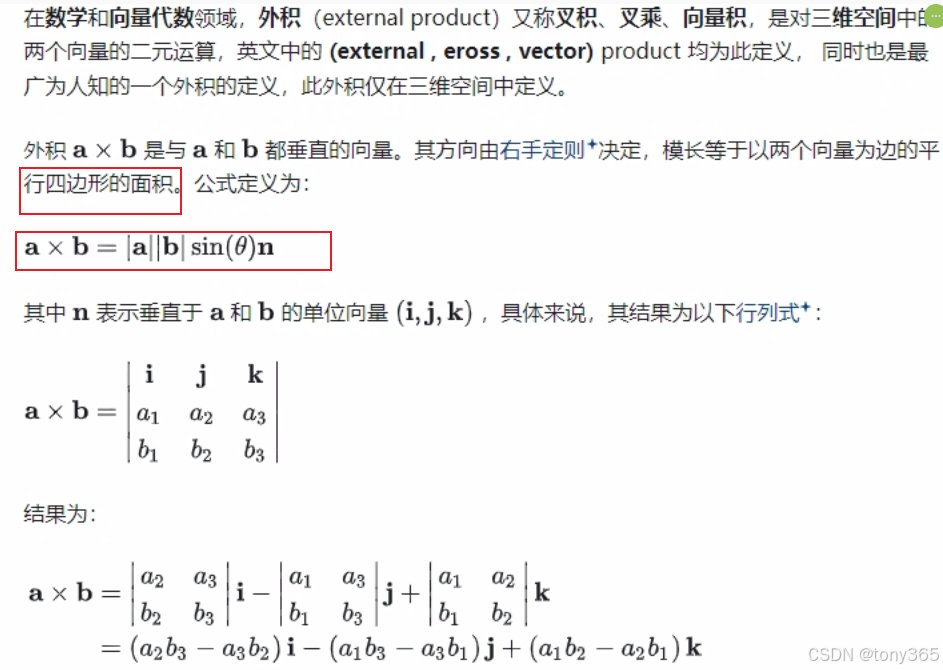
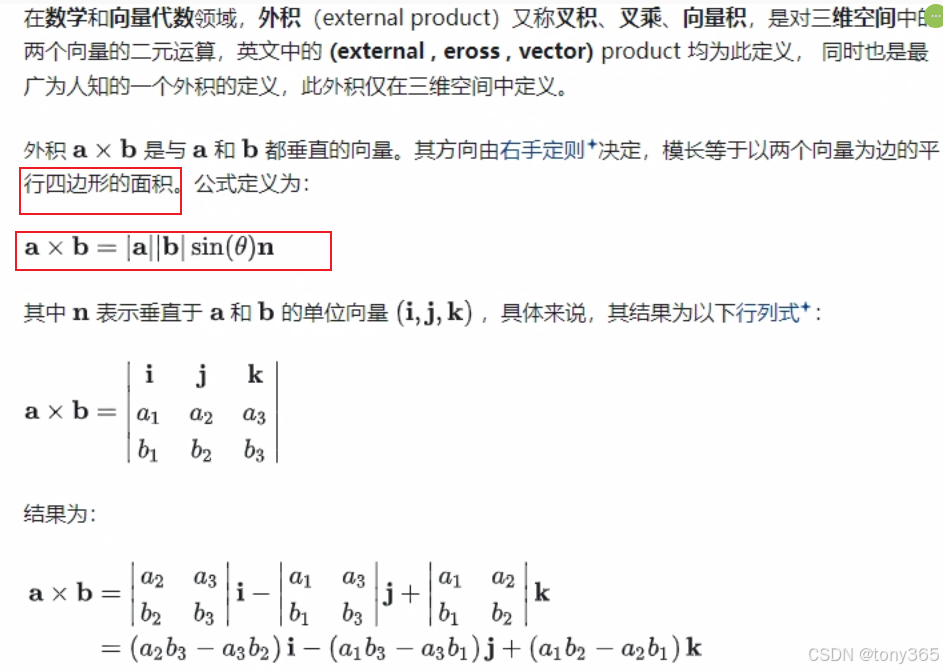
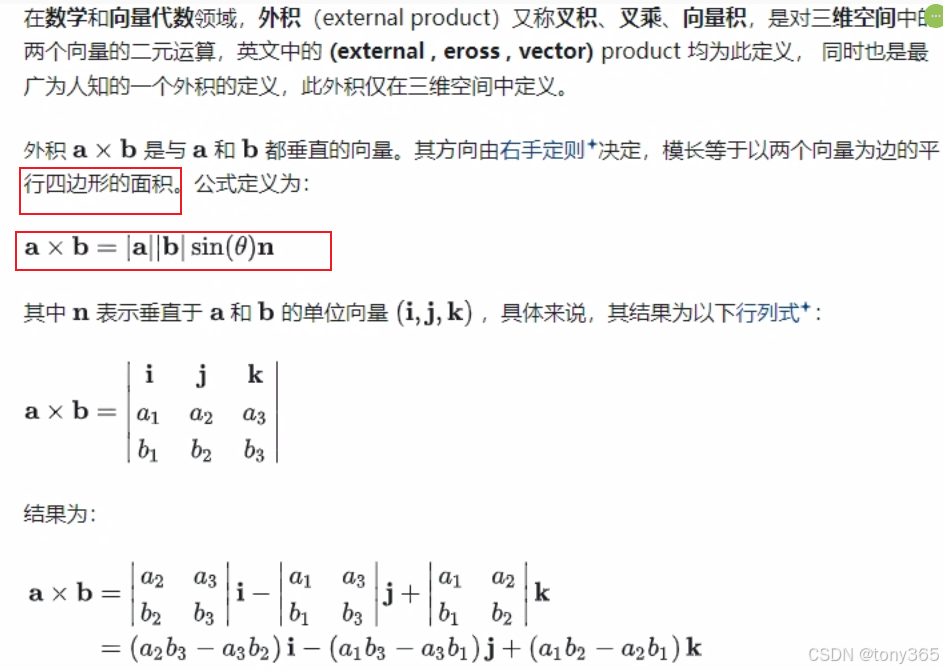
13）外积

14）eigen中内积和外积分别是 dot, cross

dot适用于任意长度的向量
cross只适用于长度为3的vector

15）reduction 操作

===============================================================================
array class

16）array

matrix目的是为了线性集合操作，比如矩阵相乘。
Array 可以更好的执行 element-wise 操作。
比如对矩阵+上一个数，或者两个矩阵对应元素相乘。

定义

对应元素 加，减，乘的操作略

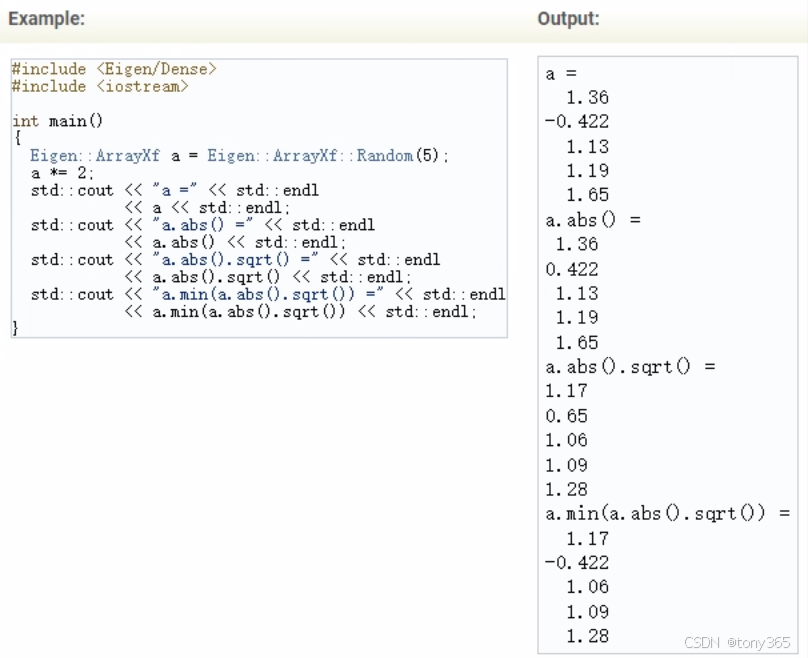
对应元素 abs, sqrt, min, max

17） array 和matrix

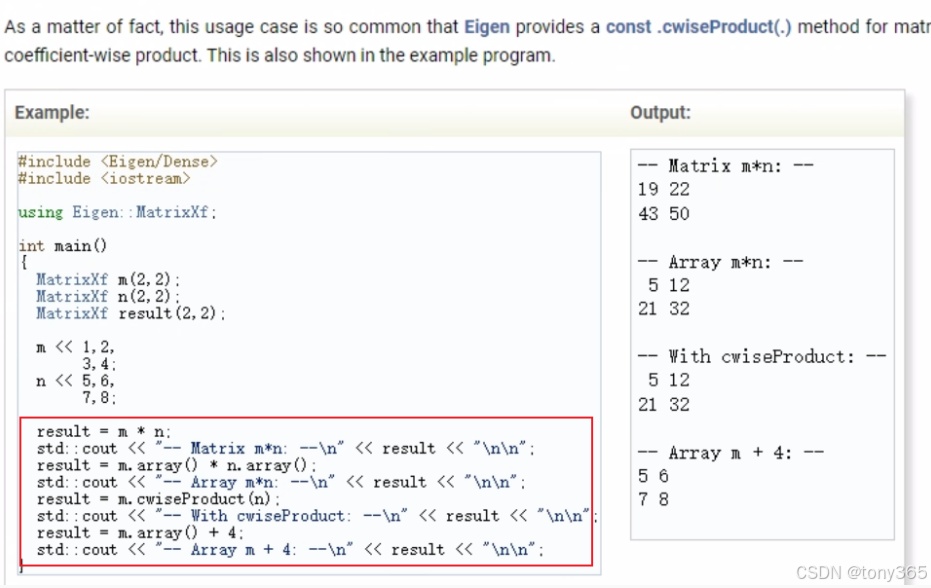
两个类的操作是不能互通的。因此如果你既想要矩阵相乘，又想要对应元素相乘，这个时候要首先进行转换。

.array() 和 .matrix() 可以是左值也可以是右值。而且基本上没有耗时

=======================================================================================

对于matrix

18）matrix : block(), row(), col() 和其他

block 输入 起始坐标（row,col）和对应高度宽度（height, width），输出矩形数据

m.row(i)
m.col(j)

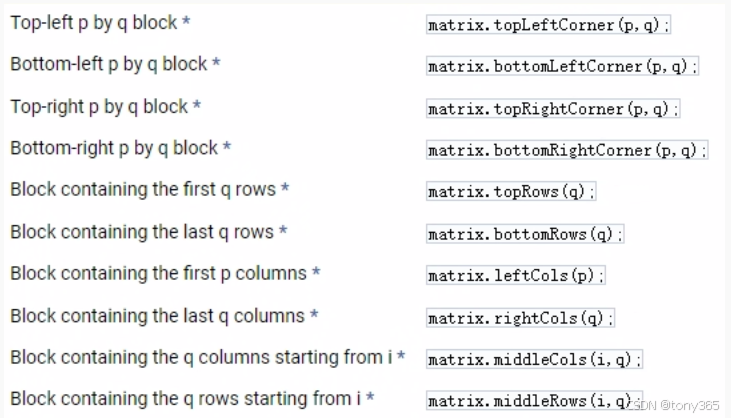
其他取矩阵的操作

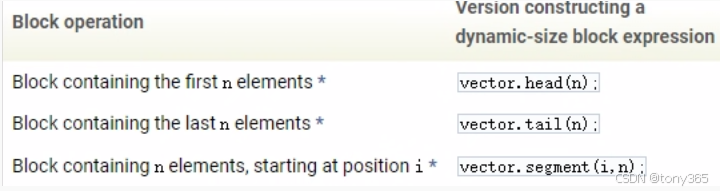
19）vector： head(), tail(), segment()

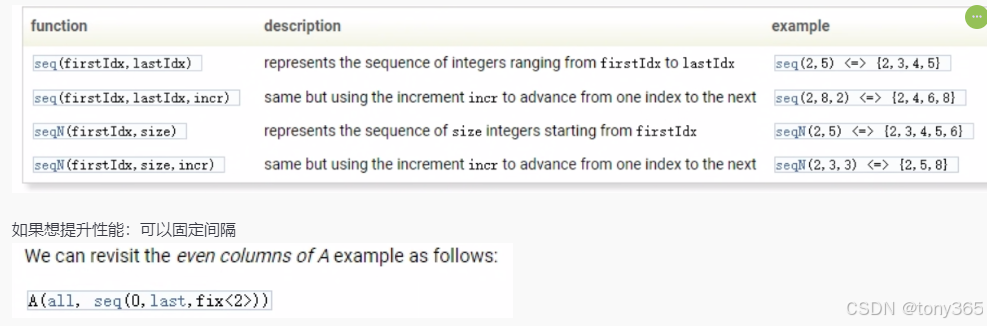
20）slicing和indexing 操作

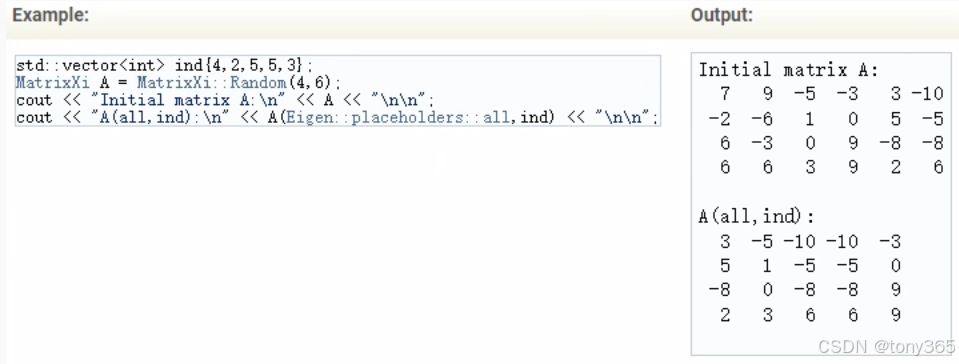
21）根据索引提取列

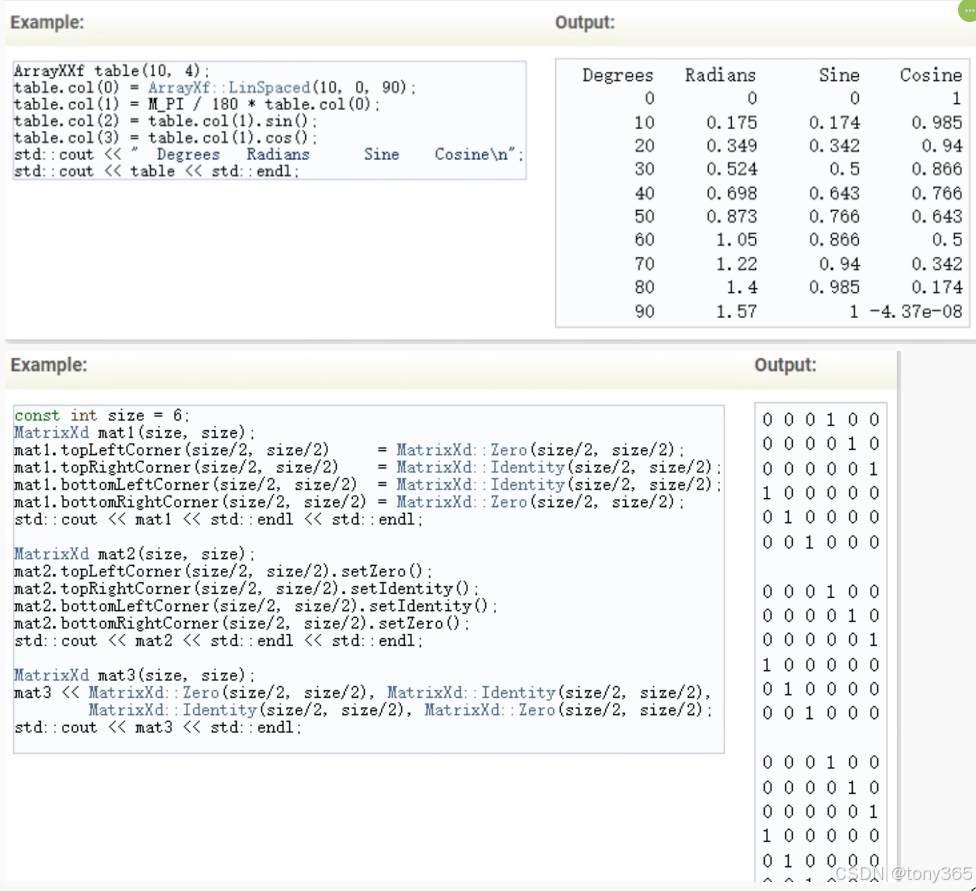
22）一些初始化方法

23） 其他示例

// case1 reduction
// case2 范数
// case3, 按照行或者列进行reduction
// case4: 布尔 all, any, count 操作
// case5: partial recuctions
// case6: broadcasting
// case7: index:A({2, 1}, { 4,2,5,5,3 }) 先索引行，再选列
// case8: reshape 特点是默认按照col优先的储存顺序

#include <iostream>
#include <Eigen/Dense>
#include <algorithm>
using namespace std;
using namespace Eigen;
int main()
{
    // case1 reduction
    Eigen::Matrix2d mat;
    mat << 1, 2,
        3, 4;
    cout << "Here is mat.sum():       " << mat.sum() << endl;
    cout << "Here is mat.prod():      " << mat.prod() << endl;
    cout << "Here is mat.mean():      " << mat.mean() << endl;
    cout << "Here is mat.minCoeff():  " << mat.minCoeff() << endl;
    cout << "Here is mat.maxCoeff():  " << mat.maxCoeff() << endl;
    cout << "Here is mat.trace():     " << mat.trace() << endl;//等价于mat.diagonal().sum()

    // case2 范数
    Eigen::VectorXf v(2);
    Eigen::MatrixXf m(2, 2), n(2, 2);

    v << -1,
        2;

    m << 1, -2,
        -3, 4;

    std::cout << "v.squaredNorm() = " << v.squaredNorm() << std::endl;                      // 所有元素平方后求和
    std::cout << "v.norm() = " << v.norm() << std::endl;                                    // 所有元素平方后求和，再求根
    std::cout << "v.lpNorm<1>() = " << v.lpNorm<1>() << std::endl;                          // 1范数，所有元素绝对值求和
    std::cout << "v.lpNorm<Infinity>() = " << v.lpNorm<Eigen::Infinity>() << std::endl;     // 无穷范数，所有元素的绝对值最大值

    std::cout << std::endl;
    std::cout << "m.squaredNorm() = " << m.squaredNorm() << std::endl;
    std::cout << "m.norm() = " << m.norm() << std::endl;
    std::cout << "m.lpNorm<1>() = " << m.lpNorm<1>() << std::endl;
    std::cout << "m.lpNorm<Infinity>() = " << m.lpNorm<Eigen::Infinity>() << std::endl;


    // case3, 按照行或者列进行reduction
    //Eigen::MatrixXf m(2, 2);
    m << 1, -2,
        -3, 4;

    std::cout << "1-norm(m)     = " << m.cwiseAbs().colwise().sum()
        << " == " << m.colwise().lpNorm<1>() << std::endl;

    std::cout << "infty-norm(m) = " << m.cwiseAbs().rowwise().sum()
        << " == " << m.rowwise().lpNorm<1>() << std::endl;


    // case 4: 布尔 all, any, count 操作
    //all() returns true if all of the coefficients in a given Matrix or Array evaluate to true .
    //any() returns true if at least one of the coefficients in a given Matrix or Array evaluates to true .
    //count() returns the number of coefficients in a given Matrix or Array that evaluate to true.
    Eigen::ArrayXXf a(2, 2);

    a << 1, 2,
        3, 4;

    std::cout << "(a > 0).all()   = " << (a > 0).all() << std::endl;  //1
    std::cout << "(a > 0).any()   = " << (a > 0).any() << std::endl;  //1
    std::cout << "(a > 0).count() = " << (a > 0).count() << std::endl;//4
    std::cout << std::endl;
    std::cout << "(a > 2).all()   = " << (a > 2).all() << std::endl;  //0
    std::cout << "(a > 2).any()   = " << (a > 2).any() << std::endl;  //1
    std::cout << "(a > 2).count() = " << (a > 2).count() << std::endl;//2


    // case5: partial recuctions
    Eigen::MatrixXf mat24(2, 4);
    mat24 << 1, 2, 6, 9,
        3, 1, 7, 2;

    std::cout << "Column's maximum: " << std::endl
        << mat24.colwise().maxCoeff() << std::endl;
    std::cout << "Row's maximum: " << std::endl
        << mat24.rowwise().maxCoeff() << std::endl;

    // case6: broadcasting

    Eigen::MatrixXf matf(2, 4);
    Eigen::VectorXf vf(2);
    matf << 1, 2, 6, 9,
        3, 1, 7, 2;

    vf << 0,
        1;

    //add v to each column of m
    matf.colwise() += vf;

    std::cout << "Broadcasting result: " << std::endl;
    std::cout << matf << std::endl;

    // case7: index

    Eigen::MatrixXi A = Eigen::MatrixXi::Random(4, 6);
    cout << "Initial matrix A:\n" << A << "\n\n";
    cout << "A(all,{4,2,5,5,3}):\n" << A(Eigen::all, { 4,2,5,5,3 }) << "\n\n";
    cout << "A({2,1},{4,2,5,5,3}):\n" << A({2, 1}, { 4,2,5,5,3 }) << "\n\n";


    // case8: reshape 特点是默认按照col优先的储存顺序
    // m.reshaped<RowMajor>().transpose()   按照行顺序重新排列为1D linear. 然后转置


    // stl 应用2D arrays或matrices. 比如对行或者列进行排序

    A = ArrayXXi::Random(4, 4);
    cout << "initial array A:" << A << "\n";
    for (auto row : A.rowwise()) {
        cout << row << endl;
        std::sort(row.begin(), row.end());
    }
    cout << "sort row array A:" << A << "\n";

    for (auto col : A.colwise()) {
        
        std::sort(col.begin(), col.end());
    }
    cout << "sort col array A:" << A << "\n";

24）最小二乘法解线性方程组

下面两种方法分别是QR分解和正则化的方法求解，后者速度更快精度略低。

A.colPivHouseholderQr().solve(b)
(A.transpose()*A).ldlt().solve(A.transpose()*b)