背包问题是动态规划的经典问题，最近刷题又复习了一遍，本文再梳理一下01背包、完全背包及多重背包问题。

一、 01背包问题

• 经典01背包问题
  01背包问题：给定n个物品，每个物品的重量为wi，价值为vi， 现给定一个容量为w的背包，要求在背包容量的限定条件下，尽可能装价值多的物品（背包不一定要装满）。

  对于该问题其实可以使用深度遍历的方法暴力搜索，对于每个物品均有两种状态：选取或放弃。但这种方式复杂度高达$\sigma (2^n)$。为此，我们可以采用动态规划的方式求解,动态规划最重要的是状态转移方程，01背包的状态转移方程如下所示
  $f[i][j]=max(f[i-1][j],f[i-1][j-w_i]+v_i)$

  从公式可以看出，对每一个位置 $f[i][j]$的求解仅仅需要知道上一行的状态，因此一般为了节约空间可以反复使用一维数组进行求值，这在动态规划里叫滚动数组，但是需要注意的是我们是从后往前更新，而不是从前往后更新，这样做保证了更新当前状态时，它所依赖的两个状态还没有被修改。

int weight[200], value[200], f[100]; //f为滚动数组
int main() {
   int n, w; cin >> n >> w;
   for (int i = 1; i <= n; i++)
   		cin >> weight[i] >> value[i];

   for (int i = 1; i <= n; i++)
   		for (int j = w; j >= weight[i]; j--)
   			f[j] = max(f[j], f[j - weight[i]] + value[i]);
   cout << "背包能放的最大价值为:" << f[w] << endl;
   return 0;
}

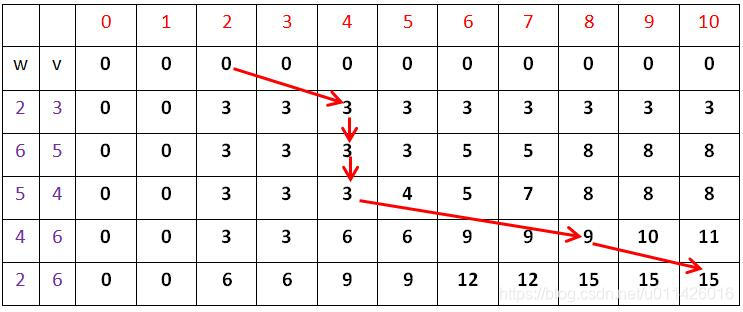
图解：物件物品如下图左侧两列所示，背包容量为10，红色箭头指示装包方案

• 背包装满求最大价值
  仔细看图你会发现上述问题中对于给定的容量为10的背包其实并没装满，分别装入了（2,3）（4,6）（2,6）三个物品，总重量为2+4+2 = 8 < 10。那么，如果我们要求装满背包又该如何操作呢？

  我们考虑前i个物品装容量为j的背包这一问题，其实就是状态方程中的$f[i][j]$，我们现在要考虑第i个物品是否要装进背包，如状态转移方程所示，第i个物品要不要装进去。

  1） 如果物品$i$要装进背包，那么需要装满容量为$j$的背包，也就意味着$f[i-1][j-w_i]$，前$i-1$个物品一定能装满容量为$j-w_i$的背包；

  2） 如果物品$i$不装进背包，那么前$i-1$个物品本身就能装满容量为$j$的背包

  上述两个条件至少满足一个就可以得到$f[i][j]$的解，如果上述两条件均不满足，即无论装不装第$i$个物品，背包都装不满，那么如何表示装不满呢？我们将这个状态的值置为无穷小$-\infty$，表示无解。无论装不装第$i$个物品，背包都装不满，也就意味着$f[i-1][j]$和$f[i-1][j-w_i]$均为$-\infty$，无解。

  因为这里我们自底向上求解，实际编程中，只需要在初始化阶段做点事情即可，具体地，我们只需要对滚动数组$f[0]=0$， 而其他值均值为$-\infty$即可，表示初始状态，只有前0个物品放入容量为0的背包是装满的状态，而其他都是无法装满的状态即无解。后续的求解，会依赖之前的状态，如果之前的状态均无解，那么当前状态也无解。

int weight[200], value[200], f[100]; //f为滚动数组
int main() {
	int n, w; cin >> n >> w;
	for (int i = 1; i <= n; i++)
		cin >> weight[i] >> value[i];
	for (int i = 1; i <= w; i++)
		f[i] = INT_MIN;
	
	for (int i = 1; i <= n; i++) {
		for (int j = w; j >= weight[i]; j--)
			f[j] = max(f[j], f[j - weight[i]] + value[i]);
	}
	cout << "背包装满的最大价值为:" << f[w] << endl;
	return 0;
}

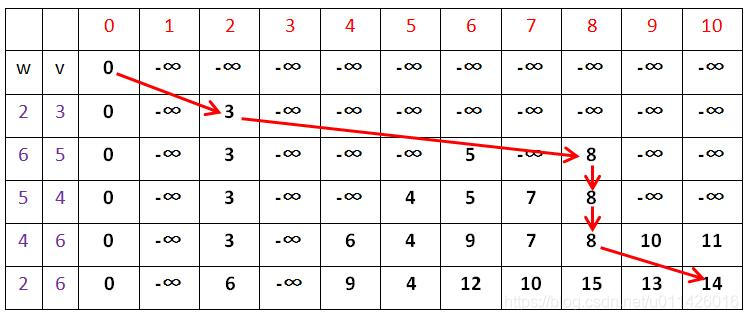
图解：物件物品如下图左侧两列所示，背包容量为10，要求装满，红色箭头指示装包方案

• 背包装满求最小价值
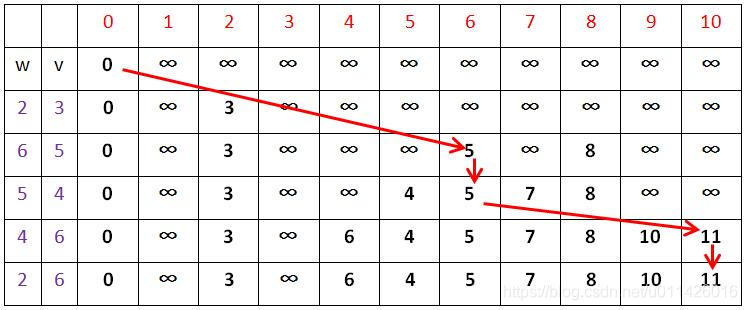
  同理，我们只需要在初始化时将滚动数组$f[0]=0$， 而其他值均值为$\infty$即可。

int weight[200], value[200], f[100];
int main() {
	int n, w; cin >> n >> w;
	for (int i = 1; i <= n; i++)
		cin >> weight[i] >> value[i];
	for (int i = 1; i <= w; i++)
		f[i] = INT_MAX;

	for (int i = 1; i <= n; i++) {
		for (int j = w; j >= weight[i]; j--)
			f[j] = min(f[j], f[j - weight[i]] + value[i]);
	}
	cout << "背包装满的最小价值为:" << f[w] << endl;
	return 0;
}

二、完全背包问题

完全背包问题跟01背包不同的是，每种物品可以选择多件。常见的代码有两种写法：method1和method2.

int weight[200], value[200], f[100], n, w;
void method1(){
	for (int i = 1; i <= n; i++)
		for (int j = w; j >= weight[i]; j--)
			for (int k = 1; k * weight[i] <= j; k++)
				f[j] = max(f[j], f[j - k*weight[i]] + k*value[i]);
}

void method2(){
	for (int i = 1; i <= n; i++)
		for (int j = weight[i]; j <= w; j++)
			f[j] = max(f[j], f[j - weight[i]] + value[i]);
}

int main() {
	cin >> n >> w;
	for (int i = 1; i <= n; i++)
		cin >> weight[i] >> value[i];
	method1();
	//method2();
	cout << "背包能放的最大价值为:" << f[w] << endl;
	return 0;
}

1） method1较好理解，每种物品可以选0,1,2,3…多个，那么最多可以选几个呢？ 对于第$i$中物品而言，要装进容量为$j$的背包，那么最多可以装$\lfloor j/w_i\rfloor$个，因此假设用k表示个数的话，$0\le k\le \lfloor j/w_i\rfloor$， 跟01背包不同的是，01背包中的k只能取0或1.这里多了一重循环，取遍所有可以取的$k$值。
状态转移方程为：
$$f[i][i]=\{\begin{array}{ll}0& i=0||j=0\\ max(f[i-1][j-k\times w_i]+k\times v_i& 0\le k\le \lfloor j/w_i\rfloor \end{array}$$

最坏情况下复杂度为 $\sigma (n{W}^2)$ , 不够好。这里面还是有很多多余的重复计算。第三层循环里，对于每种物品，都计算$\lfloor j/w_i\rfloor$次，这是不必要的。动态规划就是要利用已经计算过的小规模的问题的解，来求解更大规模的问题的解。让我们来探寻一下，还有什么我们没有利用的重复计算。

再重申一下，$dp[i][j]$:=从前i种物品中挑选总重量不超过j的物品的最大总价值。
再来看一下上面的递推公式,这里的k可分为两种情况，$k=0$ 和 $k̸=0$,也就是第i种物品不选，或者至少选1个。这里的k可分为两种情况，$k=0$ 和 $k̸=0$,也就是第$i$种物品不选，或者至少选1个。

• $k=0$时，即不选择第i种物品，$dp[i][j]=dp[i-1][j]$
• $k̸=0$时，即至少选一个第i种物品，$dp[i][j]=dp[i][j-w_i]+v[i]$
  注意上面红色标识的 $i-1$ 和$i$。
  $k=0$时，比较容易理解，$k̸=0$时，先强行往背包里塞一个第i种物品，然后把问题转化成更小规模的问题。$k=0$时，比较容易理解，$k̸=0$时，先强行往背包里塞一个第$i$种物品，然后把问题转化成更小规模的问题。
  $i$和$j$都是按递增顺序循环的，所以求解$dp[i][j]$时，$dp[i][j-w_i]$的值是已经求过了的，可以直接拿来用。$i$和$j$都是按递增顺序循环的，所以求解$dp[i][j]$时，$dp[i][j-w_i]$的值是已经求过了的，可以直接拿来用。
  综上，可以得出递推公式：
  $dp[i][j]=max(dp[i-1][j],dp[i][j-w_i]+v[i])$
  这即是method2的状态转移方程。

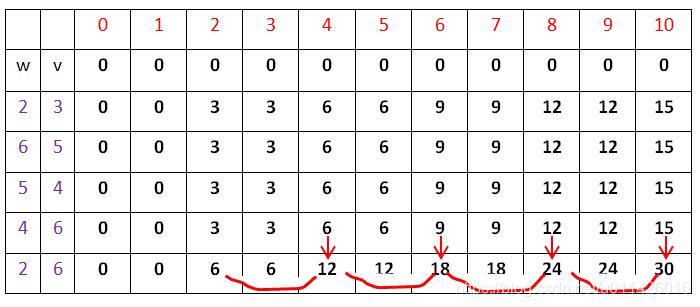
最后也上图一张，红色线条和箭头表示求解的依赖项。

这一部分引用自：https://blog.csdn.net/yoer77/article/details/70943462， 感谢原作者！

三、多重背包问题

相对于完全背包问题，多重背包问题对于每件物品的数量有所限定，如给定三件物品，背包容量为5的问题，接下来三行每一行分别表示物品的重量、价值和数量。那么最优解为第一种物品取2个，第二种物品取0件，第三种物品取2件，最大价值为6+2*20 = 46.
3 5
1 6 10
2 10 5
2 20 13

对于该问题，依然可以采用完全背包的第一种解法求解，只是这里的k值的取值范围为：$k=min(num[i],\lfloor j/w_i\rfloor )$，因此第一种解法的代码为：

int weight[2000], value[2000], num[2000], f[1000], n, w;
void multiPack(){
	for (int i = 1; i <= n; i++)
		for (int j = w; j >= weight[i]; j--)
			for (int k = 1; k * weight[i] <= j && k <= num[i]; k++)
				f[j] = max(f[j], f[j - k*weight[i]] + k*value[i]);
}

int main() {
	cin >> n >> w;
	for (int i = 1; i <= n; i++)
		cin >> weight[i] >> value[i] >> num[i];
	multiPack();
	cout << "背包能放的最大价值为:" << f[w] << endl;
	return 0;
}

这种解法的复杂度略高，背包九讲推荐的解法将每件物品的数量num进行二进制拆分，当然需要注意的是拆分的各个数字能组成1-num之间的任意数字。如13需要拆分为1,2,4,6它可以组成1,2,3,4,5,6,7,8,9,10,11,12,13所有数字，当然0也可以，就是全部不选的情况。这里的拆分是将k从1开始不断翻倍，直到k > num，那么最后一个数字就是num-k.最后转换为经典的01背包问题求解。代码如下：

int weight[2000], value[2000], f[1000], n, w, tot;
int main() {
	cin >> n >> w;
	int w_, v_, num;
	for (int i = 1; i <= n; i++){
		cin >> w_ >> v_ >> num;
		int k = 1;
		while (num >= 0){
			weight[++tot] = k <= num ? k*w_ : num*w_;
			value[tot]  = k <= num ? k*v_ : num*v_;
			num -= k;
			k *= 2;
		}
	}
	for (int i = 1; i < tot; i++)
		for (int j = w; j >= weight[i]; j--)
			f[j] = max(f[j], f[j - weight[i]] + value[i]);
	cout << "背包能放的最大价值为:" << f[w] << endl;
	return 0;
}