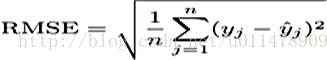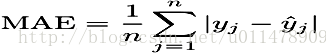数据挖掘函数之回归（regression）

回归是一种用来预测连续数值的数据挖掘函数。利润，销售，抵押贷款利率，房价，面积，温度，距离都可以使用这种回归函数来预测。例如，一个回归模型基于地理位置，房间数，面积大小和其他一些因素来预测房价。

一个回归任务开始于一个目标值已知的数据集。例如，一个预测房价的模型基于一段时间内很多房子的数据开发出来。除了一些简单的数值，房价可能会跟房子的年龄，面积，房间数，税，是否靠近购物中心等等一系列因素有关。因此，房子的价值成为了目标，其他的属性成为了预测因子，而且每一个房子的数据都组成了一条记录。

在模型建立的过程中，回归就为build data中的每一条记录用预测因子函数估算目标值。预测因子和目标值的关系在模型中被总结出来，然后这个模型就可以被应用到目标值不确定的各种各样的数据集上。

一个回归工程的历史数据通常分为两个数据集：一个用于创建模型，另一个用于测试模型预测值和实际值的差异。

回归模型应用于各种趋势分析，业务规划，市场营销，财务预测，生物医学等等一系列领域。

回归模型是如何工作的？

为数据挖掘开发和使用高质量的回归模型并不需要懂得回归中用到的数学知识。但是，懂一点基础概念还是有帮助的。

回归为了使归回函数最佳拟合一组观测数据去寻找一个参数的值来达到此目的。下面的公式用符号表示出了这种关系。

y = F(x,a)  + e

y为需要预测的目标，F函数有着一个或多个预测因子，记为x，斜率为a,误差为e。

线性回归

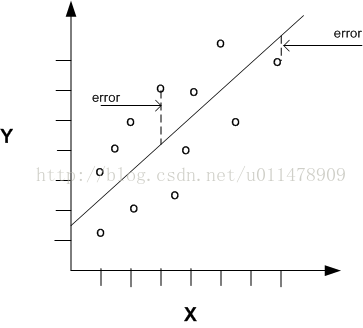
线性回归当预测因子和目标值之间的关系可以近似用直线表示时可以使用。只有一个预测因子的回归是可视化的。一个简单的线性回归如下如所示。

公式为： y = a2x   +  a1  + e 

参数意义如下：

线的斜率a2  ------ 一个数据点与回归线之间的角度大小。

Y轴的截距a1

多元线性回归

多元线性回归指的是有两个或两个以上预测因子的线性回归（x1,x2,....,xn）。当多个预测因子被使用到时，回归线将无法在二元空间可视化。

y = a1 +  a2 x1  +  a3 x2   + .....  + an  xn-1  + e 

回归系数

在多元线性回归中回归参数通常被称为回归系数。当你建立一个多元线性回归模型的时候，算法将为模型使用到的每一个预测因子计算回归系数。回归系数的大小就是预测因子x对预测目标y的影响程度的大小。

想要分析回归系数，须要用大量的统计信息才能评判回归线与数据的拟合度。

非线性回归

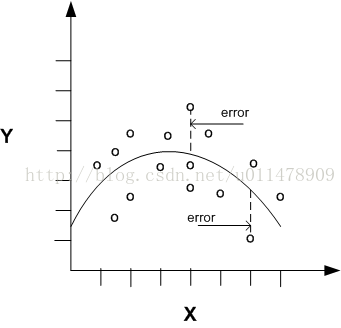
通常x和y的关系无法近似为一条直线。这种情况就需要使用非线性回归技术了。而且为了使数据具有线性关系，需要对数据进行预处理。

如上图所示，单预测因子的非线性回归

多元非线性回归

多元线性回归指的是拥有两个或两个以上的预测因子的回归模型。当多个预测因子被使用到时，回归线将无法在二元空间可视化。

置信区间

回归模型预测评分数据中的每组案例的数字值目标。除了预测之外，一些回归算法可以确定置信区间。

当建立一个模型时给定了一个置信度，置信区间将会随着预测产生。例如，一个模型预测一栋房子的价格是500000美元的置信度为95%，置信区间为475000美元到525000美元。

回归模型的检验

回归模型被应用到一些已知目标值的测试数据上，然后对预测出来的数据与已知的数据进行比较。

测试数据必须与建模时用的数据兼容。通常情况下，建立数据和测试数据来自同一个历史数据集。记录的一部分被用来建立模型，另一部分被用来测试模型。

模型的测试为了评估模型预测的准确性。如果模型具有很好的性能，满足业务需求，那么他就可以预测到新的数据来预测未来。

回归统计

均方根误差和平均绝对误差经常被用作统计信息来评价回归模型的质量。不同的统计数据。不同的统计信息也取决于算法中使用的回归方法。

均方根误差

均方根误差的就是预测值减去实际值然后平方再开根号。数学表达式如下：

SQRT(AVG((predicted_value - actual_value) * (predicted_value - actual_value)))

也可由如下公式表示：

平均绝对误差

平均绝对误差就是预测的值减去实际值得绝对值然后求平均数。数学表达式如下：

AVG(ABS(predicted_value - actual_value))

也可由如下公式表达：