智能优化算法应用:基于秃鹰算法优化的最小交叉熵图像多阈值分割
摘要:本文介绍基于最小交叉熵的图像分割,并且应用秃鹰算法进行阈值寻优。
1.前言
阅读此文章前,请阅读《图像分割:直方图区域划分及信息统计介绍》https://blog.csdn.net/u011835903/article/details/108024753 了解基础知识,相关公式含义。
2.最小交叉熵阈值分割原理
1993 年,Li等人将交叉熵的概念引入到图像处理领域,提出了基于一维灰度级直方图的最小交叉熵阈值选取方法。该方法以分割后的图像与原图像的信息量差异最小为阈值选取准则,实质上是使分割前后图像的Kullback散度达到最小。交叉熵的计算公式为:
H
(
t
)
=
∑
i
=
0
t
i
h
i
l
n
i
u
0
(
t
)
+
∑
i
=
t
+
1
L
−
1
i
h
i
l
n
i
u
b
(
t
)
(1)
H(t) = \sum_{i=0}^t ih_iln\frac{i}{u_0(t)} + \sum_{i=t+1}^{L-1} ih_iln\frac{i}{u_b(t)} \tag{1}
H(t)=i=0∑tihilnu0(t)i+i=t+1∑L−1ihilnub(t)i(1)
使式(1)取最小值的t值即为最佳阈值:
t
∗
=
a
r
g
m
i
n
(
0
≤
t
≤
L
−
1
)
{
H
(
t
)
}
(2)
t^*=argmin_(0\leq t\leq L-1)\{H(t)\} \tag{2}
t∗=argmin(0≤t≤L−1){H(t)}(2)
推广到多阈值则为,寻找一组阈值
(
t
0
,
.
.
.
,
t
n
)
(t_0,...,t_n)
(t0,...,tn)使得熵值最小:
t
(
1
,
.
.
,
n
)
∗
=
a
r
g
m
i
n
{
H
0
+
H
1
+
,
.
.
.
+
H
n
}
(3)
t(1,..,n)^*=argmin\{H_0+H_1+,...+H_n\}\tag{3}
t(1,..,n)∗=argmin{H0+H1+,...+Hn}(3)
3.基于秃鹰优化的多阈值分割
由上述交叉熵分割法的原理可知,要得到最终的阈值,需要去寻找阈值,熵值最小。于是可以利用智能优化算法进行阈值的寻优,使得获得最佳阈值。
于是优化的适应度函数就是:
f
u
n
{
t
(
1
,
.
.
,
n
)
∗
}
=
a
r
g
m
i
n
{
H
0
+
H
1
+
,
.
.
.
+
H
n
}
(4)
fun\{t(1,..,n)^*\}=argmin\{H_0+H_1+,...+H_n\}\tag{4}
fun{t(1,..,n)∗}=argmin{H0+H1+,...+Hn}(4)
设置阈值分割的个数,寻优边界为0到255(因为图像的像素值范围为0-255),设置相应的秃鹰算法参数
秃鹰算法原理请参考:https://blog.csdn.net/u011835903/article/details/113775430
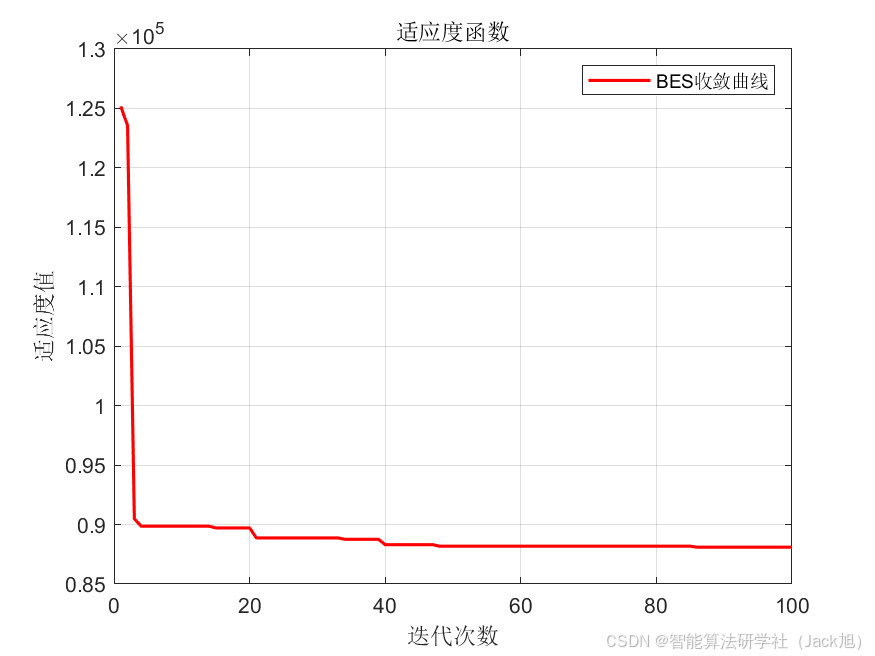
4.算法结果:
5.参考文献:
[1]吴一全,孟天亮,吴诗婳.图像阈值分割方法研究进展20年(1994—2014)[J].数据采集与处理,2015,30(01):1-23.