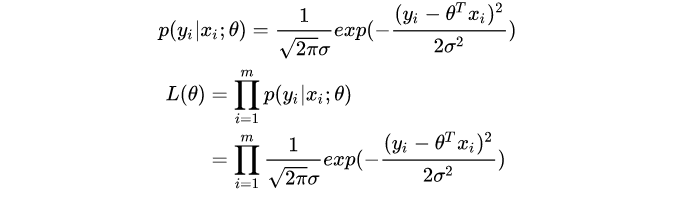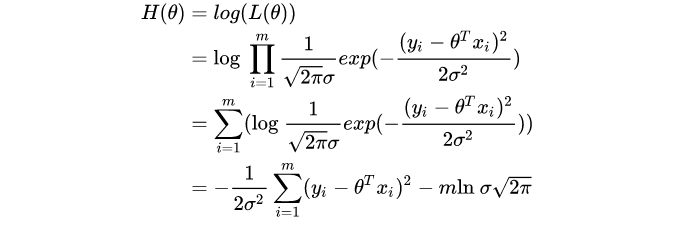机器学习 EM算法理解

文章目录

前言
极大似然
EM算法
参考

前言

EM算法与极大似然算法相似，是一种解决问题的思想，解决一类问题的框架，和线性回归，逻辑归回，决策树等一些具体算法不同，极大似然算法更加抽象，是很多具体算法的基础。本文主要从一个例子出发，从极大似然到EM算法。本文主要参考：人人都能看懂EM算法。

极大似然

问题描述

假设当前有个任务：调查一所学校的学生的身高分布。该如何调查？首先先假设这所学校学生的身高服从正态分布 $N(\mu, \sigma^2)$ ，极大似然估计需要先假设数据的总体分布。该分布中 $\mu$ 和 $\sigma$ 为未知项，假设得到这两个结果，那么将得到最终的学校学生身高分布。

要估算这个这个分布的两个参数，不可能全部学生都需要统计，那么就需要用到抽样，概率统计的思想，根据样本估算总体。假设随机抽取200人身高（下面简述为人），那么可以根据这200人，得到样本的的均值 $\mu$ 和方差 $\sigma$ 。

将上面的过程用数学语言描述就是：为了统计学校学生的身高分布，独立地按照概率密度函数 $p(x|\theta)$ 抽取200人，组成样本集合： $X=x_1, x_2, ..., x_N$ ，其中 $x_i$ 表示第 $i$ 人的身高， $N$ 表示抽样样本数200。然后通过样本集 $X$ 来估算总体的未知参数 $\theta$ 。这里的概率密度函数 $p(x|\theta)$ 服从高斯分布 $N(\mu, \sigma^2)$ ，其中未知参数是 $\theta=[\mu, \sigma]^T$ 。现在的任务就是需要估计总体参数 $\theta$ 。

参数估计

根据随机抽样的原理，这200名学生是随机抽样的，相互独立。那么假设抽到学生A的概率是 $p(x_A|\theta)$ ，抽到学生B的概率是 $p(x_B|\theta)$ ，那么同时抽到学生A和学生B的概率就为： $p_A*p_B$ ，同理抽到这200位学生的概率就是各自概率的乘积，即联合概率，用下式表示：
$L(\theta) = L(x_1, x_2, ..., x_n;\theta) = \prod^{n}_{i=1}p(x_i|\theta), \theta \in \Theta$ $n$ 表示的是抽样样本数，这个公式反映了，在概率密度函数的参数为 $\theta$ 时，得到 $X$ 这组样本的概率。换言之 $L$ 是关于 $\theta$ 的函数。这个函数反映了在不同参数 $\theta$ 的取值下，取得当前样本集的可能性，因此称为参数 $\theta$ 的相对于样本集 $X$ 的似然函数，记为 $L(\theta)$ 。

将上式变形，两边取对数，则为： $H(\theta) = \ln L(\theta) = \ln \prod^{n}_{i=1}p(x_i|\theta) = \sum^{n}_{i=1}\ln p(x_i|\theta)$ 这里取对数的原因是将累积变成累加，方便计算。

那么在这所学校中，要使得抽到这200人的概率最大，那么就要让对应的似然函数 $L(\theta)$ 极大，即： $\hat{\theta} = arg maxL(\theta)$ ，这里的 $\hat{\theta}$ 叫做 $\theta$ 的极大似然估计量，即所求的值。

怎么样求极大值，高中的时候学过的偏导数，就可以求得一个函数的极大值。

极大似然估计

在现实场景下，大多数情况根据已知条件去推算结果，而极大似然估计可以这么理解为相反，根据结果，寻找使该结果出现可能性极大的条件，以此作为估计值。
如：

假如一个学校的学生男女比例为 9:1 (条件)，那么你可以推出，你在这个学校里更大可能性遇到的是男生 (结果)；
假如你不知道那女比例，你走在路上，碰到100个人，发现男生就有90个 (结果)，这时候你可以推断这个学校的男女比例更有可能为 9:1 (条件)，这就是极大似然估计。

极大似然估计，只是一种概率论在统计学的应用，它是参数估计的方法之一。说的是已知某个随机样本满足某种概率分布，但是其中具体的参数不清楚，通过若干次试验，观察其结果，利用结果推出参数的大概值。极大似然估计是建立在这样的思想上：已知某个参数能使这个样本出现的概率极大，我们当然不会再去选择其他小概率的样本，所以干脆就把这个参数作为估计的真实值。

求解极大似然的一般步骤如下：

写出似然函数
对似然函数取对数，并整理
求导数，令导数为0，得到似然方程
解似然方程，得到参数

极大似然应用

极小化代价函数

极小化代价函数也可以理解为回归问题中的极小化平方和。假设线性回归模型具有如下形式： $\sum^{d}_{i=1}\theta_jx_j+\epsilon = \theta^{T}+\epsilon$ 其中 $x\in R^{1\times d}$ ， $\theta\in R^{1\times d}$ ，误差 $\epsilon\in R$ 。那么如何求 $\theta$ ?

最小二乘法估计。最合理的参数估计量应该是的模型能最好地拟合样本数据，也就是估计值和观测值只差的平方和最小，推导过程如下： $J(\theta) = \sum^{n}_{i=1}(h_\theta(x_i)-y_i)^2$ 求解方法是通过梯度下降算法，训练数据不断迭代得到最终的值。
极大似然方法，最合理的参数估计量应该使得从模型中抽取 $m$ 组样本观测值的概率极大，即似然函数极大。
假设误差项 $\epsilon\in N(0, \sigma^2)$ ，则 $y_i\in N(\theta x_i, \sigma^2)$ 。

在这里插入图片描述

EM算法

EM算法与极大似然相似的地方是假设总体数据都满足某一个分布，如正态分布。不一样的是假设学校中男生和女生分别服从两种不同的正态分布，即男生的分布为 $N(\mu_1, \sigma^2_1)$ ，女生的分布为 $N(\mu_2, \sigma^2_2)$ 。用数学的语言就是，抽取得到的每个样本都不知道是从哪个分布来的。那怎么办呢？
在这里插入图片描述

EM算法推导

基础知识

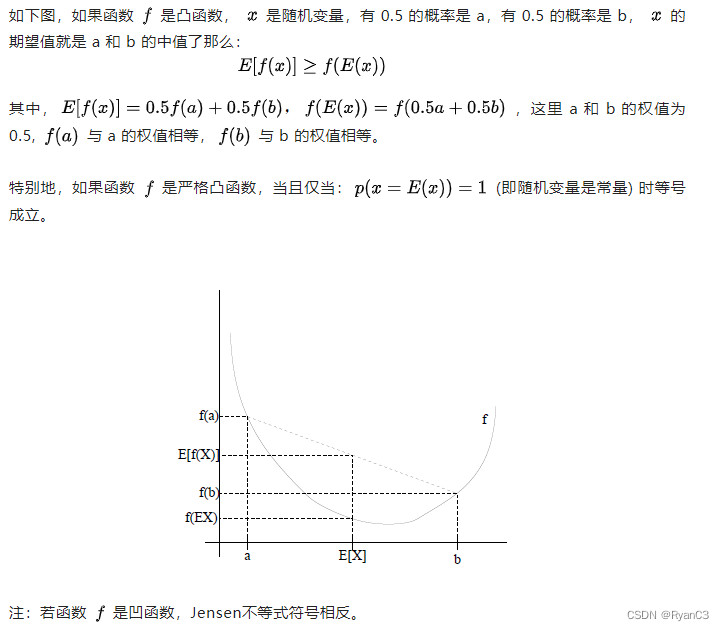
凸函数

在这里插入图片描述

Jensen不等式

在这里插入图片描述

期望

在这里插入图片描述

推导过程

在这里插入图片描述

算法流程

在这里插入图片描述

另一种呢理解

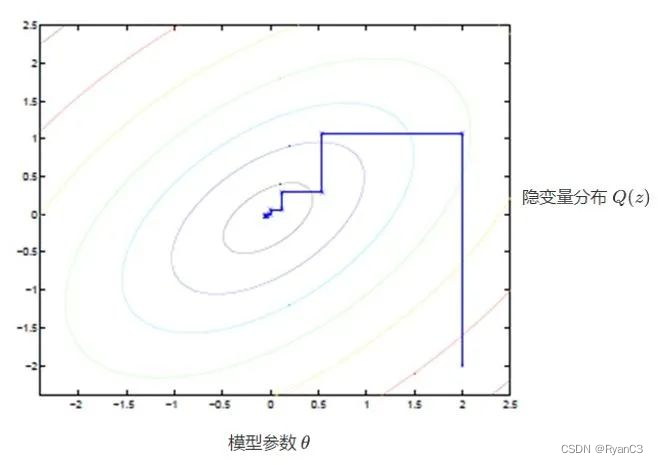
坐标上升法（Coordinate ascent）(类似于梯度下降法，梯度下降法的目的是最小化代价函数，坐标上升法的目的是最大化似然函数；梯度下降每一个循环仅仅更新模型参数就可以了，EM算法每一个循环既需要更新隐含参数和也需要更新模型参数，梯度下降和坐标上升的详细分析参见攀登传统机器学习的珠峰-SVM (下))

在这里插入图片描述

图中的直线式迭代优化的路径，可以看到每一步都会向最优值前进一步，而且前进路线是平行于坐标轴的，因为每一步只优化一个变量。这犹如在x-y坐标系中找一个曲线的极值，然而曲线函数不能直接求导，因此什么梯度下降方法就不适用了。但固定一个变量后，另外一个可以通过求导得到，因此可以使用坐标上升法，一次固定一个变量，对另外的求极值，最后逐步逼近极值。对应到EM上，E步：固定 θ，优化Q；M步：固定 Q，优化 θ；交替将极值推向极大。

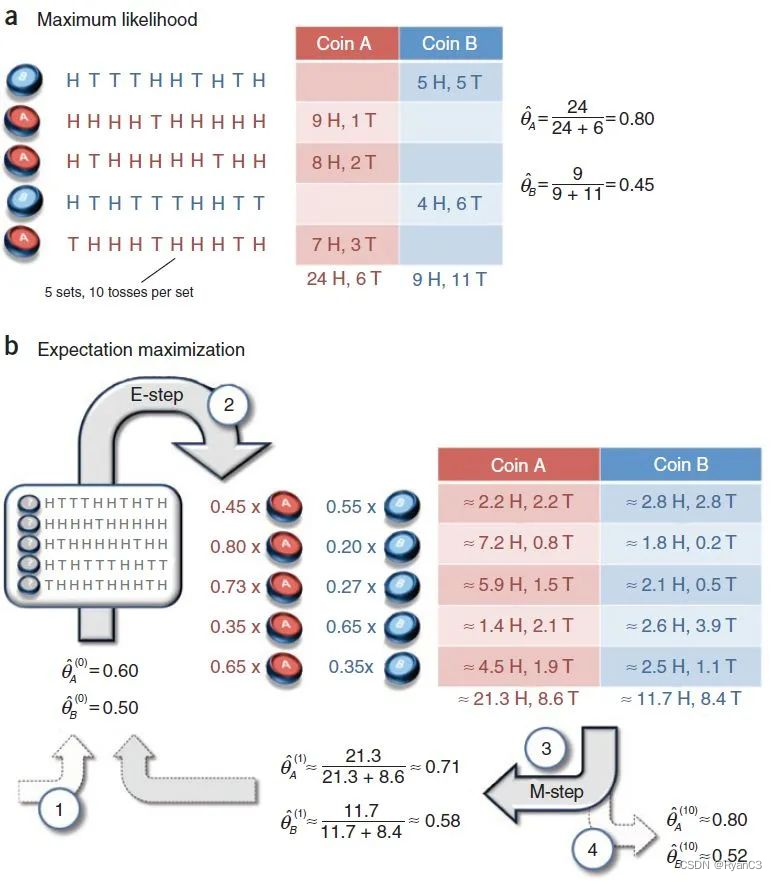
EM算法案例

假设有两枚硬币A、B，以相同的概率随机选择一个硬币，进行如下的掷硬币实验：共做 5 次实验，每次实验独立的掷十次，结果如图中 a 所示，例如某次实验产生了H、T、T、T、H、H、T、H、T、H (H代表正面朝上)。a 是在知道每次选择的是A还是B的情况下进行，b是在不知道选择的是A还是B的情况下进行，问如何估计两个硬币正面出现的概率？
在这里插入图片描述