神经网络（全连接）的前向和反向传播

转自我的知乎专栏：https://zhuanlan.zhihu.com/p/34378516/edit

神经网络模型是人工智能最基础的模型，它的诞生也是受益于神经科学家对猫的大脑的研究。神经网络通过自学习的方式可以获得高度抽象的，手工特征无法达到的特征，在计算机视觉领域取得了革命性的突破。而神经网络之所以最近几年取得了这么大的成功，反向传播算法是一个很重要的原因。可以说，只有深入了解了反向传播算法才可以说真正了解了神经网络的作用过程。
本文尽量用图文并茂的方式讲清楚神经网络的前向和反向传播，并用python做了实现。希望能以最易懂的方式讲清楚这两个东西。至于神经网络的基本构成，如权重，偏置，激活函数，随机梯度下降等基础概念就不再细述，读者可以百度。要理解反向传播，必须得知道偏导数的数学定义，要看懂代码得有一定的python基础，最好对numpy也有一定了解。废话不多说，以下是正文。
首先构建一个最简单的神经网络如下。
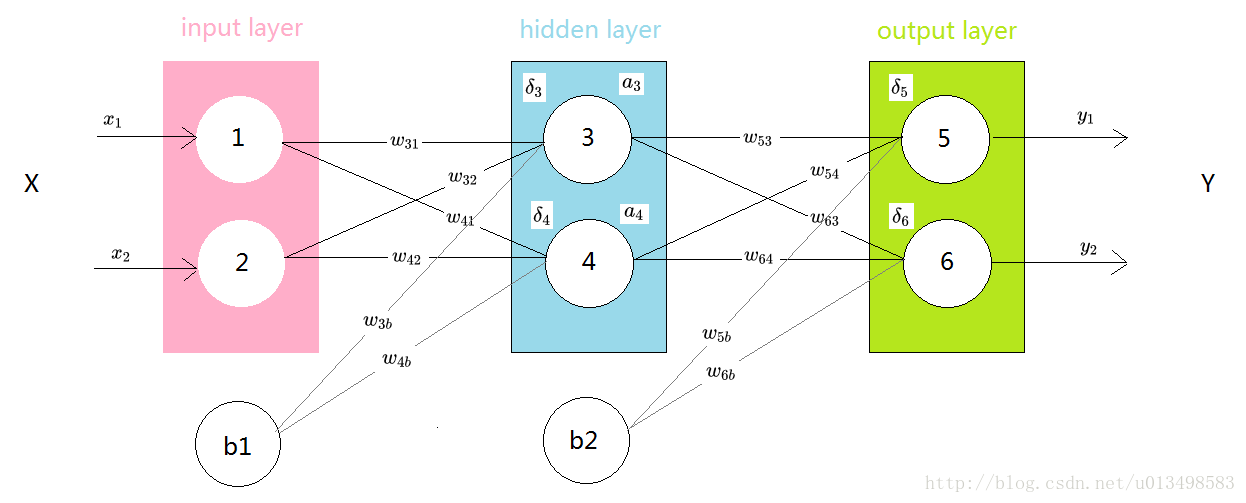
这里写图片描述
所谓全连接，就是指第N层的每个神经元和第N-1层的每个神经元都相连，每个连接都有一个权值。
如上图，输入层有2个节点，编号依次为1,2；隐藏层也有两个节点，编号分别为3,4；输出层也是两个节点，编号为5,6。b1和b2是偏置节点。
其中的符号含义为：
$w_{ji}$ 表示第j个节点（位于第N层的非偏置节点）和第i个节点（位于第N-1层的非偏置节点）之间的权重。j是目标节点，i是源节点。
$w_{jb}$ 表示第j个节点（位于第N层的非偏置节点）和位于上一层的偏置节点之间的权重。
$a_{j}$ 表示第j个节点的输出值。
激活函数假定为sigmoid，当然也可以用relu等。sigmoid函数的定义为：

s i g m o i d (x) = 1 1 + e - x

$sigmoid(x) = \frac{1}{1+e^{-x}}$
为了方便演示，我们给一些实际数据，假定输入数据

x1=0.02,x2=0.04 x 1 = 0.02 , x 2 = 0.04 $x_{1} = 0.02 ,x_{2} = 0.04$ ；期望输出也就是目标值为

t1=0.5,t2=0.9 t 1 = 0.5 , t 2 = 0.9 $t_{1} = 0.5, t_{2} = 0.9$ 。
权重w的初始化有很多方法，比如xaiver，msra等，这里就任意赋值了，假定初始化为

w31=0.05,w32=0.1,w41=0.15,w42=0.2,w53=0.25,w54=0.3,w63=0.35,w64=0.4 w 31 = 0.05 , w 32 = 0.1 , w 41 = 0.15 , w 42 = 0.2 , w 53 = 0.25 , w 54 = 0.3 , w 63 = 0.35 , w 64 = 0.4 $w_{31} = 0.05 , w_{32} = 0.1 , w_{41} = 0.15 , w_{42} = 0.2 , w_{53} = 0.25 , w_{54} = 0.3 , w_{63} = 0.35 , w_{64} = 0.4$
偏置项初始化为

b1=0.5,b2=0.9 b 1 = 0.5 , b 2 = 0.9 $b_{1} = 0.5 , b_{2} = 0.9$

w3b=0.5,w4b=0.5,w5b=0.9,w6b=0.9 w 3 b = 0.5 , w 4 b = 0.5 , w 5 b = 0.9 , w 6 b = 0.9 $w_{3b} = 0.5 , w_{4b} = 0.5 , w_{5b} = 0.9 , w_{6b} = 0.9$

前向传播

前向传播比较简单，就是向量点乘，也就是加权求和，然后经过一个激活函数。

y = w * x + b

$y = w*x + b$
以节点3为例，节点3的输入值为

w31x1+w32x2+w3bw31x1+w32x2+w3b w 31 x 1 + w 32 x 2 + w 3 b w 31 x 1 + w 32 x 2 + w 3 b $w_{31} x_{1}+w_{32} x_{2} + w_{3b}w_{31} x_{1}+w_{32} x_{2} + w_{3b}$
节点3的输出值为

a3=sigmoid(w31x1+w32x2+w3b)a3=sigmoid(w31x1+w32x2+w3b) a 3 = s i g m o i d ( w 31 x 1 + w 32 x 2 + w 3 b ) a 3 = s i g m o i d ( w 31 x 1 + w 32 x 2 + w 3 b ) $a_{3} = sigmoid(w_{31} x_{1}+w_{32} x_{2} + w_{3b})a_{3} = sigmoid(w_{31} x_{1}+w_{32} x_{2} + w_{3b})$
实际值为

a3=sigmoid(0.05∗0.02+0.1∗0.04+0.5)=11+e−0.505=0.6236336 a 3 = s i g m o i d ( 0.05 ∗ 0.02 + 0.1 ∗ 0.04 + 0.5 ) = 1 1 + e − 0.505 = 0.6236336 $a_{3} = sigmoid(0.05*0.02+0.1* 0.04 + 0.5) = \frac{1}{1+e^{-0.505}} = 0.6236336$
同样的节点4的输出值为

a4=sigmoid(w41x1+w42x2+w4b) a 4 = s i g m o i d ( w 41 x 1 + w 42 x 2 + w 4 b ) $a_{4} = sigmoid(w_{41} x_{1}+w_{42} x_{2} + w_{4b})$
实际值为

a4=sigmoid(0.15∗0.02+0.2∗0.04+0.5)=11+e−0.011=0.50274997 a 4 = s i g m o i d ( 0.15 ∗ 0.02 + 0.2 ∗ 0.04 + 0.5 ) = 1 1 + e − 0.011 = 0.50274997 $a_{4} = sigmoid(0.15*0.02+0.2* 0.04 + 0.5) = \frac{1}{1+e^{-0.011}} = 0.50274997$
节点5的输出值为

a5=sigmoid(w53a3+w54a4+w5b) a 5 = s i g m o i d ( w 53 a 3 + w 54 a 4 + w 5 b ) $a_{5} = sigmoid(w_{53} a_{3}+w_{54} a_{4} + w_{5b})$
实际值为

y 1 = a 5 = s i g m o i d (0.25 * 0.6236336 + 0.35 * 0.50274997 + 0.9) = 1 1 + e 1.2318708895 = 0.225854

$y_{1} = a_{5} = sigmoid(0.25*0.6236336+0.35* 0.50274997 + 0.9) = \frac{1}{1+e^{1.2318708895}} = 0.225854$
节点6的输出值为

a6=sigmoid(w63a3+w64a4+w6b)a6=sigmoid(w63a3+w64a4+w6b) a 6 = s i g m o i d ( w 63 a 3 + w 64 a 4 + w 6 b ) a 6 = s i g m o i d ( w 63 a 3 + w 64 a 4 + w 6 b ) $a_{6} = sigmoid(w_{63} a_{3}+w_{64} a_{4} + w_{6b})a_{6} = sigmoid(w_{63} a_{3}+w_{64} a_{4} + w_{6b})$

y 2 = a 6 = s i g m o i d (0.35 * 0.6236336 + 0.4 * 0.50274997 + 0.9) = 1 1 + e 1.319371748 = 0.2109228

$y_{2} = a_{6} = sigmoid(0.35*0.6236336+0.4* 0.50274997 + 0.9) = \frac{1}{1+e^{1.319371748}} = 0.2109228$
可以看到和目标值的差距还比较大。
以下用数学公式进行表述：
定义网络的输入向量为：

x ⃗ = ⎡ ⎣ ⎢ x 1 x 2 1 ⎤ ⎦ ⎥ x ⃗ = ⎡ ⎣ ⎢ x 1 x 2 1 ⎤ ⎦ ⎥

$\vec{x} = \begin{bmatrix}x_{1} \\ x_{2} \\ 1 \end{bmatrix}\vec{x} = \begin{bmatrix}x_{1} \\ x_{2} \\ 1 \end{bmatrix}$
输出向量为：

y ⃗ = [y 1 y 2] y ⃗ = [y 1 y 2]

$\vec{y} = \begin{bmatrix}y_{1} \\ y_{2} \end{bmatrix}\vec{y} = \begin{bmatrix}y_{1} \\ y_{2} \end{bmatrix}$
权重矩阵为：

w 3 \to = [w 31 w 32 w 3 b]

$\vec{w_{3}} = \begin{bmatrix}w_{31} &w_{32} & w_{3b} \end{bmatrix}$

w 4 \to = [w 41 w 42 w 4 b]

$\vec{w_{4}} = \begin{bmatrix}w_{41} &w_{42} & w_{4b} \end{bmatrix}$

w 5 \to = [w 53 w 54 w 5 b]

$\vec{w_{5}} = \begin{bmatrix}w_{53} &w_{54} & w_{5b} \end{bmatrix}$

w 6 \to = [w 63 w 64 w 6 b]

$\vec{w_{6}} = \begin{bmatrix}w_{63} &w_{64} & w_{6b} \end{bmatrix}$

w ⃗ = ⎡ ⎣ ⎢ ⎢ ⎢ w 31 w 41 w 51 w 61 w 31 w 42 w 52 w 62 w 3 b w 4 b w 5 b w 6 b ⎤ ⎦ ⎥ ⎥ ⎥

$\vec{w} = \begin{bmatrix}w_{31} &w_{31} & w_{3b} \\w_{41} &w_{42} & w_{4b} \\w_{51} &w_{52} & w_{5b} \\w_{61} &w_{62} & w_{6b} \end{bmatrix}$
激活函数为：

f = s i g m o i d f = s i g m o i d

$f = sigmoidf = sigmoid$
节点的输入为：

n e t 1 = x 1

$net_{1} = x_{1}$

n e t 2 = x 2

$net_{2} = x_{2}$

n e t 3 = w 3 - \to \cdot x \to

$net_{3} = \overrightarrow{w_{3}}\cdot \overrightarrow{x}$

n e t 4 = w 4 - \to \cdot x \to

$net_{4} = \overrightarrow{w_{4}}\cdot \overrightarrow{x}$

n e t 5 = w 5 - \to \cdot ⎡ ⎣ ⎢ a 3 a 4 1 ⎤ ⎦ ⎥

$net_{5} = \overrightarrow{w_{5}}\cdot \begin{bmatrix}a_{3} \\ a_{4} \\1 \end{bmatrix}$

n e t 6 = w 6 - \to \cdot ⎡ ⎣ ⎢ a 3 a 4 1 ⎤ ⎦ ⎥

$net_{6} = \overrightarrow{w_{6}}\cdot \begin{bmatrix}a_{3} \\ a_{4} \\1 \end{bmatrix}$
节点的输出为：

a ⃗ = ⎡ ⎣ ⎢ ⎢ ⎢ a 3 a 4 a 5 a 6 ⎤ ⎦ ⎥ ⎥ ⎥

$\vec{a} = \begin{bmatrix}a_{3} \\ a_{4} \\ a_{5} \\ a_{6} \end{bmatrix}$

a 3 = f (n e t 3) = f (w 3 - \to \cdot x \to)

$a_{3} = f(net_{3}) = f(\overrightarrow{w_{3}}\cdot \overrightarrow{x})$

a 4 = f (n e t 4) = f (w 4 - \to \cdot x \to)

$a_{4} = f(net_{4}) = f(\overrightarrow{w_{4}}\cdot \overrightarrow{x})$

a 5 = y 1 = f (n e t 5)

$a_{5} =y_{1} = f(net_{5})$

a 6 = y 2 = f (n e t 6)

$a_{6} =y_{2} = f(net_{6})$
反向传播
进行反向传播前需要确定一个损失函数，损失函数有很多种，这里使用最常用的L2 loss的二分之一。

神经网络（全连接）的前向和反向传播

前向传播

悦读