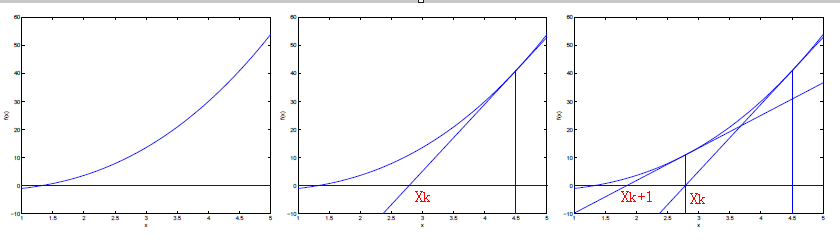
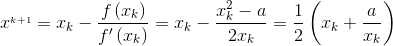问题来源:算法第四版第1.1节中有一个计算平方根的静态方法,使用的是牛顿迭代法,里面有一句 t = (c/t + t)/2.0; 这是怎么来的呢?
sqrt()方法:
public static double sqrt(double c){
if(c<0)
return Double.NaN;
double err = 1e-15;
double t = c;
while(Math.abs(t-c/t)>err*t)
t = (c/t + t)/2.0;
return t;
}
什么是牛顿迭代法:多数方程不存在求根公式,牛顿提出了一种用迭代来求方程近似根的方法。思路就是不断取切线,用线性方程的根逼近非线性方程f(x)=0的根X*。
过程简介:
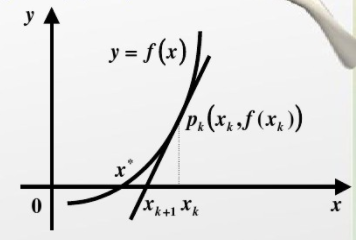

过点(Xk,f(Xk))作函数的切线,切线方程是: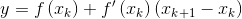
切线与x轴的交点是Xk+1,点(Xk+1,0)满足以下方程: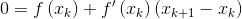
如果f'(Xk)≠0,则有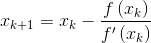
随着k的增大,Xk会不断逼近X*,即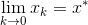
对于二次方程的求解:
求数a的平方根,其实就是求解二次方程f(x)=x^2-a=0(a>0)的正根。利用牛顿迭代公式,f'(x)=2*x,则
到这里我们就搞明白了 t = (c/t + t)/2.0 的由来。循环退出的条件是真正解与近似解的误差进入允许的范围,|X* - Xk ^2| < ε ;等价于abs(1 - c / t^2)<err,即abs(t - c / t ) < err * t 。