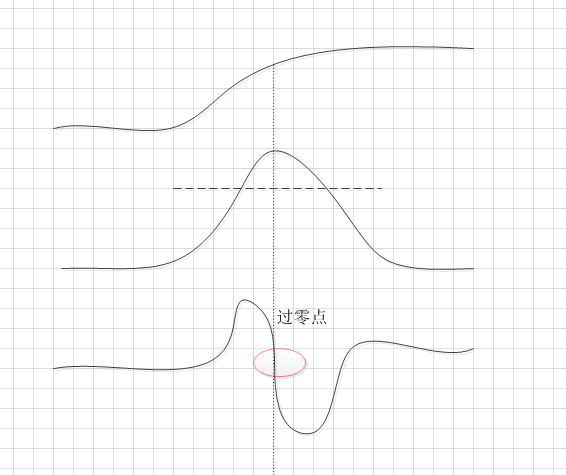
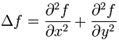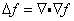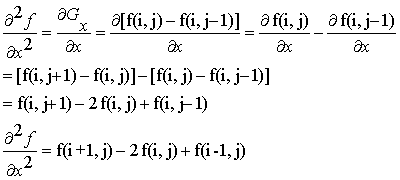如果图像灰度变化剧烈，进行一阶微分则会形成一个局部的极值，由数学上的知识，对图像进行二阶微分则会形成一个过零点，并且在零点两边产生一个波峰和波谷，我们要设定一个阈值，检测到这个过零点，如下图所示：

带来了两个好处：

1. 二阶微分关心的是图像灰度的突变而不强调灰度缓慢变化的区域，对边缘的定位能力更强。

2. Laplace算子是各项同性的，即具有旋转不变性（后面会证明），在一阶微分里，我们是用|dx|+|dy|来近似一个点的梯度的，当图像旋转一个角度时，这个值就变化了，但对于Laplace算子来说不管图像怎么旋转，得到的响应是一样的。

一个注意点：

我们检测的必须是“过零点“，而不单单是零点，也就是要保证这个被选中的点一定要是局部极值点。比如下面这个例子，上面的曲线是图像空间，虚线处的点并不是图像的局部极值点，但求二阶导的时候确实是零点。再比如图像灰度的平坦区域，不管是一阶导还是二阶导都是0，它们显然不是我们要的点：

过零点的确定：

以p为中心的一个3*3领域，p点为过零点意味着至少有两个相对的领域像素的符号不同。有四种要检测的情况：左/右、上/下，和两个对角。如果g(x,y)的值与一个阈值比较（一种通用的方法），那么不仅要求相对领域的符号不同，数值差的绝对值要超过这个阈值，这时p称为一个过零点像素。

Laplace算子

Laplace算子是梯度的散度 ：      

图像是离散的二维矩阵，用差分近似微分：

所以，