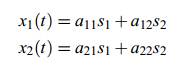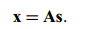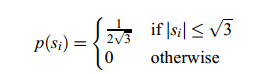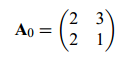1.从鸡尾酒会问题（cocktail party problem）说起

ICA最早是从神经网络领域开始研究的，应用于信号分离、特征提取。为了简单，我们这里从一个经典的例子开始——盲源信号分离（blind signal separation）。

假设在一个开party的房间里有两个人同时说话，房间里两个不同的位置上各放一个麦克风，记录了两段声音（时间信号），x1(t)和x2(t)，这两段声音都记录了两个人说的话，我们怎样得到他们分别说了什么话呢？

记源信号是s1(t)和s2(t)，这个问题可以用以下等式描述：

四个参数aij与说话者跟麦克风的距离有关。

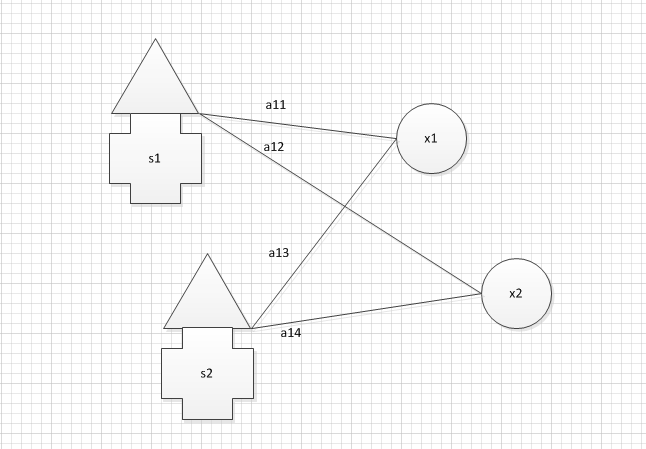
示意图如下：

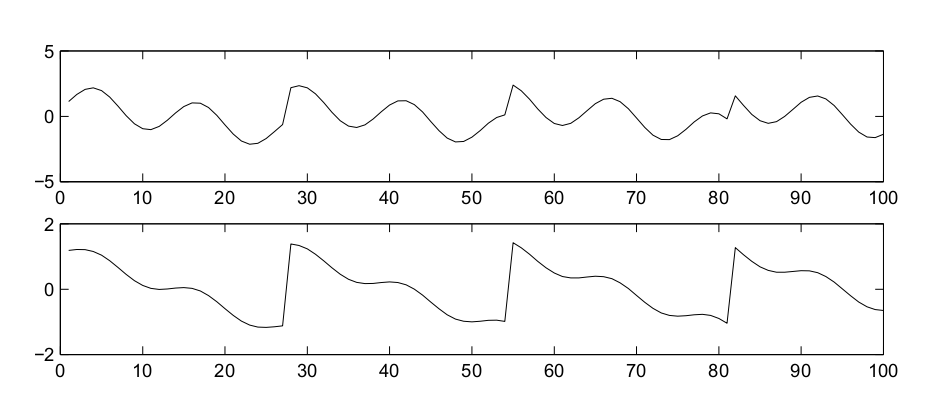
接收到的信号x1,x2:

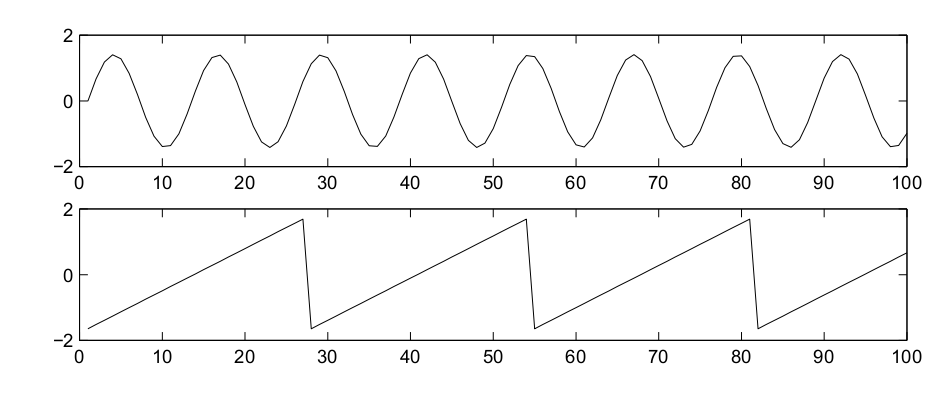
需要我们去还原的信号s1,s2：

研究表明，如果s1,s2是统计独立的随机信号，那么就可以用x1,x2去还原。ICA正是利用统计上的独立性从混合信号中分解出源信号的。

2.ICA模型介绍

2.1定义ICA

这里我们用隐含变量（latent variables）模型来描述ICA：

假设有n个观测信号x1,...,xn，来自n个独立成分的混合s1,...,sn 。其中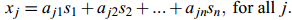A是nxn的混合矩阵（mixing matrix）。

模型假设如下：

1.si之间是统计独立的；

2.si服从非高斯分布；

3.混合矩阵是方阵（可以放松），且可逆。

那么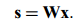，，W是A的逆。

独立成分是隐含变量，也就是说他们不能被直接观测到。A和s都是未知的。

2.2ICA的不确定性

1.不能确定独立成分的方差或者说能量

因为A和s都是未知的，s缩放的倍数可以在A上补偿回来：。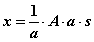

因此我们统一假设各独立分量的方差为1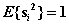，。其实，这样假设之后仍然存在一个不确定性，独立分量乘以-1并不影响方差。不过在实际应用时，并不影响。

2.不能确定各独立分量的顺序

同样，由于A和s都是未知的，在预测时我们可以任意改变A和s对应分量的位置，在矩阵运算中就是乘以一个置换矩阵：。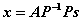

2.3举个例子

假设独立成分s1,s2服从以下均匀分布：

可以证明出这个均匀分布的均值为0，方差为1。

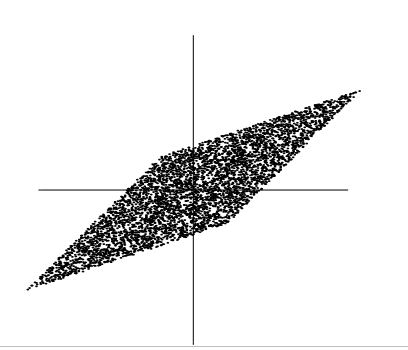
联合概率密度的分布是这样的，横轴是s1,纵轴是s2：

混合矩阵如下：

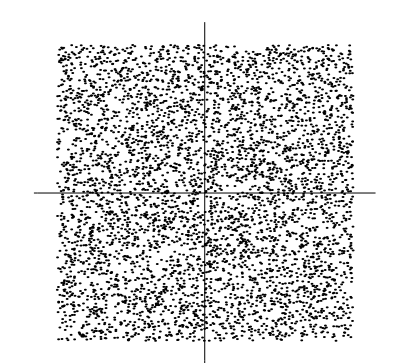
使得x1,x2在如下的平行四边形上符合均匀分布，横轴是x1,纵轴是x2：

我们要做的就是通过x1