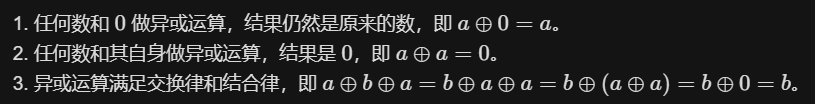目录
No.461 汉明距离
题目描述:两个整数之间的汉明距离指的是这两个数字对应二进制位不同的位置的数目。给出两个整数 x 和 y,计算它们之间的汉明距离。注意:0 ≤ x, y < 231.
解题思路:两个数字之间的汉明距离就是其二进制数对应位不同的个数,那么最直接了当的做法就是按位分别取出两个数对应位上的数并异或,我们知道异或的性质上相同的为0,不同的为1,我们只要把为1的情况累加起来就是汉明距离了。这里使用循环完成按位取出对应位上的数,对于32位的int, 多数编译器能够一次最多处理31位的左移(通过利用或运算),因此循环top设置为32。
class Solution {
public:
int hammingDistance(int x, int y) {
int res=0;
for(int i=0;i<32;i++)
{
if((x & (1<<i)) ^ (y & (1<<i)))
res++;
}
return res;
}
};No.617 合并二叉树
题目描述:给定两个二叉树,想象当你将它们中的一个覆盖到另一个上时,两个二叉树的一些节点便会重叠。你需要将他们合并为一个新的二叉树。合并的规则是如果两个节点重叠,那么将他们的值相加作为节点合并后的新值,否则不为 NULL 的节点将直接作为新二叉树的节点。
输入:
Tree 1 Tree 2
1 2
/ \ / \
3 2 1 3
/ \ \
5 4 7
输出: 合并后的树:
3
/ \
4 5
/ \ \
5 4 7
解题思路:使用递归的方法
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
TreeNode* mergeTrees(TreeNode* t1, TreeNode* t2) {
TreeNode* root=NULL;
builder(t1,t2,root);
return root;
}
void builder(TreeNode* t1,TreeNode* t2,TreeNode*& root)
{
if(!t1&&!t2) return;
if(t1&&!t2)
{
root=new TreeNode(t1->val);
builder(t1->left,NULL,root->left);
builder(t1->right,NULL,root->right);
}
else if(!t1&&t2)
{
root=new TreeNode(t2->val);
builder(NULL,t2->left,root->left);
builder(NULL,t2->right,root->right);
}
else
{
root=new TreeNode(t1->val+t2->val);
builder(t1->left,t2->left,root->left);
builder(t1->right,t2->right,root->right);
}
}
};No.226 翻转二叉树
题目描述:翻转一棵二叉树。
输入:
4
/ \
2 7
/ \ / \
1 3 6 9输出:
4
/ \
7 2
/ \ / \
9 6 3 1解题思路:使用层次遍历来完成翻转,中间借助栈来实现。
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
TreeNode* invertTree(TreeNode* root) {
//判断是否为空树
if(root==NULL)
return root;
queue<TreeNode*>Q;
Q.push(root);
while(!Q.empty())
{
TreeNode* p=Q.front();
Q.pop();
TreeNode* tmp=p->left;
p->left=p->right;
p->right=tmp;
if(p->left!=NULL)
Q.push(p->left);
if(p->right!=NULL)
Q.push(p->right);
}
return root;
}
};补充:最近看到另一个也很不错的思路,是用递归来实现翻转的。细思极恐,理解思路即可。
// Recursion
class Solution {
public:
TreeNode* invertTree(TreeNode* root) {
if (!root) return NULL;
TreeNode *tmp = root->left;
root->left = invertTree(root->right);
root->right = invertTree(tmp);
return root;
}
};No.104 二叉树的最大深度
题目描述:给定一个二叉树,找出其最大深度。二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
说明: 叶子节点是指没有子节点的节点。
解题思路:因为这个题目是考察了二叉树的深度搜索算法,深度搜索算法通常有两种解题思路,一种是递归的方法,另一种则是借助队列,通过层次遍历来统计二叉树与的深度。
解法一的代码:
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
int maxDepth(TreeNode* root) {
if(root==NULL)
return 0;
return 1+max(maxDepth(root->left),maxDepth(root->right));
}
};解决二的代码:
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
int maxDepth(TreeNode* root) {
if (!root) return 0;
int res = 0;
queue<TreeNode*> q{{root}};
while (!q.empty()) {
++res;
for (int i = q.size(); i > 0; --i) {
TreeNode *t = q.front(); q.pop();
if (t->left) q.push(t->left);
if (t->right) q.push(t->right);
}
}
return res;
}
};No.206 反转链表
题目描述:反转一个单链表。
输入: 1->2->3->4->5->NULL
输出: 5->4->3->2->1->NULL解题思路:首先,第一种思路考虑使用栈来实现,注意由栈重写链表时要注意数据的格式
class Solution {
public:
ListNode* reverseList(ListNode* head) {
stack<ListNode*>s; //定义栈结构
if(head==NULL) return head;
ListNode* p=head;
while(p!=NULL)
{
s.push(p); //入栈
p=p->next;
}
ListNode* newhead=new ListNode(0);//返回值
ListNode* q=newhead;
while(!s.empty())
{
q->next=s.top();
q=q->next;
s.pop();
}
q->next=NULL;
return newhead->next;
}
};第二种思路:对于一个有n个节点的链表而言,对n个节点进行反转,就是把第1个节点接到第2-n个节点的反转结果的末尾。那么我们只需要用递归的手法进行整个链表反转即可。注意两点:当链表为空或者只有一个节点时,直接返回头指针head;反转过后的头指针head要对其next指针置空。
class Solution {
public:
ListNode* reverseList(ListNode* head) {
if(head == NULL || head->next == NULL) return head;
ListNode* subList = reverseList(head->next), *pos = subList;
while(pos->next != NULL){
pos = pos->next;
}
head->next = NULL;
pos->next = head;
return subList;
}
};第三种思路:使用链表的头插法来构建,将第一个节点摘下来,然后依次前插入到头结点的后面,直到最后一个节点为止。时间复杂度为O(1)。这种思路目前来看应该是内存消耗最少的。
class Solution {
public:
ListNode* reverseList(ListNode* head) {
if(head==NULL) return head;
ListNode* p=head->next;
ListNode* r;
head->next=NULL;
while(p!=NULL)
{
r=p->next;
p->next=head;
head=p;
p=r;
}
return head;
}
};No.136 只出现一次的数字
题目描述:给定一个非空整数数组,除了某个元素只出现一次以外,其余每个元素均出现两次。找出那个只出现了一次的元素。说明:你的算法应该具有线性时间复杂度。 你可以不使用额外空间来实现吗?
解题思路:使用异或的方法,异或操作具有如下的性质:
class Solution {
public:
int singleNumber(vector<int>& nums) {
int res=0;
int len=nums.size();
if(len==0) return 0;
for(int i=0;i<len;i++)
{
res^=nums[i];
}
return res;
}
};No.169 多数元素
题目描述:给定一个大小为 n 的数组,找到其中的多数元素。多数元素是指在数组中出现次数大于 ⌊ n/2 ⌋ 的元素。你可以假设数组是非空的,并且给定的数组总是存在多数元素。
解题思路:使用哈希表,借助STL中的unordered_map 。
class Solution {
public:
int majorityElement(vector<int>& nums) {
unordered_map<int,int>map; //定义哈希
int max=0,flag=0;
for(int i=0;i<nums.size();i++)
{
++map[nums[i]];
if(map[nums[i]]>max)
{
flag=i;
max=map[nums[i]];
}
}
return nums[flag];
}
};No,21 合并两个有序链表
题目描述:将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。
示例:输入:1->2->4, 1->3->4 输出:1->1->2->3->4->4
解题思路:方法一,暴力法,引入哑结点,然后逐一比较两个链表取最小值。时间复杂度o(M+N)
class Solution {
public:
ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {
ListNode* l3=new ListNode(-1);
ListNode* p=l3;
while(l1!=nullptr&&l2!=nullptr)
{
if(l1->val>l2->val)
{
p->next=l2;
l2=l2->next;
}
else if(l1->val<=l2->val)
{
p->next=l1;
l1=l1->next;
}
p=p->next;
}
while(l1!=nullptr)
{
p->next=l1;
l1=l1->next;
p=p->next;
}
while(l2!=nullptr)
{
p->next=l2;
l2=l2->next;
p=p->next;
}
p->next=nullptr;
return l3->next;
}
};方法二:使用递归的思路,递归公式定义如下:
class Solution {
public:
ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {
if(l1==nullptr)
return l2;
else if(l2==nullptr)
return l1;
else if(l1->val<l2->val)
{
l1->next=mergeTwoLists(l1->next,l2);
return l1;
}
else
{
l2->next=mergeTwoLists(l1,l2->next);
return l2;
}
}
};No.539 把二叉搜索树转换为累加树
题目描述:给定一个二叉搜索树(Binary Search Tree),把它转换成为累加树(Greater Tree),使得每个节点的值是原来的节点值加上所有大于它的节点值之和。
例如:
输入: 原始二叉搜索树:
5
/ \
2 13
输出: 转换为累加树:
18
/ \
20 13
解题思路:使用中序遍历的思想,可以看到,5->18是加了右子树的值,而2->20是加了根与右子树的值,因此可以构建递归函数实现累加树。
class Solution {
public:
TreeNode* convertBST(TreeNode* root) {
int sum=0;
getGreater(root,sum);
return root;
}
void getGreater(TreeNode* bt,int& sum)
{
if(bt==NULL)
return;
getGreater(bt->right,sum);
bt->val+=sum;
sum=bt->val;
getGreater(bt->left,sum);
}
};No.283 移动零
题目描述:给定一个数组 nums,编写一个函数将所有 0 移动到数组的末尾,同时保持非零元素的相对顺序。
解题思路:使用快慢指针,快指针负责遍历非0元,然后与慢指针指向的值交换。
class Solution {
public:
void moveZeroes(vector<int>& nums) {
for(int i=0,j=0;i<nums.size();i++)
{
if(nums[i])
swap(nums[i],nums[j++]);
}
}
};No.448 找到所有数组中
题目描述:给定一个范围在 1 ≤ a[i] ≤ n ( n = 数组大小 ) 的 整型数组,数组中的元素一些出现了两次,另一些只出现一次。
找到所有在 [1, n] 范围之间没有出现在数组中的数字。您能在不使用额外空间且时间复杂度为O(n)的情况下完成这个任务吗? 你可以假定返回的数组不算在额外空间内。
解题思路:这类问题的一个重要条件就是1 ≤ a[i] ≤ n (n = size of array),不然很难在O(1)空间和O(n)时间内完成。对于每个数字nums[i],如果其对应的nums[nums[i] - 1]是正数,我们就赋值为其相反数,如果已经是负数了,就不变了,那么最后我们只要把留下的整数对应的位置加入结果res中即可
class Solution {
public:
vector<int> findDisappearedNumbers(vector<int>& nums) {
vector<int> res;
for (int i = 0; i < nums.size(); ++i) {
int idx = abs(nums[i]) - 1;
nums[idx] = (nums[idx] > 0) ? -nums[idx] : nums[idx];
}
for (int i = 0; i < nums.size(); ++i) {
if (nums[i] > 0) {
res.push_back(i + 1);
}
}
return res;
}
};No.160 相交链表
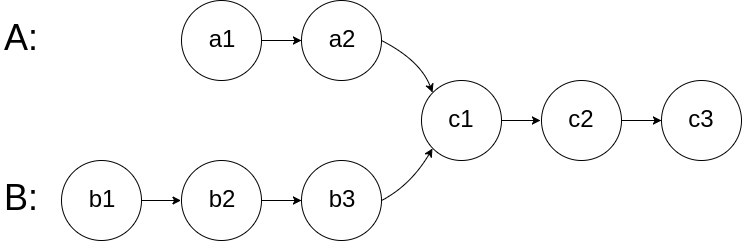
题目描述:编写一个程序,找到两个单链表相交的起始节点。如下面的两个链表:在节点 c1 开始相交。
示例 1:
输入:intersectVal = 8, listA = [4,1,8,4,5], listB = [5,0,1,8,4,5], skipA = 2, skipB = 3
输出:Reference of the node with value = 8
输入解释:相交节点的值为 8 (注意,如果两个链表相交则不能为 0)。从各自的表头开始算起,链表 A 为 [4,1,8,4,5],链表 B 为 [5,0,1,8,4,5]。在 A 中,相交节点前有 2 个节点;在 B 中,相交节点前有 3 个节点。
解题思路:先同步遍历两个链表,求两者长度的差值,然后第二次先遍历差值长度,再接着共同遍历,直至两者相交,return。
class Solution {
public:
ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
if(headA==NULL||headB==NULL) return NULL;
int len1=GetLength(headA),len2=GetLength(headB);
if(len1<len2)
for(int i=0;i<len2-len1;i++)
headB=headB->next;
if(len1>len2)
for(int i=0;i<len1-len2;i++)
headA=headA->next;
while(headA&&headB&&headB!=headA)
{
headA=headA->next;
headB=headB->next;
}
return (headA&&headB) ? headA:NULL;
}
int GetLength(ListNode* head)
{
if(head==NULL) return 0;
int len=0;
while(head!=NULL)
{
head=head->next;
len++;
}
return len;
}
};No.155 最小栈
题目描述:设计一个支持 push ,pop ,top 操作,并能在常数时间内检索到最小元素的栈。
push(x) —— 将元素 x 推入栈中。
pop() —— 删除栈顶的元素。
top() —— 获取栈顶元素。
getMin() —— 检索栈中的最小元素。
解题思路:用空间换时间,定义一个辅助栈,辅助栈每次保存栈顶元素都是最小值
class MinStack {
public:
stack<int>s; //当前栈
stack<int>tmp;//保存最小元素的栈
/** initialize your data structure here. */
MinStack() {
tmp.push(INT_MAX); //保持最小元素的栈,栈顶元素永远是最小值
}
void push(int x) {
s.push(x);
tmp.push(min(tmp.top(),x)); //能插入的始终都是最小的
}
void pop() {
s.pop(); //出栈
tmp.pop();
}
int top() {
return s.top();
}
int getMin() {
return tmp.top();
}
};No.1 两数之和
题目描述:给定一个整数数组 nums 和一个目标值 target,请你在该数组中找出和为目标值的那 两个 整数,并返回他们的数组下标。你可以假设每种输入只会对应一个答案。但是,数组中同一个元素不能使用两遍。
示例:
给定 nums = [2, 7, 11, 15], target = 9
因为 nums[0] + nums[1] = 2 + 7 = 9
所以返回 [0, 1]
解题思路:题目本身不难,关键就是要想清楚题目中的逻辑
class Solution:
def twoSum(self, nums: List[int], target: int) -> List[int]:
hash={}
for i in range(0,len(nums)):
hash[nums[i]]=i
for j in range(0,len(nums)):
if target-nums[j] in hash.keys() and j!=hash[target-nums[j]]:
return [j,hash[target-nums[j]]]No.5 最长回文子串
题目描述:给定一个字符串 s,找到 s 中最长的回文子串。你可以假设 s 的最大长度为 1000。
示例 1:
输入: "babad"
输出: "bab"
注意: "aba" 也是一个有效答案。
解题思路:使用滑动窗口的思想
class Solution {
public:
string longestPalindrome(string s) {
int left,right;
int start=0,maxlen=0;
for(int i=0;i<s.size();i++)
{
find(s,i,i,start,maxlen); //奇数个字符
find(s,i,i+1,start,maxlen); //偶数个字符
}
return s.substr(start,maxlen);
}
void find(string s,int left,int right,int &start,int &maxlen)
{
while(left>=0&&right<s.size()&&s[left]==s[right])
{
left--;
right++;
}
if(maxlen<right-left-1)
{
start=left+1;
maxlen=right-left-1;
}
}
};No.15 三数之和
题目描述:给你一个包含 n 个整数的数组 nums,判断 nums 中是否存在三个元素 a,b,c ,使得 a + b + c = 0 ?请你找出所有满足条件且不重复的三元组。
注意:答案中不可以包含重复的三元组。
解题思路:首先需要对数组进行排序,排完之后先检查合理性,即数组中是否全部是正数或者全部是负数。在确认完后,设定target表示另外两数的和,然后使用二分查找法进行查找。
class Solution {
public:
vector<vector<int>> threeSum(vector<int>& nums) {
vector<vector<int>>res;
sort(nums.begin(),nums.end()); //先排序
if(nums.empty()||nums.back()<0||nums.front()>0)
return {};
for(int i=0;i<(int)nums.size()-2;i++)
{
if(nums[i]>0) break;
if(i>0 && nums[i]==nums[i-1]) continue; //保持不重复
int target=0-nums[i],left=i+1,right=nums.size()-1;
while(left<right)
{
if(nums[left]+nums[right]==target)
{
res.push_back({nums[i],nums[left],nums[right]});
while(left<right&&nums[left]==nums[left+1]) left++;
while(left<right&&nums[right]==nums[right-1]) right--;
left++;
right--;
}
else if(nums[left]+nums[right]<target) left++;
else right--;
}
}
return res;
}
};No.3 无重复字符的最长子串
题目描述:给定一个字符串,请你找出其中不含有重复字符的 最长子串 的长度。
示例 1:
输入: "abcabcbb"
输出: 3
解释: 因为无重复字符的最长子串是 "abc",所以其长度为 3。
解题思路:使用哈希表作为数据结构,每次记录不重复的字符串的index
class Solution {
public:
int lengthOfLongestSubstring(string s) {
unordered_map<int,int>hash;
int res=0,left=-1,n=s.size();
for(int i=0;i<n;i++)
{
//如果有重复的
if(hash.count(s[i])&&hash[s[i]]>left)
{
left=hash[s[i]];
}
hash[s[i]]=i; //记录索引数
res=max(res,i-left); //记录当前最大长度
}
return res;
}
};No.696 计数二进制子串
题目描述:给定一个字符串 s,计算具有相同数量0和1的非空(连续)子字符串的数量,并且这些子字符串中的所有0和所有1都是组合在一起的。重复出现的子串要计算它们出现的次数。
示例 1 :
输入: "00110011"
输出: 6
解释: 有6个子串具有相同数量的连续1和0:“0011”,“01”,“1100”,“10”,“0011” 和 “01”。
请注意,一些重复出现的子串要计算它们出现的次数。另外,“00110011”不是有效的子串,因为所有的0(和1)没有组合在一起。
示例 2 :
输入: "10101"
输出: 4
解释: 有4个子串:“10”,“01”,“10”,“01”,它们具有相同数量的连续1和0。
解题思路:直接用pre和cur两个变量,其中pre初始化为0,cur初始化为1,然后从第二个数字开始遍历,如果当前数字和前面的数字相同,则cur自增1,否则pre赋值为cur,cur重置1。然后判断如果pre大于等于cur,res自增1。其实核心思想跟上面的方法一样,只不过pre和cur可以在0和1之间切换
class Solution {
public:
int countBinarySubstrings(string s) {
int res=0,pre=0,cur=1;
for(int i=1;i<s.size();i++)
{
if(s[i]==s[i-1]) cur++;
else
{
pre=cur;
cur=1;
}
if(pre>=cur) res++;
}
return res;
}
};No.4 寻找两个正序数组的中位数
题目描述:给定两个大小为 m 和 n 的正序(从小到大)数组 nums1 和 nums2。请你找出这两个正序数组的中位数,并且要求算法的时间复杂度为 O(log(m + n))。你可以假设 nums1 和 nums2 不会同时为空。
解题思路:二分查找方法,两个指针分别指向两个数组,同步比较,每次挪动k-1步,直至遍历得到结果。
class Solution {
public:
int getres(vector<int>nums1,vector<int>nums2,int k)
{
int index1=0,index2=0;
int m=nums1.size(),n=nums2.size();
while(true)
{
//边界情况
if(index1==m)
return nums2[index2+k-1];
if(index2==n)
return nums1[index1+k-1];
if(k==1)
return min(nums1[index1],nums2[index2]);
//正常情况
int newIndex_index1=min(index1+k/2-1,m-1);
int newIndex_index2=min(index2+k/2-1,n-1);
if(nums1[newIndex_index1]<=nums2[newIndex_index2])
{
k-=newIndex_index1-index1+1;
index1=newIndex_index1+1;
}
else
{
k-=newIndex_index2-index2+1;
index2=newIndex_index2+1;
}
}
}
double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {
int totalLength = nums1.size() + nums2.size();
if (totalLength % 2 == 1) {
return getres(nums1, nums2, (totalLength + 1) / 2);
}
else {
return (getres(nums1, nums2, totalLength / 2) + getres(nums1, nums2, totalLength / 2 + 1)) / 2.0;
}
}
};No.3 无重复字符的最长子串
题目描述:给定一个字符串,请你找出其中不含有重复字符的 最长子串 的长度。
解题思路:使用滑动窗口,每次都遍历后面数字没在set中的,插入,算出所有可能值的最大值
class Solution:
def lengthOfLongestSubstring(self, s: str) -> int:
res=set()
right,ans=-1,0
for i in range(len(s)):
if i!=0:
res.remove(s[i-1])
while right+1!=len(s) and s[right+1] not in res:
res.add(s[right+1])
right+=1
ans=max(ans,right-i+1)
return ansNo.85 最大矩阵
题目描述:给定一个仅包含 0 和 1 的二维二进制矩阵,找出只包含 1 的最大矩形,并返回其面积。
示例:
输入:
[
["1","0","1","0","0"],
["1","0","1","1","1"],
["1","1","1","1","1"],
["1","0","0","1","0"]
]
输出: 6
解题思路:使用辅助数组逐行遍历,记录每行累积“1”的个数,取每一行最小的1的个数做为宽,逐行统计面积
class Solution:
def maximalRectangle(self, matrix: List[List[str]]) -> int:
max_area=0
dp=[[0]*len(matrix[0]) for _ in range(len(matrix))]
for i in range(len(matrix)):
for j in range(len(matrix[0])):
if matrix[i][j]=='0': continue
width=dp[i][j]=dp[i][j-1]+1 if j else 1
for k in range(i,-1,-1):
width=min(width,dp[k][j])
max_area=max(max_area,width*(i-k+1))
return max_area