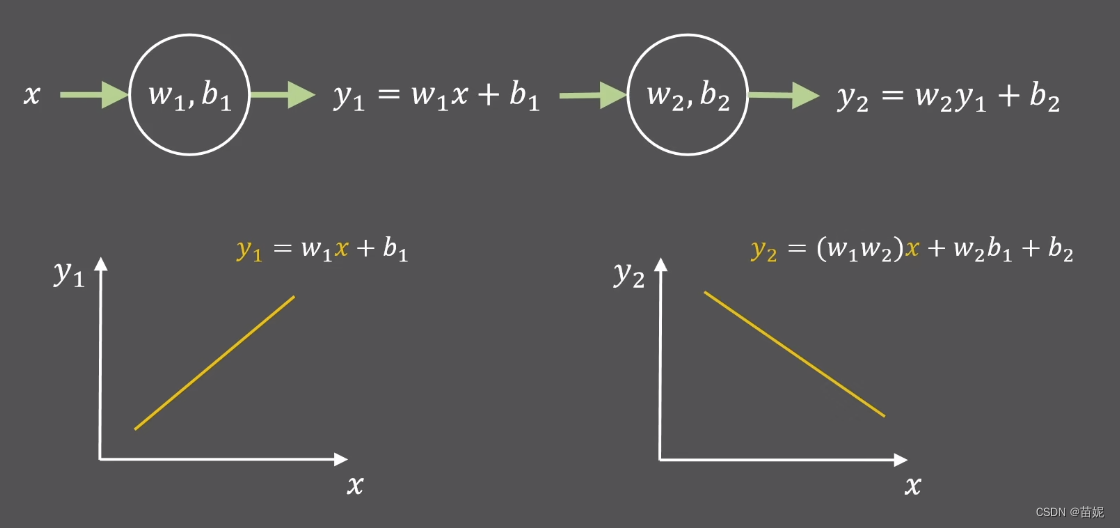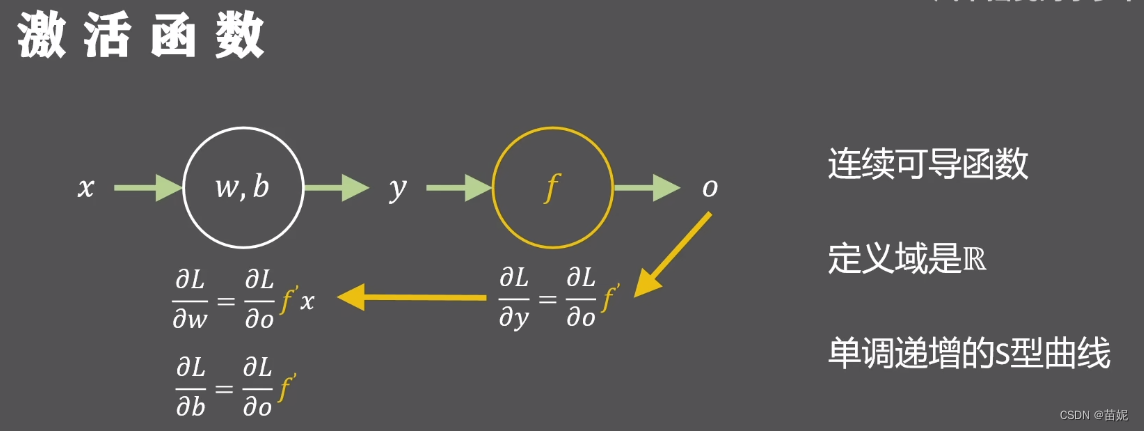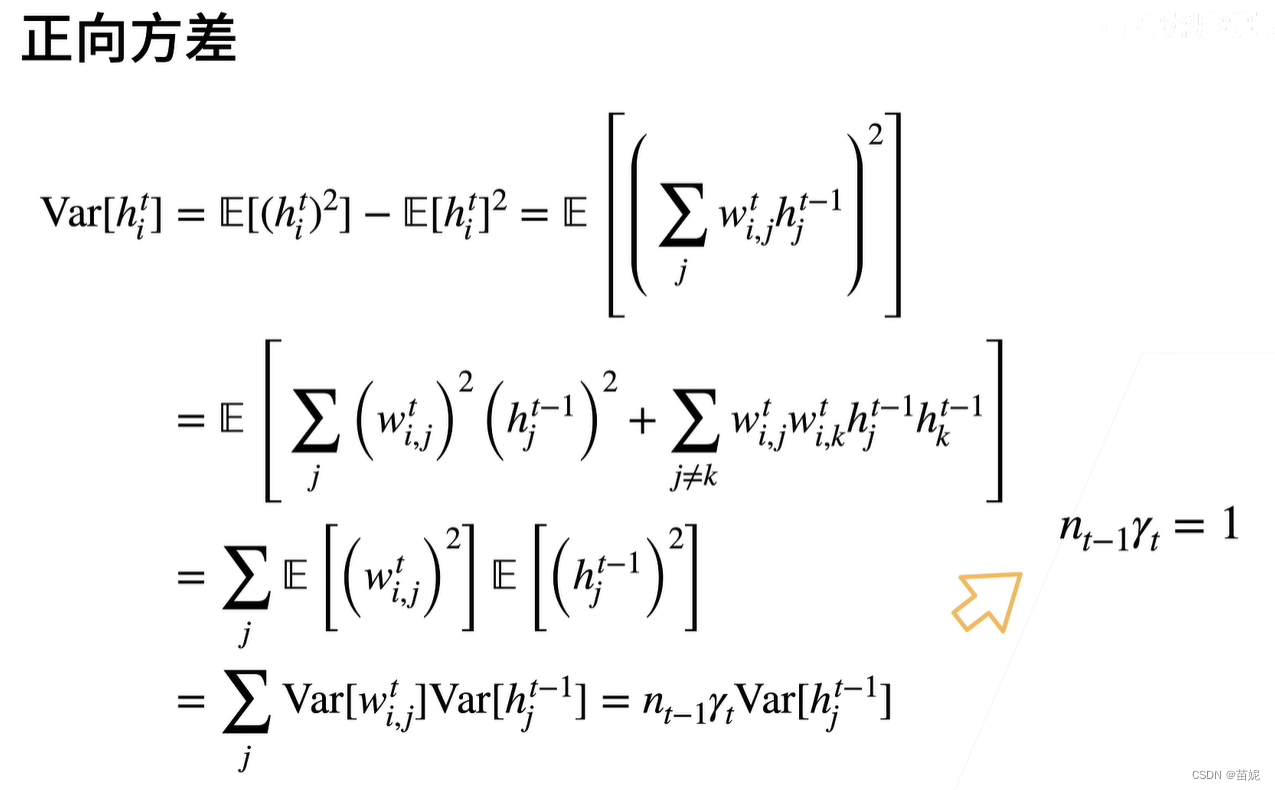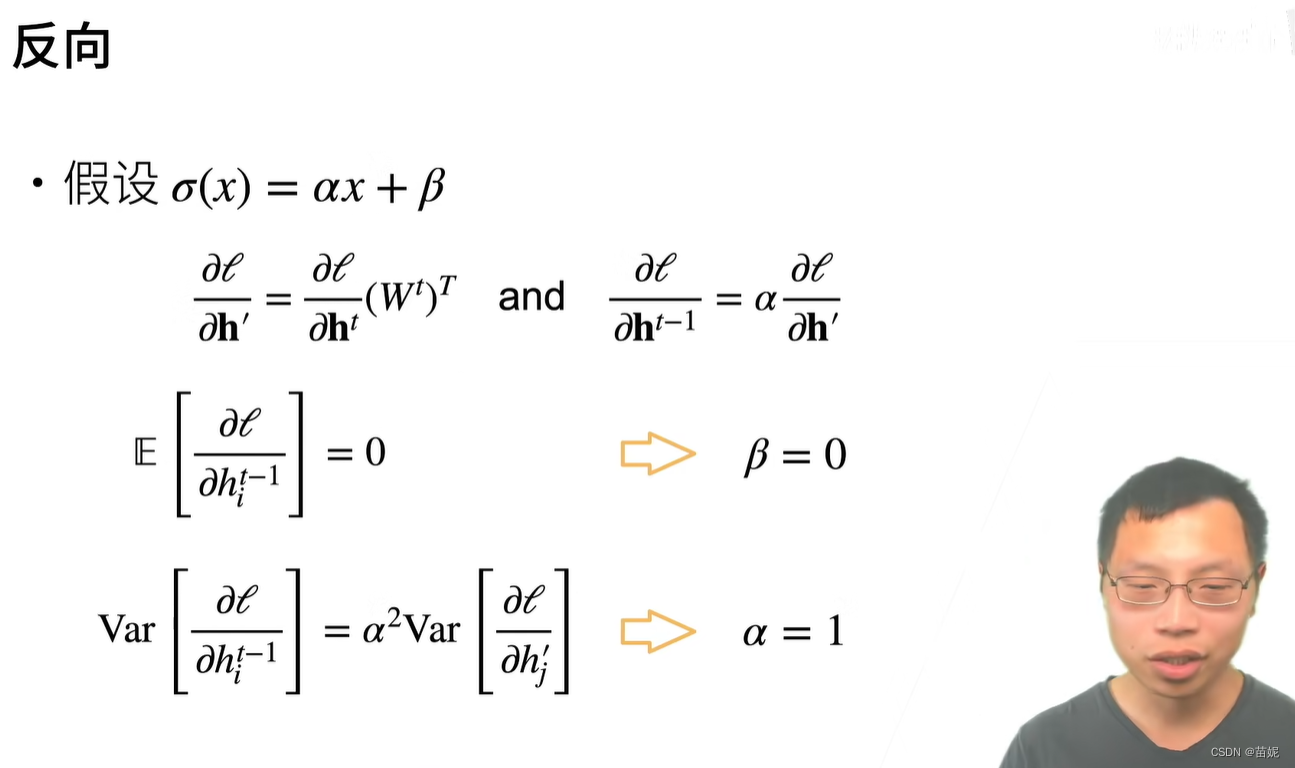1、为什么要在深度网络中引入激活函数？
激活函数的引入为神经网络提供了非线性变换的能力。没有激活函数，即使神经网络有多个层次，其输出仍然是输入的线性组合，这将限制其表达复杂函数的能力。通过使用非线性激活函数，神经网络能够学习和表示更复杂的任务和模式。
2、激活函数需要具备什么特点？
1、非线性 （增加网络的非线性表达能力）
2、激活函数
f
f
f 需要连续可导 （满足反向传播链式求导）
3、定义域是R (满足不同输入的要求)
4、单调递增 （保证相对输入大小不变）
3、梯度消失和梯度爆炸
考虑一个具有
L
L
L 层、输入
x
\mathbf{x}
x 和输出
o
\mathbf{o}
o 的深层网络。 每一层
l
l
l 由变换
f
l
f_l
fl 定义， 该变换的参数为权重
W
(
l
)
\mathbf{W}^{(l)}
W(l)， 其隐藏变量是
h
(
l
)
\mathbf{h}^{(l)}
h(l)（令
h
(
0
)
=
x
\mathbf{h}^{(0)} = \mathbf{x}
h(0)=x）。 我们的网络可以表示为：
h
(
l
)
=
f
l
(
h
(
l
−
1
)
)
因此
o
=
f
L
∘
…
∘
f
1
(
x
)
.
(
1
)
\mathbf{h}^{(l)} = f_l (\mathbf{h}^{(l-1)}) \text{ 因此 } \mathbf{o} = f_L \circ \ldots \circ f_1(\mathbf{x}). (1)
h(l)=fl(h(l−1)) 因此 o=fL∘…∘f1(x).(1)
如果所有隐藏变量和输入都是向量， 我们可以将
o
\mathbf{o}
o 关于任何一组参数
W
(
l
)
\mathbf{W}^{(l)}
W(l) 的梯度写为下式：
∂
W
(
l
)
o
=
∂
h
(
L
−
1
)
h
(
L
)
⏟
M
(
L
)
=
d
e
f
⋅
…
⋅
∂
h
(
l
)
h
(
l
+
1
)
⏟
M
(
l
+
1
)
=
d
e
f
⏟
L
−
l
次矩阵乘法
∂
W
(
l
)
h
(
l
)
⏟
v
(
l
)
=
d
e
f
.
(
2
)
\partial_{\mathbf{W}^{(l)}} \mathbf{o} = \underbrace{\underbrace{\partial_{\mathbf{h}^{(L-1)}} \mathbf{h}^{(L)}}_{ \mathbf{M}^{(L)} \stackrel{\mathrm{def}}{=}} \cdot \ldots \cdot \underbrace{\partial_{\mathbf{h}^{(l)}} \mathbf{h}^{(l+1)}}_{ \mathbf{M}^{(l+1)} \stackrel{\mathrm{def}}{=}} }_{L-l 次矩阵乘法}\underbrace{\partial_{\mathbf{W}^{(l)}} \mathbf{h}^{(l)}}_{ \mathbf{v}^{(l)} \stackrel{\mathrm{def}}{=}}. (2)
∂W(l)o=L−l次矩阵乘法
M(L)=def
∂h(L−1)h(L)⋅…⋅M(l+1)=def
∂h(l)h(l+1)v(l)=def
∂W(l)h(l).(2)
换言之，该梯度是
L
−
l
L-l
L−l个矩阵
M
(
L
)
⋅
…
⋅
M
(
l
+
1
)
\mathbf{M}^{(L)} \cdot \ldots \cdot \mathbf{M}^{(l+1)}
M(L)⋅…⋅M(l+1) 与梯度向量
v
(
l
)
\mathbf{v}^{(l)}
v(l)的乘积。当网络很深，
L
−
l
L-l
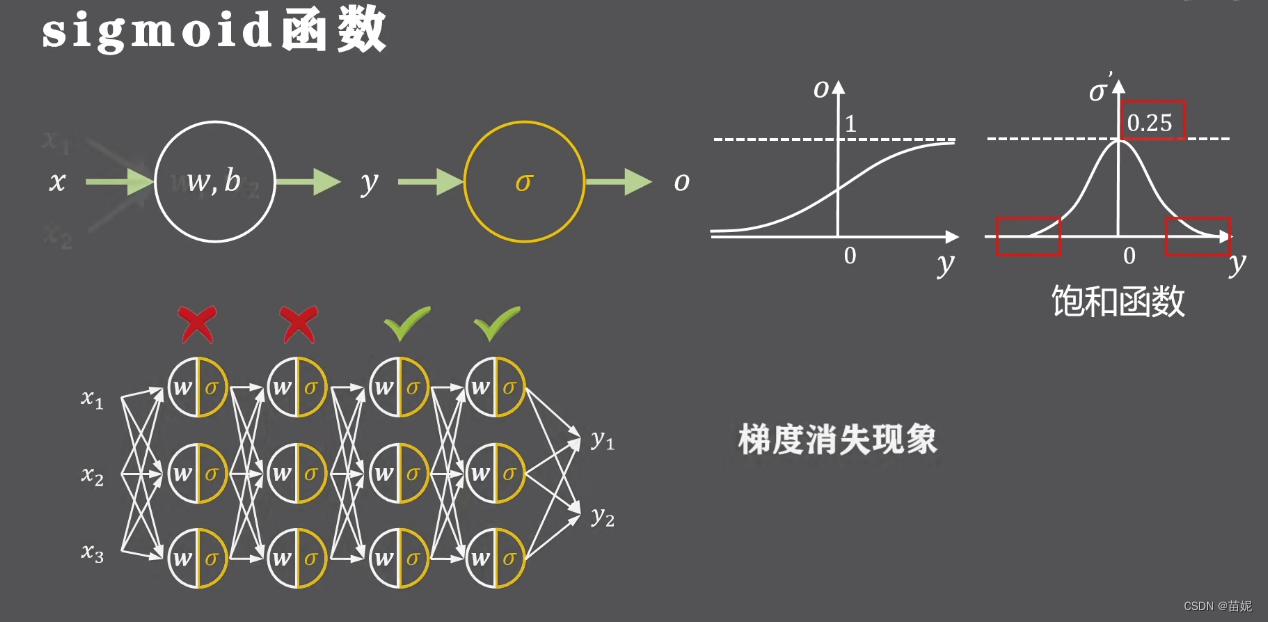
L−l足够大时； 即使每层的值在1附近，他们的乘积可能非常大，也可能非常小，即导致梯度爆炸或梯度消失。如下图所示。
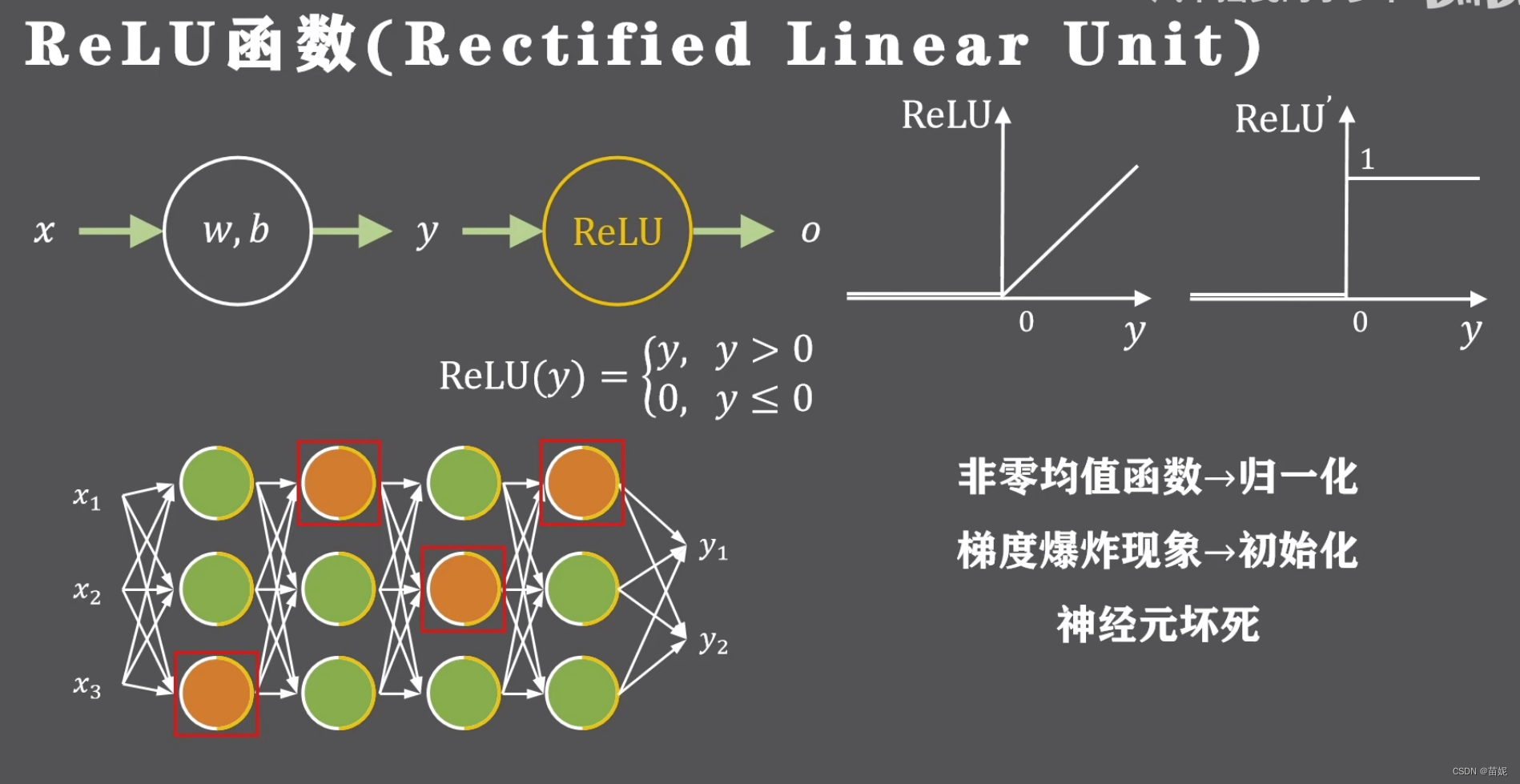
梯度爆炸（Gradient Explosion）：
当在反向传播过程中，梯度的值变得非常大，甚至超过计算机能够表示的范围时，就会发生梯度爆炸。这会导致权重更新过大，网络参数变得不稳定，甚至无法收敛到合理的解决方案。
梯度消失（Gradient Vanishing）：
在反向传播过程中，梯度的值变得非常小，甚至趋近于零。这会导致靠近输入端的网络参数几乎无法更新，仅更新靠近输出端的网络参数，即使设计的网络很深，但实际上仅获得浅层网络的设计效果（仅输出端附近有效）。
4、激活函数分类
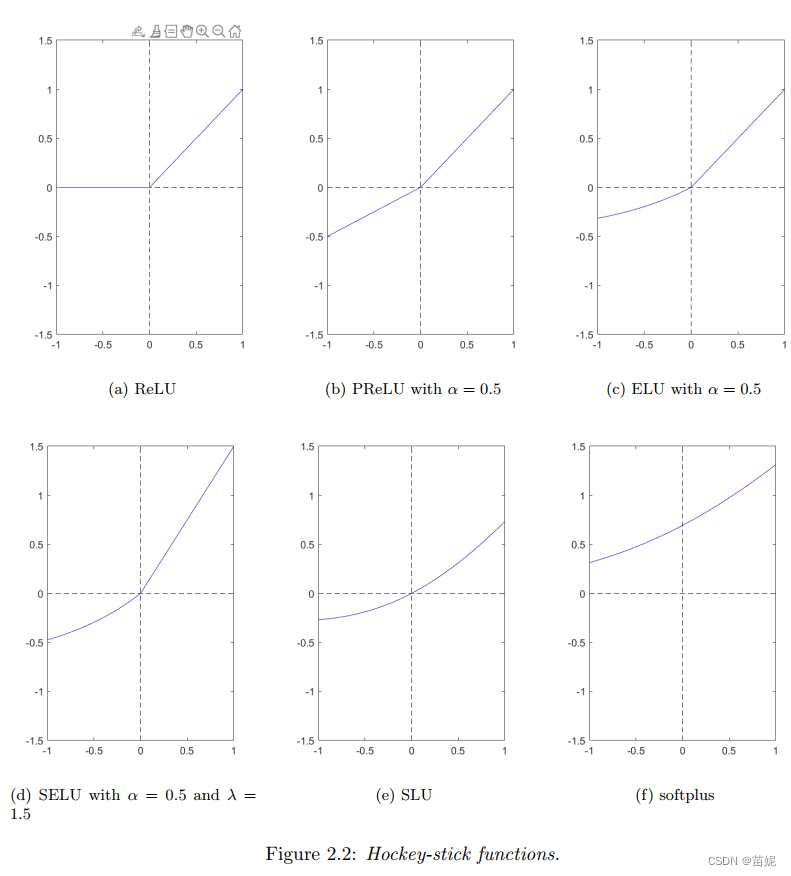
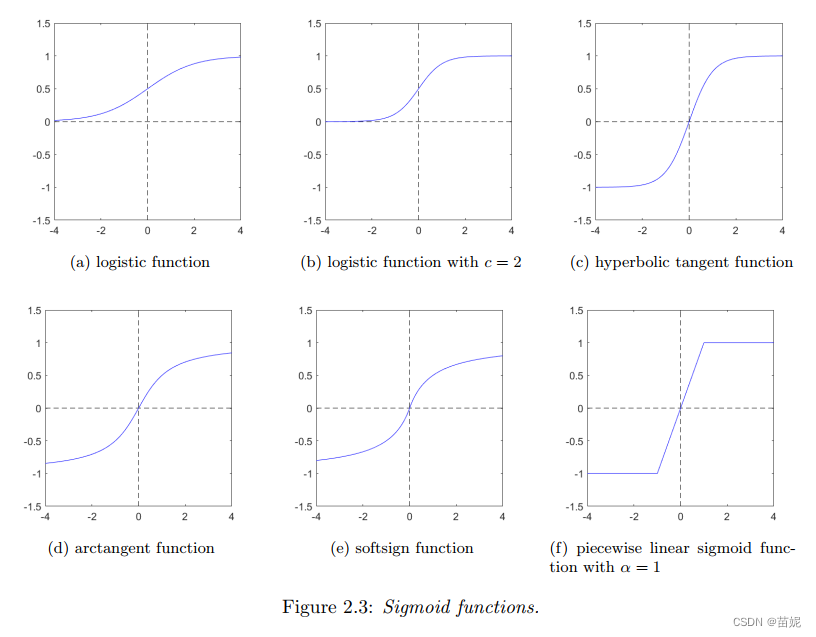
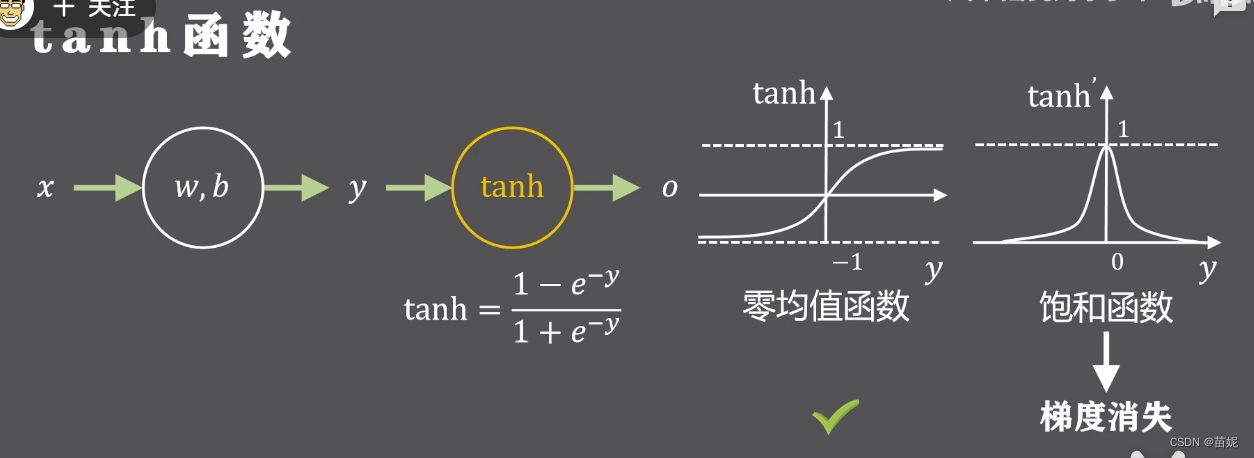
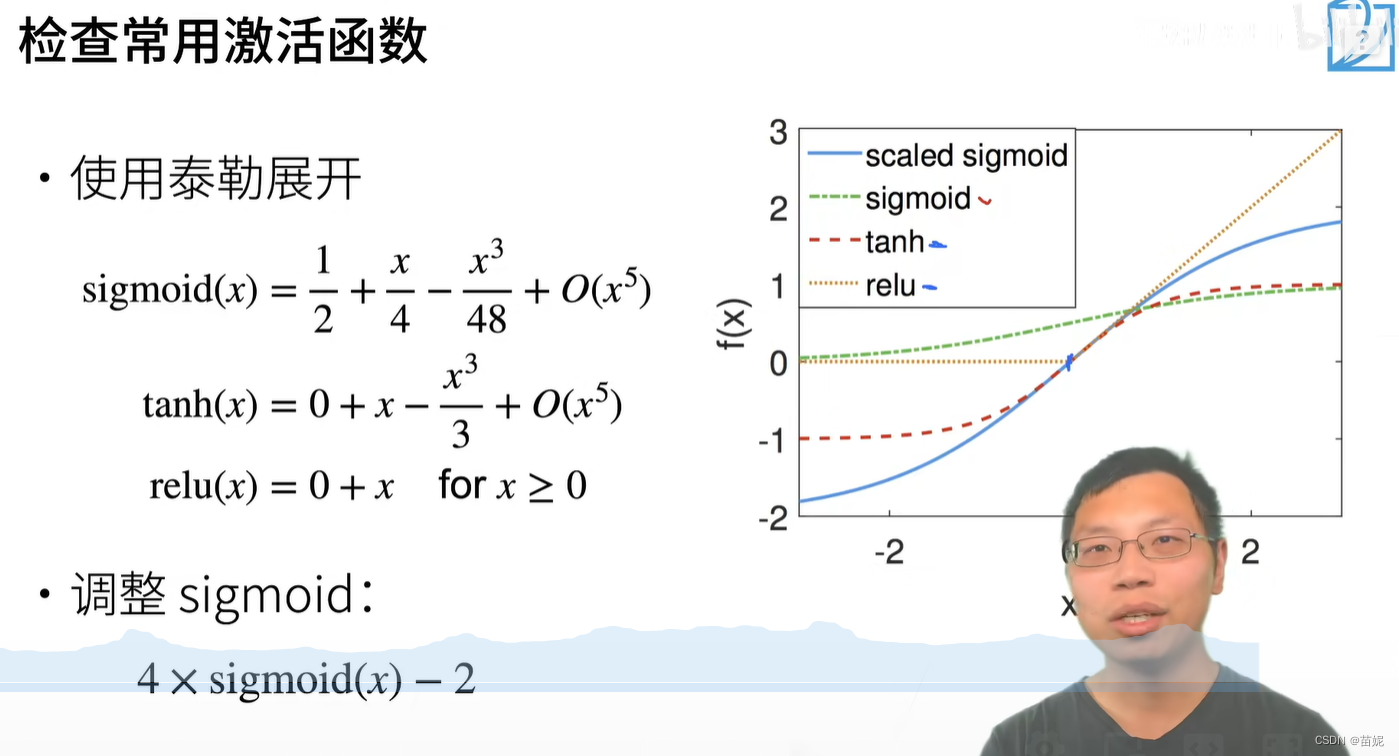
主要有两类激活函数，分别为：ReLU family， Sigmoid family
5、举例： sigmoid 系列
好的激活函数，应该尽量避免梯度消失和梯度爆炸，将导致训练不稳定的因素降到最低。
即需要：
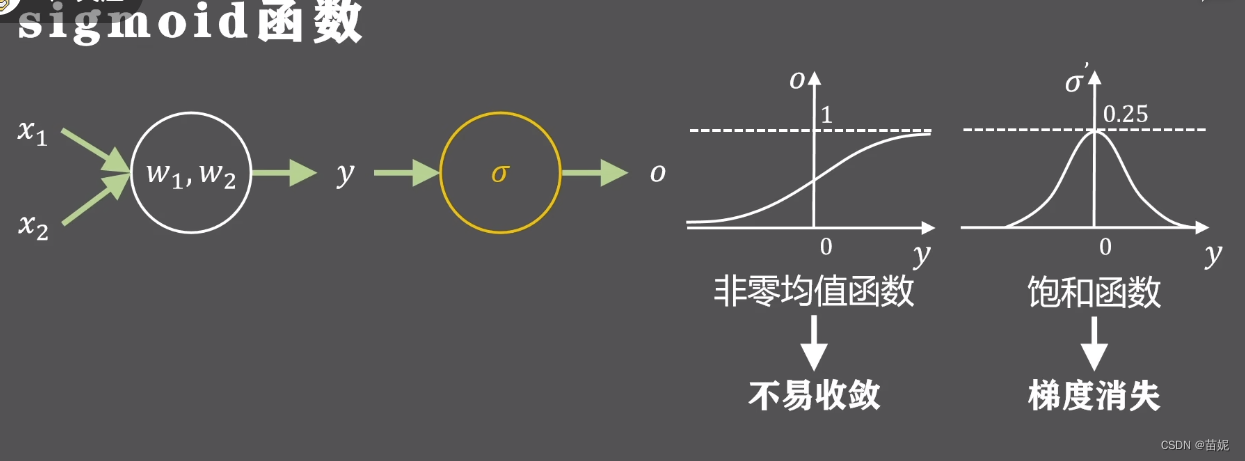
1）激活函数的导数为非饱和函数，避免梯度消失
2）激活函数为零均值函数，促进训练过程收敛
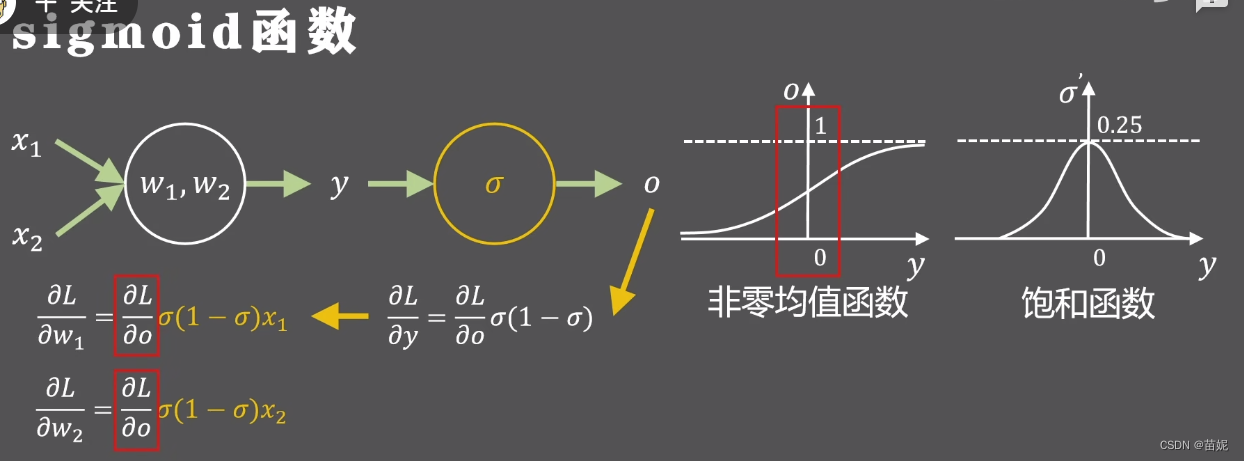
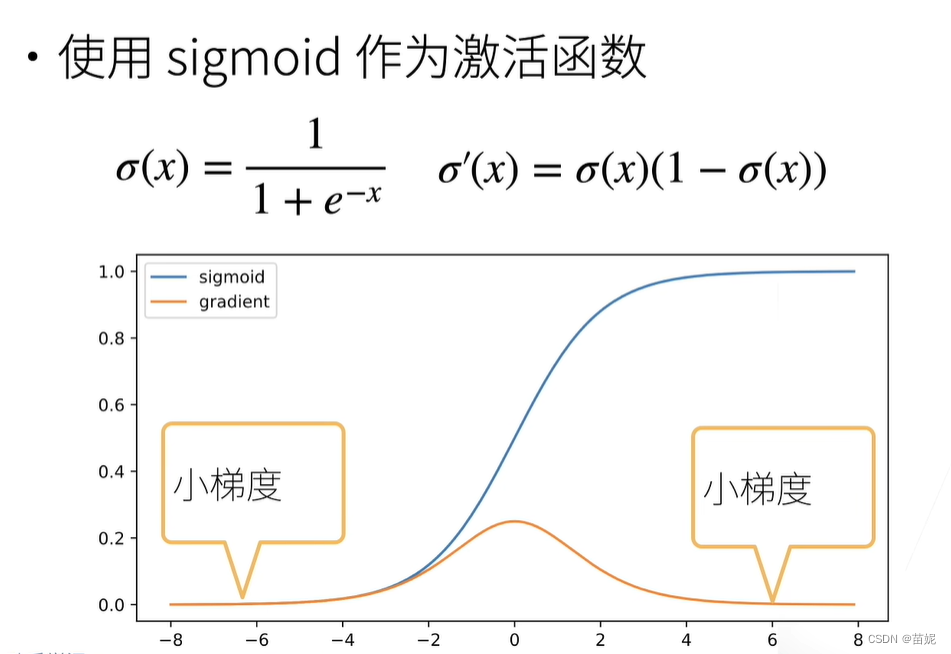
经过分析，我们发现sigmoid函数不具有以上两个性质。
σ
(
x
)
=
1
1
+
e
−
x
\sigma(x) = \frac{1}{1+e^{-x}}
σ(x)=1+e−x1
图中对
w
1
w_1
w1 和
w
2
w_2
w2分别求导，黄色式子始终为正，对这两个参数求导，正负完全取决于损失函数对输出的导数，即同时为正或者同时为负数，被强制的同时正向或者反向更新，这种情况会使得神经网络更慢的收敛到预定位置。
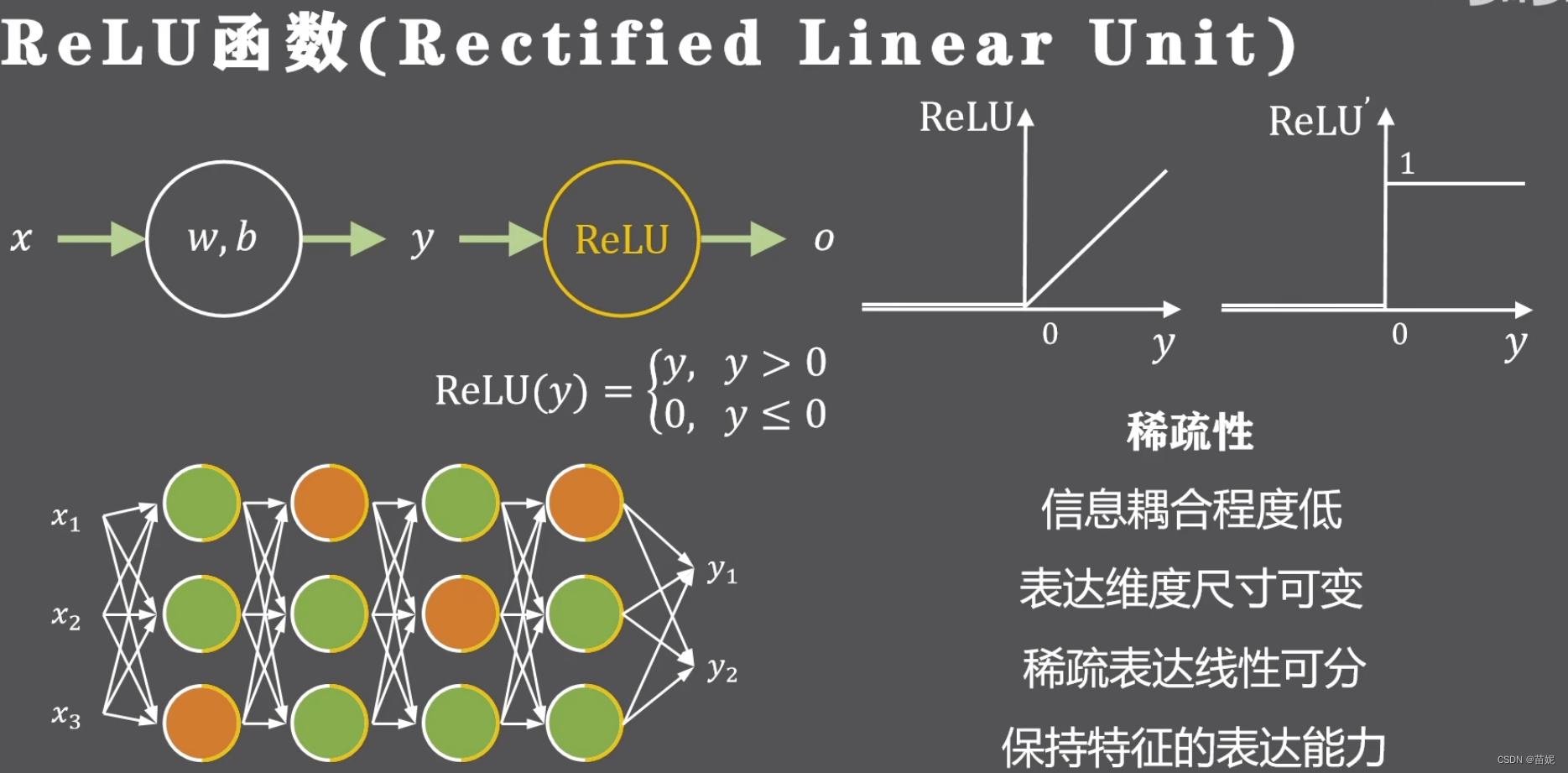
6、 举例：ReLU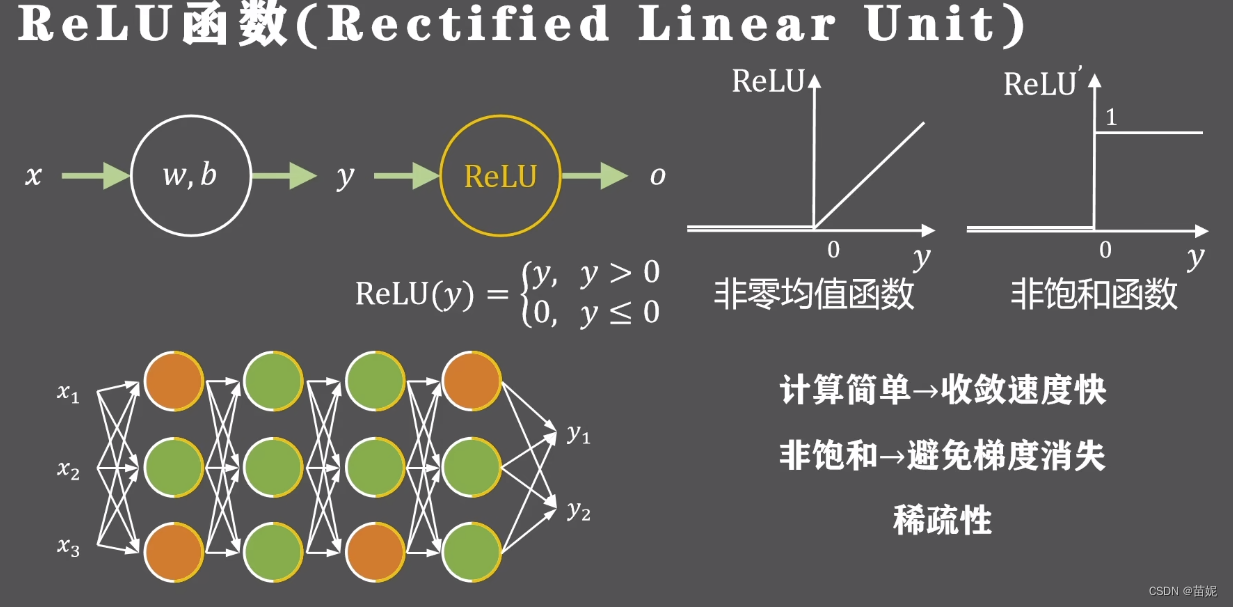
如果输入的参数发生了很小的改动，那么只有小部分神经元需要改变状态，而不需要全局调整，使得信息耦合程度降低；
动态开启和关闭神经元的做法可以支持不同输入维度和中间层维度的特征学习；
稀疏表达的方式一般是线性可分或弱线性可分，降低网络训练的难度；
虽然输出的特征是稀疏的，但被激活的输出任然保持原有的表达能力；
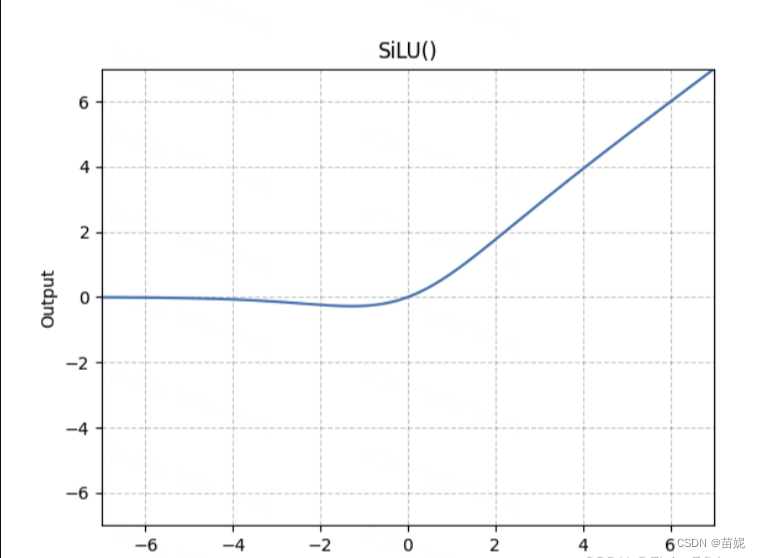
7、举例：Sigmoid 和 ReLU的组合版 ------> SiLU
SiLU 函数是一种神经网络中的激活函数，全称是 Sigmoid Gated Linear Unit（Sigmoid门控线性单元）, 也被称为 Swish 函数。它由 Google Brain 在 2017 年提出，是一种非线性激活函数，能够有效地对神经网络的输入进行非线性变换。
定义:
f ( x ) = x ∗ σ ( x ) f(x) = x * \sigma (x) f(x)=x∗σ(x)
其中： σ ( x ) = 1 1 + e − x \sigma(x) = \frac{1}{1+e^{-x}} σ(x)=1+e−x1
SiLU 函数的特点如下：
正数区域内，SiLU 函数的输出与 ReLU 函数的输出相同。
在负数区域内，SiLU 函数的输出与 sigmoid 函数的输出相同。
SiLU 函数在整个定义域内都是可微的，这使得在反向传播过程中的梯度计算更加稳定。
SiLU函数不是单调递增的，而是在x≈−1.28时达到全局最小值−0.28，这可以起到一个隐式正则化的作用，抑制过大的权重
3、选择激活函数的标准？
训练过程稳定->数值稳定->避免梯度消失和梯度爆炸
5、激活函数与反向求导
以多层感知机为例，此处为了简单省略了偏移。
h
(
l
)
=
f
l
(
h
(
l
−
1
)
)
=
σ
(
W
(
l
)
h
(
l
−
1
)
)
(
3
)
\mathbf{h}^{(l)} = f_l(\mathbf{h}^{(l - 1)}) = \sigma (\mathbf{W}^{(l)}\mathbf{h}^{(l-1)}) \text (3)
h(l)=fl(h(l−1))=σ(W(l)h(l−1))(3)
∂
h
(
l
)
∂
h
(
l
−
1
)
=
f
l
(
h
(
l
−
1
)
)
=
d
i
a
g
(
σ
′
(
W
(
l
)
h
(
l
−
1
)
)
)
(
W
(
l
)
)
T
(
4
)
\frac{\partial\mathbf{h}^{(l)}}{\partial\mathbf{h}^{(l-1)}} = f_l(\mathbf{h}^{(l - 1)}) =diag(\sigma^{\prime}(\mathbf{W}^{(l)}\mathbf{h}^{(l-1)})) (\mathbf{W}^{(l)}) ^T \text (4)
∂h(l−1)∂h(l)=fl(h(l−1))=diag(σ′(W(l)h(l−1)))(W(l))T(4)
∏
i
=
l
L
−
1
∂
h
(
i
+
1
)
∂
h
(
i
)
=
∏
i
=
l
L
−
1
d
i
a
g
(
σ
′
(
W
(
i
)
h
(
i
−
1
)
)
)
(
W
(
i
)
)
T
(
5
)
\prod_{i=l}^{L-1}\frac{\partial\mathbf{h}^{(i+1)}}{\partial\mathbf{h}^{(i)}} =\prod_{i=l}^{L-1}diag(\sigma^{\prime}(\mathbf{W}^{(i)}\mathbf{h}^{(i-1)})) (\mathbf{W}^{(i)}) ^T \text (5)
i=l∏L−1∂h(i)∂h(i+1)=i=l∏L−1diag(σ′(W(i)h(i−1)))(W(i))T(5)
6、梯度爆炸
1）举例
2）梯度爆炸问题
7、梯度消失
1）举例
2）梯度消失问题
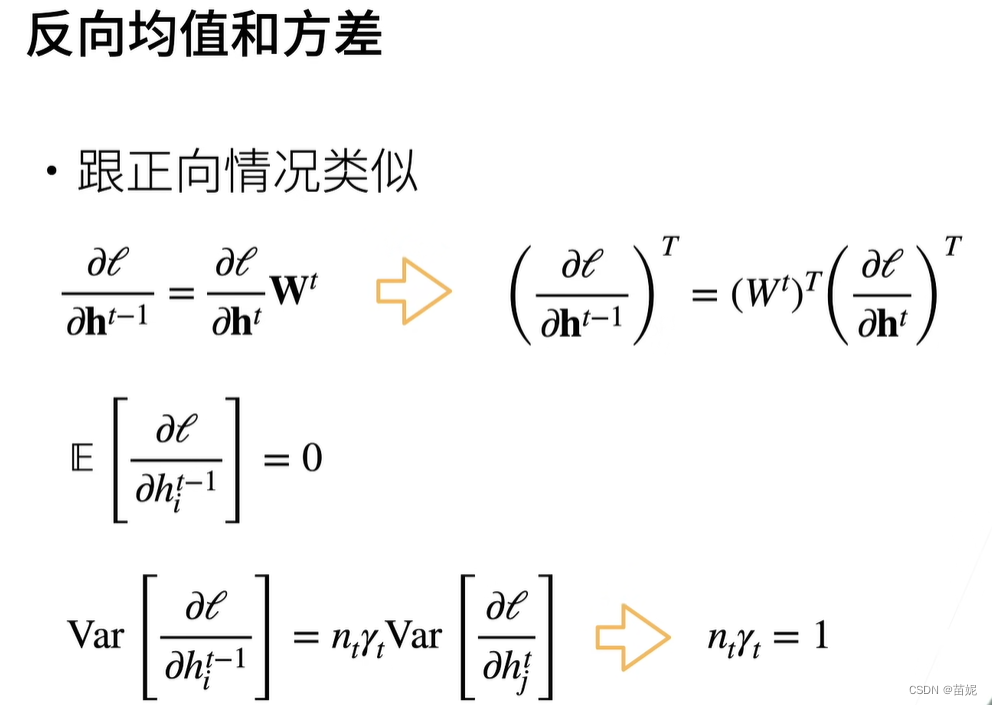
8、权重初始化
在输出和梯度满足随机分布的情况下，如何做权重初始化。
9、激活函数选择
合理的权重初始化（每层的输出和每层的梯度都是均值为0方差为固定数的随机变量）
