SVG之Path
目录
一、Path概述
1、控制命令
2、格式
3、简单的演示编辑器
二、移动和直线命令
三、弧线命令
四、贝塞尔曲线命令
1、贝塞尔曲线概述
2、二次贝塞尔曲线命令:Q
3、三次贝塞尔曲线命令:C
4、光滑贝塞尔曲线
5、知识回顾与拓展思考
一、Path概述
1、控制命令
SVG提供了一些基础图形元素标签如<circle>、<rect>、<ellipse>、<line>、<polyline>等,但是如果我们想要绘制一些特别的形状,比如一些曲线,那么我们就需要使用<path>标签,即路径标签。如果你足够熟练<path>,你可以使用它绘制任何图形!
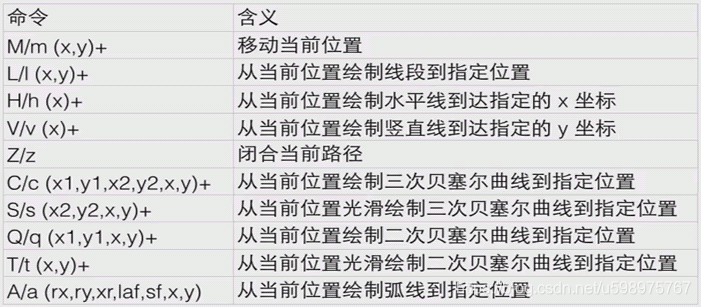
<path>标签提供了一些路径控制命令,如下:
2、格式
3、简单的演示编辑器
下面是一个简单的path演示器,我们可以输入控制命令来动态生成路径:
-
1 <!DOCTYPE html> 2 <html> 3 <head> 4 <meta charset="utf-8"> 5 <title>path直线演示</title> 6 <style> 7 html, body { 8 margin: 0; 9 padding: 0; 10 } 11 #svg { 12 display: block; 13 width: 100%; 14 height: 100%; 15 } 16 textarea { 17 display: block; 18 position: absolute; 19 bottom: 0; 20 left: 0; 21 width: 98%; 22 height: 80px; 23 border: 0; 24 border-top: 2px solid gray; 25 font-size: 30px; 26 outline: none; 27 padding: 0 1%; 28 margin: 0; 29 font-size: 30px; 30 } 31 </style> 32 </head> 33 <body> 34 <!--控件--> 35 <textarea id="pathString" placeholder="输入path命令"></textarea> 36 <svg xmlns="http://www.w3.org/2000/svg" width="1400" height="600"> 37 <path id="path" fill="none" stroke="red" stroke-width="2"></path> 38 </svg> 39 </body> 40 <script type="text/javascript"> 41 //oninput事件:当用户进行表单输入时触发 42 pathString.oninput = function(){ 43 document.getElementById('path').setAttribute('d',pathString.value); 44 }; 45 </script> 46 </html>
二、移动和直线命令
我们使用上面的编辑器来演示一下:
三、弧线命令
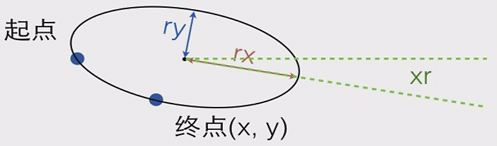
SVG的弧线使用A(rx,ry.xr,laf,sf,x,y)命令来完成,原理是通过截取一个椭圆的弧线而得到想要的弧线,
那么我们首先要构造一个椭圆:使用rx,ry,xr三个参数来构造这个椭圆,rx是椭圆的x半轴长,ry是y半轴长,xr是是弧线所在椭圆的长轴角度。
其次,我们发现这样构造出来的椭圆其实有两种,而起点到终点的弧线有四种,所以我们需要使用laf、sf、x、y四个参数来选择想要的弧线。laf表示是否选择较长弧,sf表示是否选择逆时针方向那条弧。
我们同样使用编辑器来感受一下:
四、贝塞尔曲线命令
1、贝塞尔曲线概述
上面我们说到A命令可以绘制弧线,但是很多时候还是难以画出想要的效果,所以我们常常使用贝塞尔工具进行二维绘图。我们要使用好这个绘图工具,我们就需要明白其中的原理。
贝塞尔曲线由法国数学家Pierre Bézier发明。贝塞尔曲线就是这样的一条曲线,它是依据四个位置任意的点坐标绘制出的一条光滑曲线。在历史上,研究贝塞尔曲线的人最初是按照已知曲线参数方程来确定四个点的思路设计出这种矢量曲线绘制法。贝塞尔曲线的有趣之处更在于它的“皮筋效应”,也就是说,随着点有规律地移动,曲线将产生皮筋伸引一样的变换,带来视觉上的冲击。1962年,法国数学家Pierre Bézier第一个研究了这种矢量绘制曲线的方法,并给出了详细的计算公式,因此按照这样的公式绘制出来的曲线就用他的姓氏来命名是为贝塞尔曲线。
百科:贝塞尔曲线是计算机图形图像造型的基本工具,是图形造型运用得最多的基本线条之一。它通过控制曲线上的四个点(起始点、终止点以及两个相互分离的中间点)来创造、编辑图形。其中起重要作用的是位于曲线中央的控制线。这条线是虚拟的,中间与贝塞尔曲线交叉,两端是控制端点。移动两端的端点时贝塞尔曲线改变曲线的曲率(弯曲的程度);移动中间点(也就是移动虚拟的控制线)时,贝塞尔曲线在起始点和终止点锁定的情况下做均匀移动。注意,贝塞尔曲线上的所有控制点、节点均可编辑。这种“智能化”的矢量线条为艺术家提供了一种理想的图形编辑与创造的工具。
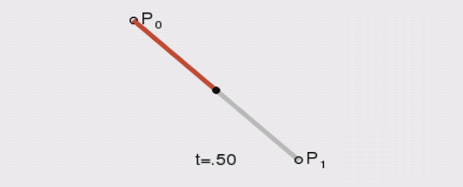
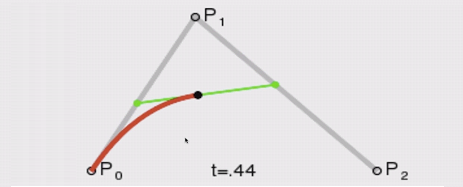
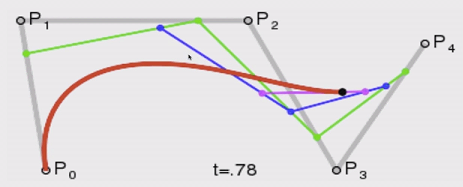
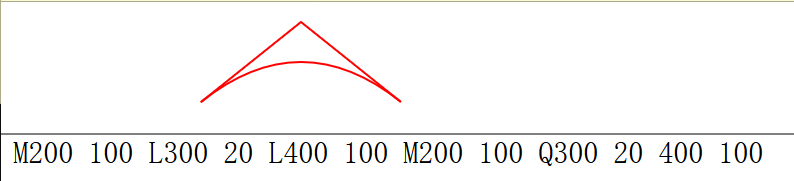
也许很多点我们一时间很难理解,我们现在的目标是认识贝塞尔曲线的大体描述,然后慢慢在实践运用中理解其中含义。下面是4种中间点不存在、存在一个中间点、存在两个中间点、存在三个中间点的情况,我们能够绘制二次贝塞尔曲线和三次贝塞尔曲线,即图2和图3:
2、二次贝塞尔曲线命令:Q
两次贝塞尔曲线有一个中间点,quadratic是两次的,二次方程式的意思,所以使用Q命令来进行二次贝塞尔曲线绘制。利用编辑器:
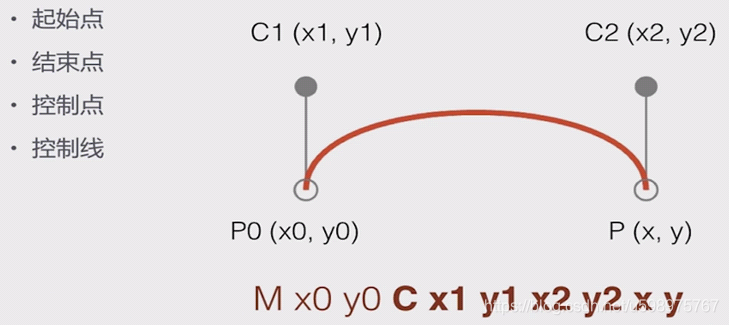
3、三次贝塞尔曲线命令:C
三次贝塞尔曲线有两个中间点三条线段,cubic是三次的,立方的的意思,所以使用C命令来绘制三次贝塞尔曲线。利用编辑器:
4、光滑贝塞尔曲线
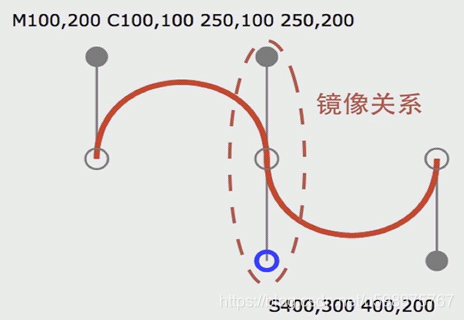
这里说的光滑曲线其实是镜像曲线,比如下面这个三次曲线,如果我们需要绘制一条镜像对称的光滑曲线,我们应该使用C250,300 400,300 400,200来进行绘制,为了方便书写,我们省略镜像对称点(图中的蓝色点),进而用S命令来表示即可:S400,300 400,200。
简单理解就是S命令和T命令省略了上一次曲线最后一个控制点关于终点镜像对称的下一次曲线第一个控制点的书写。(图中的蓝点不用作为参数写出来)。
如果需要模拟更多的贝塞尔曲线,可自行搜索或参考:
http://cubic-bezier.com/#.17,.67,.83,.67
http://myst729.github.io/bezier-curve/
5、知识回顾与拓展思考