时间序列是在时间点上形成的数值序列,时间序列预测是通过观察历史数据预测未来的值。ARIMA模型(Autoregressive Integrated Moving Average model)是时间序列预测分析方法之一,全称叫做自回归差分移动*均模型。
本文是看网上博客整理而来,原始文章是:
一,模型的构成
ARIMA模型包含3个部分,即自回归(AR)、差分(I)和移动*均(MA),它们的含义分别是:
- AR表示自回归(Auto Regression),
- I 表示单整阶数(Integration),时间序列必须是*稳的,才能建立计量模型。对时间序列进行单位根检验,如果是非*稳序列,那么需要通过差分转化为*稳序列,经过几次差分转化为*稳序列,就称为几阶单整;
- MA表示移动*均模型(Moving Average)
ARIMA模型记作ARIMA(p,d,q),p为自回归项数;q为滑动*均项数,d为使之成为*稳序列所做的差分次数(阶数)。“差分”是关键步骤,采用ARIMA模型预测的时序数据,必须是稳定的(*稳性),不稳定的数据,是无法捕捉到时序规律的。
ARIMA模型实际上是AR模型和MA模型的组合,ARIMA模型与ARMA模型的区别:ARMA模型是针对*稳时间序列建立的模型,而ARIMA模型是针对非*稳时间序列建立的模型。换句话说,非*稳时间序列要建立ARMA模型,首先需要经过差分转化为*稳时间序列,然后建立ARMA模型。
- 模型的优点是:模型简单,只需要内生变量而不需要借助其他外生变量。
- 模型的缺点是:要求时序数据是稳定的,或者通过差分化之后是稳定的;本质上只能捕捉线性关系,不能捕捉非线性关系。
1,AR模型
描述当前值与历史值之间的关系,用变量自身的历史时间数据对自身进行预测,自回归模型必须满足*稳性的要求
一般情况下,p阶自回归过程的公式定义:
yt是当前值,u是常数项,P是阶数,ri是自相关系数,et是误差,即 白噪声。
公式展开:
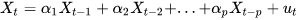
如果随机扰动项是一个白噪声(
![[公式]](/image/aHR0cHM6Ly9pLWJsb2cuY3NkbmltZy5jbi9ibG9nX21pZ3JhdGUvNjA5YWIyMDgyNDRhYzA1NTgwNzlmOTUyYzA2YmM1ZWQucG5n) ),即 u=0, 则称AR模型为一个纯AR(p)过程,记为:
),即 u=0, 则称AR模型为一个纯AR(p)过程,记为: