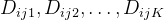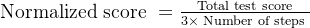机器人领域中的scaling law：通过复现斯坦福机器人UMI——探讨数据规模化定律(含UMI的复现关键)

前言

在24年10.26/10.27两天，我司七月在线举办的七月大模型机器人线下营时，我们带着大家一步步复现UMI，比如把杯子摆到杯盘上(其中1-2位学员朋友还亲自自身成功做到该任务)

此外，我还特地邀请了针对UMI做了改进工作的fastumi作者之一丁老师给大家在线分享，毕竟UMI本身有不少局限性，比如耦合性太强、原装硬件的成本太高(比如UR5e、WSG50夹爪)且不方便换成国产硬件、复杂的SLAM算法

所以才有对于UMI的局限性

丁老师那边侧重不断推进umi的改进：fastumi「详见此文：Fast-UMI——改进斯坦福UMI的硬件：用RealSense T265替代SLAM且实现机械臂的迁移与平替」，他们也将在11月上旬开源软件代码
当然，我司七月后续也会尝试下fastumi，预计12月中旬左右完成
我司七月则先侧重推进dexcap，预计11月份内完成
至于原装umi效果的提升(调参数、采集数据集训练模型、标定坐标关系)，则在做dexcap或者fastumi过程中，如来得及则顺便把这点做了，否则则和后续的某波b端层面的原装umi效果提升需求一块做

且在和丁老师沟通中，还聊到清华高阳团队也复现了UMI，不过他们是完全用的国外比较昂贵的硬件(Franka机械臂、WSG50夹爪)，且即便如此，竟然也没达到UMI原始论文中的效果，至于原论文中的效果不好达到的原因，则众说纷纭了..

而高阳团队的复现UMI的工作对应的论文为《Data Scaling Laws in Imitation Learning for Robotic Manipulation》，当然，他们这篇论文主要是为了探讨机器人领域的数据缩放定律，只是刚好用的UMI而已，但考虑到其对「我司UMI的改进及机器人训练数据收集工作」有一定的参考和启发性，故本文解读下该篇论文

第一部分清华高阳团队提出：机器人领域中的scaling law

1.1 数据缩放定律实验的前置准备工作

1.1.1 数据缩放定律的制定、数据来源

现有最大的数据库Open X-Embodiment（OXE）（Padalkar等人，2023）包含来自22种机器人化身的超过100万条机器人轨迹。OXE扩展的主要目标是开发一个基础的机器人模型，以促进不同机器人之间的正迁移学习

然而，在新环境中部署此类模型仍需进行数据收集以进行微调。相比之下，清华高阳团队的扩展目标是训练一种策略，可以直接在新环境和未知对象中部署，消除微调的需求

在泛化维度上，他们使用行为克隆（BC）来训练单任务策略。然而，许多通过BC训练的策略表现出较差的泛化性能。这种泛化问题在两个维度上表现出来

环境——泛化到以前未见过的环境，这可能涉及光照条件的变化、干扰物体、背景变化等
物体——泛化到与人类演示中同类的新物体，这些物体在颜色、大小、几何形状等属性上有所不同

故，对于环境变化，他们通过在各种自然环境中收集人类演示来扩大真实场景的数量；对于对象变化，他们通过获取大量同类日常物品来扩大可访问对象的数量

为简单起见，他们考虑一个场景

其中一个操控任务的演示数据集是在个环境 $E_{1}, E_{2}, \ldots, E_{M}$ 和个同类操控对象 $O_{1}, O_{2}, \ldots, O_{N}$ 中收集的
每个环境可以包含任意数量的干扰对象，只要它们与操控对象不属于同一类别
在一个环境中，对每个对象收集K个演示 $D_{i j 1}, D_{i j 2}, \ldots, D_{i j K}$

他们使用测试分数S在训练中未见过的环境和对象上评估策略的性能。本文中的数据缩放定律旨在：

描述和变量, , 和之间的关系，特别是泛化能力如何依赖于环境、对象和演示的数量
以及根据这种关系，确定实现所需泛化水平的有效数据收集策略

在数据来源上，我们选择使用通用操作接口UMI来收集数据，毕竟其作为手持夹具，可以比较方便且独立的收集大量演示数据，当然了，由于UMI依赖于SLAM来捕获末端执行器的动作，在纹理缺乏的环境中可能会遇到挑战

1.1.2 策略学习、验证评估

在策略学习上

他们采用扩散策略来建模我们收集的大量数据，且使用基于CNN的U-Net(Ronneberger等，2015)作为噪声预测网络，并采用DDIM(Song等，2020a)来减少推理延迟，实现实时控制

且为了进一步提高性能，他们还做了两项改进

DINOv2视觉编码器：在他们的实验中，对DINOv2 ViT(Oquab等，2023)的微调表现优于ImageNet预训练的ResNet(He等，2016；Deng等，2009)和CLIP ViT(Radford等，2021)

他们将这一改进归因于DINOv2特征能够显式捕捉图像中的场景布局和物体边界（Caron等，2021）。这些信息对于增强空间推理至关重要，这对机器人控制尤其有利（Hu等，2023b；Yang等，2023；Kim等，2024）。为了确保模型容量在数据扩展时不成为瓶颈，我们使用了足够大的模型，ViT-Large/14（Dosovitskiy等，2020）
时间集成：扩散策略每 $T_{1}$ 步预测一个动作序列，每个序列的长度为（），且仅执行前步

且他们观察到，执行的动作序列之间的不连续性会在切换时导致动作抖动。为了解决这个问题，他们实施了ACT 提出的时间集成策略

具体来说，策略在每个时间步进行预测，导致动作序列重叠。在任意给定的时间步，多重预测的动作使用指数加权方案进行平均，平滑过渡并减少动作不连续性

在效果的验证评估上，他们进行严格的评估以确保结果的可靠性

首先，为了评估策略的泛化性能，专门在未见过的环境或未见过的物体上进行测试
其次，使用测试人员分配的分数作为主要评估指标。每个操作任务分为若干阶段或步骤（通常为 2-3 个），每个阶段有明确的评分标准（见附录 D），每个步骤最多可获得 3 分

然后报告归一化分数，定义为
$\text { Normalized score }=\frac{\text { Total test score }}{3 \times \text { Number of steps }}$
最大值为1
最后，为了最大限度地减少测试人员的主观偏见，他们同时评估在不同规模数据集上训练的多种策略；每次执行都是从这些多种策略中随机选择的，同时确保物体和机械臂的初始条件相同，从而在策略之间实现公平比较

1.2 数据扩展规律的揭示

1.2.1 对「对象泛化、环境泛化、及两者联合泛化」的结果和定性分析

在任务的设计上，主要是完成倒水和鼠标这两个操作任务：

在倒水任务中，机器人执行三个步骤：
首先，它抓住随机放置在桌子上的饮水瓶
其次，它将水倒入杯子中
最后，它将瓶子放在红色杯垫上。这个任务要求精确，特别是在将瓶口对准杯子时
在鼠标排列任务中，机器人完成两个步骤：它拾起鼠标并将其放置在鼠标垫上，使其正面朝前。鼠标可能倾斜，需要机器人使用非抓握动作（即推动）先将其对齐

在对象泛化上，他们在相同环境中使用32个不同的对象来收集每个对象120个演示，总共为每个任务提供3,840个演示。且经过SLAM过滤后，Pour Water和MouseArrangement的有效演示数量分别减少到3,765和3,820

为了研究训练对象数量如何影响策略对未见对象的泛化能力，他们从32个对象池中随机选择2m个对象进行训练，其中，
此外，为了检查策略性能如何随演示数量的变化而变化，他们为每个选定的对象随机抽样2n个有效演示的分数，其中，

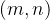
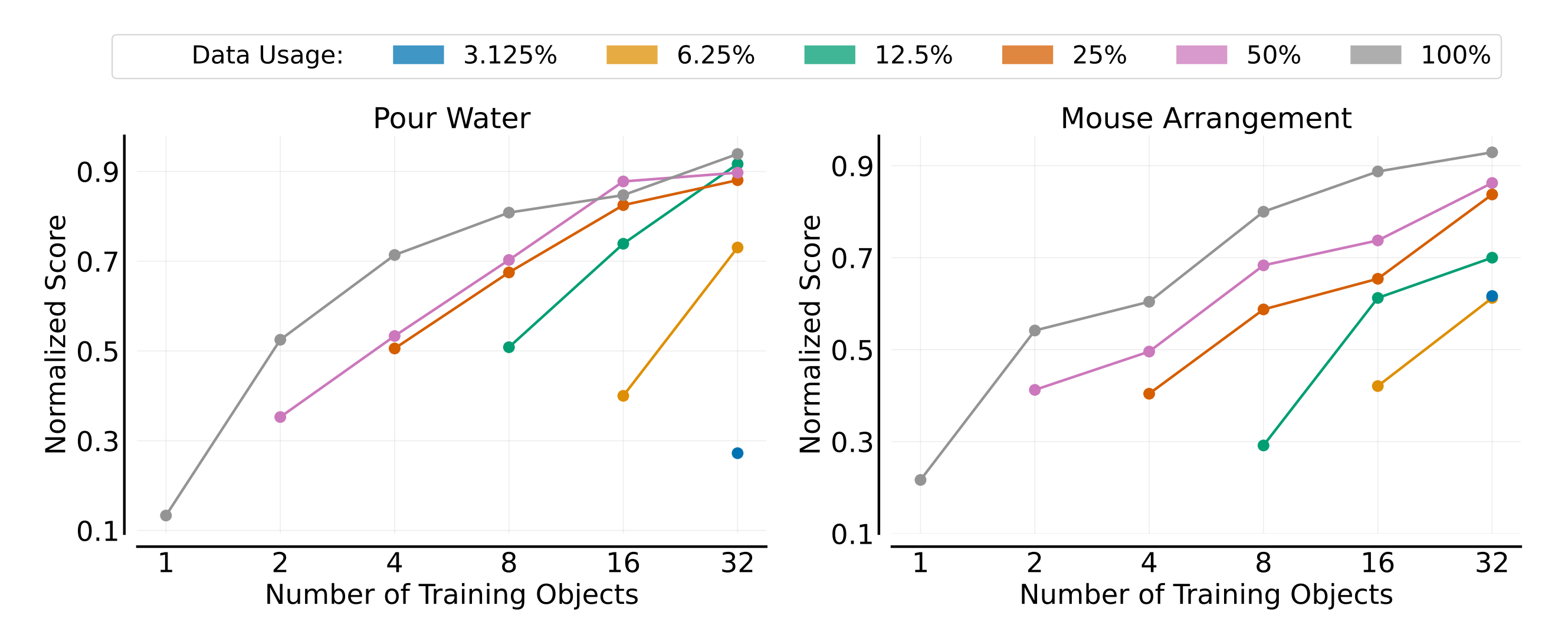
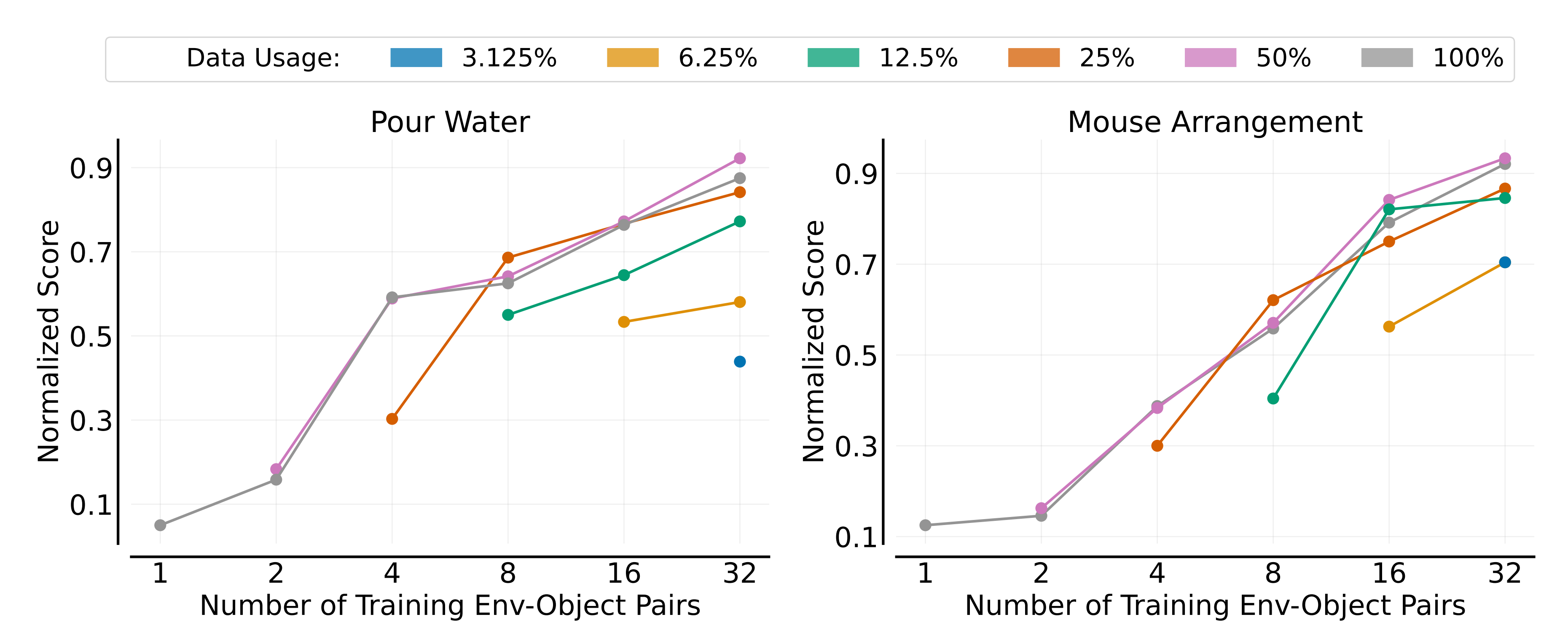
对于每个 (m, n) 的组合，如果总演示数量超过100，他们就训练一个策略。总共训练了21个策略，并在与训练数据相同的环境中使用8个未见对象进行评估，每个对象进行5次试验。每个策略的平均归一化得分在40次试验中报告

下图展示展示了两个任务的结果(每条曲线对应使用的不同演示比例，归一化分数显示为训练对象数量的函数)，可以得出几个关键观察：

随着训练对象数量的增加，策略在未见过对象上的表现随着示范比例的变化一致性提高
训练对象越多，每个对象所需的示范就越少
例如，在倒水任务中，使用8个对象进行训练时，使用12.5%示范的表现显著落后于使用100%示范的表现；然而，当使用32个对象进行训练时，这个差距几乎消失

换句话说，如果在都是8个对象训练时，12.5%示范比例下的表现远低于100%示范比例下的表现
但如果增加到32个对象进行训练时，12.5示范比例下的表现已经非常接近于100%示范比例下的表现
说明什么问题呢，说明随着对象数量的增加(比如从8个对象到32个对象)，即便在低示范比例下(比如12.5%)的表现也会非常不俗
总之，对象泛化相对容易实现
性能曲线的初始斜率非常陡峭：但在100%的示范比例之下，仅用8个训练对象时，两个任务的归一化得分就超过0.8，当训练对象数量达到32时，得分超过0.9
这些得分对应于已经很好地泛化到同一类别内任何新对象的策略

在环境泛化上，为了探索训练环境数量对泛化的影响，他们在32个不同环境中使用相同的操作对象，每个环境收集120次示范，故对于倒水和鼠标排列，这分别产生了3424和3351个有效示范，然后

他们从32个可用环境中随机选择m个环境「」进行训练，并且对于每个选择的环境，随机选择2n个有效示范「」的分数
每个策略在8个未见过的环境中使用与训练中相同的对象进行评估，每个环境进行5次试验

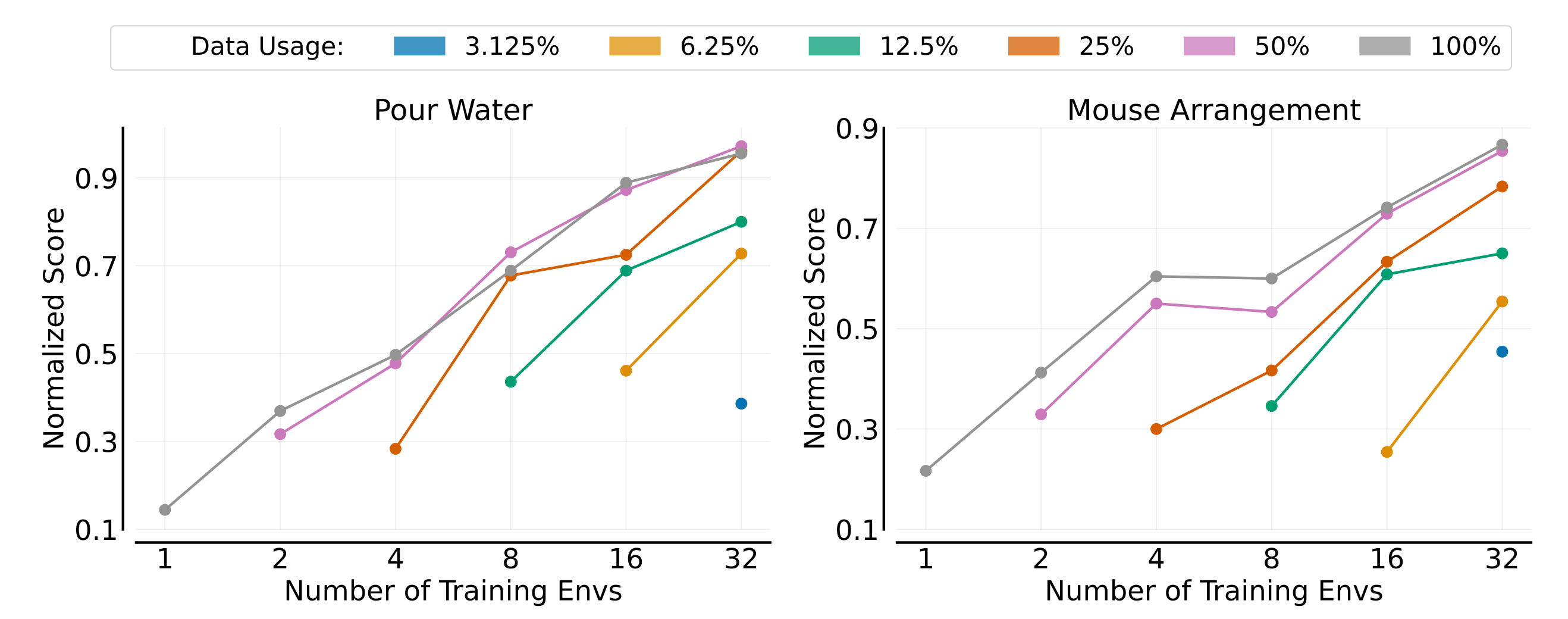
具体如下图所示(每条曲线对应于使用不同比例的演示，归一化分数显示为训练环境数量的函数)，可以看到

增加训练环境的数量可以提高策略在未见环境中的泛化性能。即使总演示次数保持不变，这一趋势仍然存在
说白了，训练环境的数量可以提高表现(同一演示比例之下，即在同一条颜色的线上，随着训练环境的数量增加而提高表现，看 ↗ )，且增加演示次数亦可提高表现(即同一训练环境数量下，不同颜色线的表现不同，看 ↑ )

然而，虽然在每个环境中增加演示的比例最初会提升性能，但这种改进很快就会减弱，正如代表50%和100%演示使用的线条，有很大程度的重叠
对于这两个任务来说，环境泛化似乎比对象泛化更具挑战性
比如，比较上图和上上图，可以观察到当环境或对象的数量较少时，增加环境的数量带来的性能提升小于增加对象的数量。这反映在环境泛化的性能曲线较低的斜率上

接下来，咱们看下环境和对象的联合泛化，即探讨一个训练环境和对象同时变化的设置

从32个环境中收集数据，每个环境配对一个独特的对象。对于倒水和鼠标排列，分别有3,648和3,564个有效演示
从32个环境对象对中随机选择2m对（m=0,1,2,3,4,5）进行训练，对于每个选定的对，随机抽取2n个有效演示的分数（n= 0,−1,−2,−3,−4,−5）。每个策略在8个未见过的环境中进行评估，每个环境使用两个未见过的对象，每个环境进行5次试验

如下图所示(每条曲线对应使用的不同演示比例，归一化分数显示为训练环境-对象对数的函数)，可以看到

增加训练环境-对象对的数量可以显著提高策略的泛化性能，这与之前的观察一致
有趣的是，尽管在新环境和对象中进行泛化更具挑战性，但在这种情况下，额外演示的收益饱和得更快（如25%和100%演示使用的重叠线所示）

这表明，与仅改变环境或对象相比，同时改变二者可以增加数据多样性，从而提高策略学习效率并减少对演示数量的依赖
这一发现进一步强调，扩展环境和对象的多样性比仅仅增加每个单独环境或对象的演示数量更有效

1.2.2 幂律拟合与定量分析

接下来，探讨实验结果是否遵循如在其他领域中所见的那种幂律缩放规律

具体而言，如果两个变量 Y 和 X 满足关系 $Y=\beta \cdot X^{\alpha 1}$ ，它们就表现出幂律关系
对 Y和 X 进行对数变换可揭示出线性关系： $\log (Y)=\alpha \log (X)+\log (\beta)$
在高阳团队的本次工作背景中，Y 代表最优性差距，定义为偏离最大分数的程度（即 1 − Normalized Score），而 X 可以表示环境、对象或演示的数量

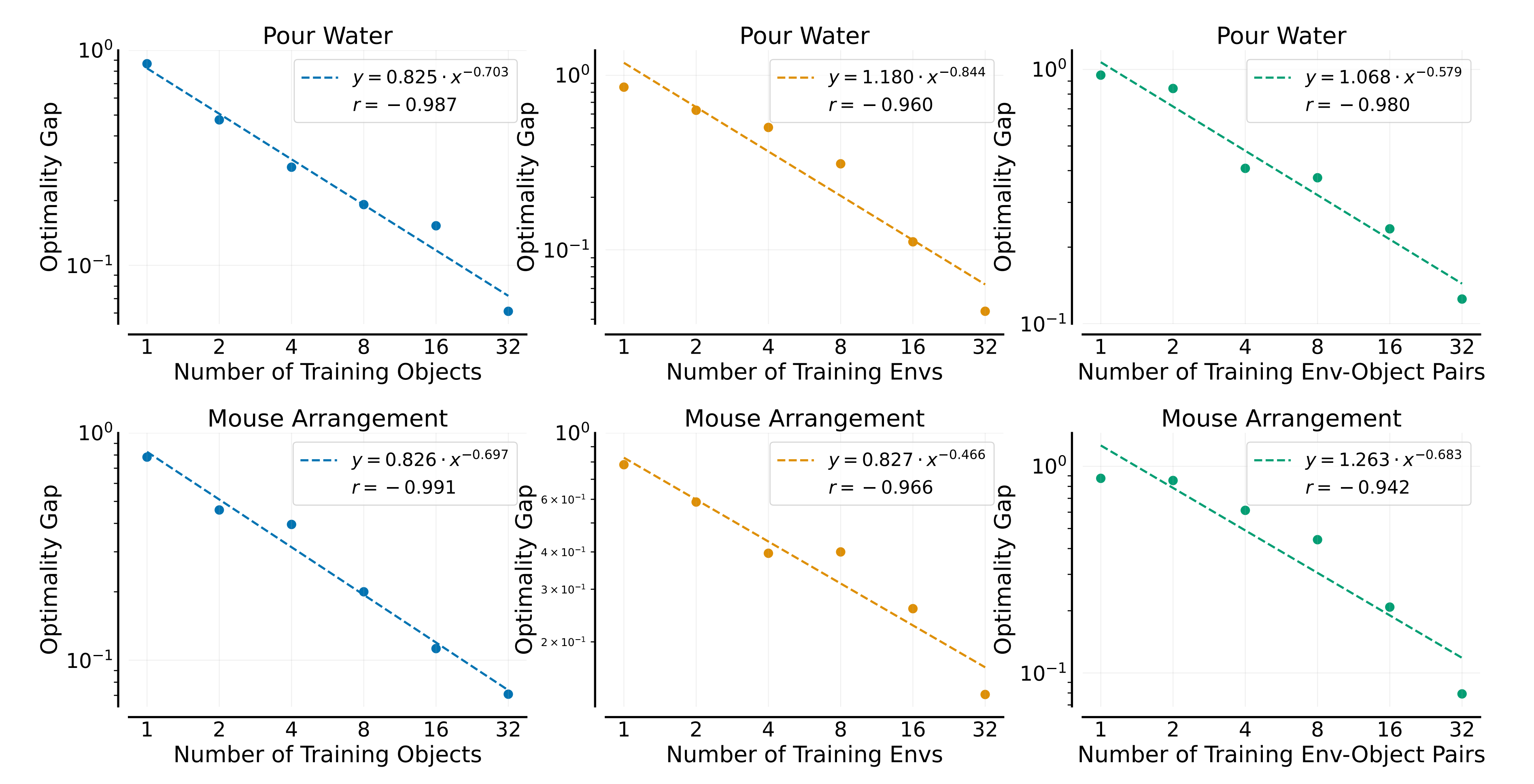
使用之前实验中 100% 演示比例的数据，对对数变换的数据拟合了一个线性模型，如下图所示(定义为图5)

基于所有结果，他们总结了以下数据缩放规律：

该策略对新对象、新环境或两者的泛化能力大致随着训练对象、训练环境或训练环境-对象对的数量呈幂律扩展
这可以通过上图中的相关系数来证明
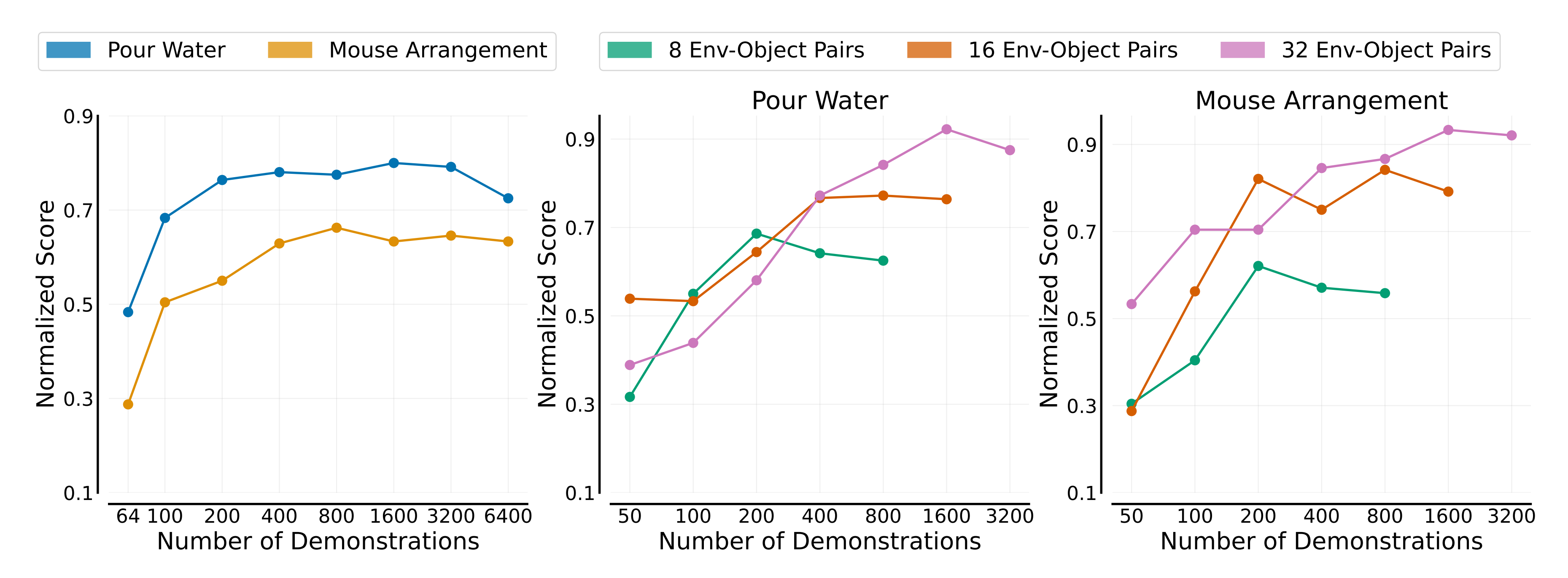
当环境和对象的数量固定时，示范次数与策略的泛化性能之间没有明显的幂律关系。虽然性能在增加示范次数时最初会迅速提高，但最终会趋于平稳，如下图最左侧的图所示
可以看到
上图左侧所示：在收集最大数量的示范的情况下，检查策略的性能是否与示范总数呈幂律关系。倒水和鼠标排列的相关系数分别为-0.62和-0.79，表明只有较弱的幂律关系
上图右侧所示：对于不同的环境-对象对，策略性能随着示范总数的增加而增加，然后达到饱和

关于环境和对象的这些幂律可以作为大规模数据的预测工具。例如，根据上上图：图5中的公式，他们预测，对于鼠标排列，要在新环境和对象上实现归一化得分0.99，需要1,191个训练环境-对象对，对此，july个人认为：这个结论便是这个工作比较有价值的点之一了

// 待更