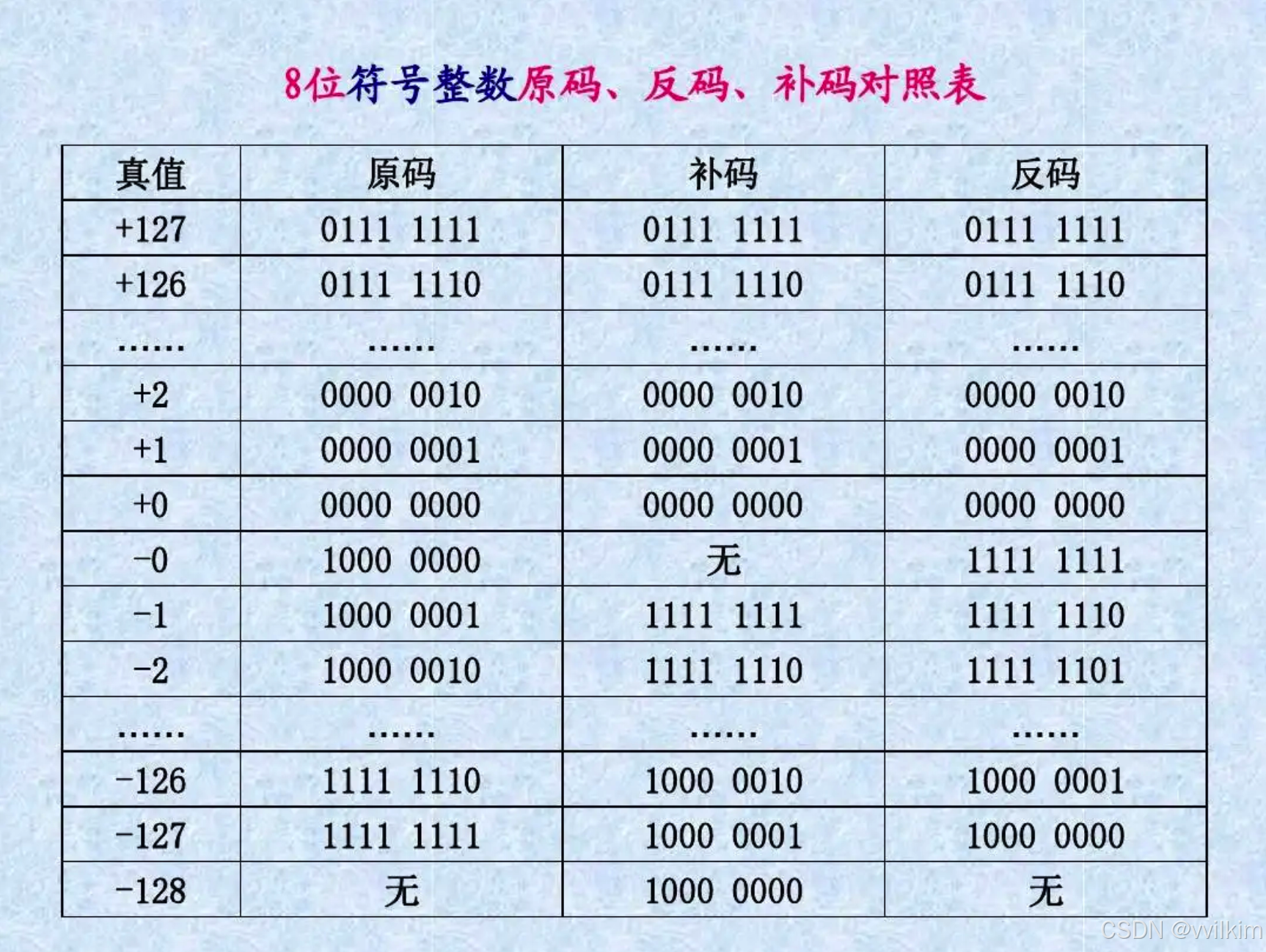
计算机系统中的数据表示方法多种多样，其中在整数的表示与运算中，原码、补码和反码是非常基础且重要的概念。这三种表示法不仅对于理解计算机底层工作原理至关重要，而且对于进行高效的数值运算也有着直接影响。它们之间有着密切的关系，同时也有各自的优缺点。

一、原码

1. 概念 原码是计算机中一种最直观的整数表示方法。它直接将二进制数表示成整数的绝对值，用最高位表示符号位，0表示正数，1表示负数。

2. 规则 假设一个字节（8位）用于存储一个整数，其中最高位为符号位，剩下7位为数值位。对于一个正整数，符号位为0，数值位按二进制表示法直接表示这个数的绝对值；对于一个负整数，符号位为1，数值位同样表示这个数的绝对值。

3. 使用 原码的使用主要体现在数据的存储上。但在进行加减运算时，原码的运算规则较为复杂，尤其是在处理负数的减法运算时，容易出现错误。因此，原码并不常用于直接的数值运算。

4. 示例 一个正整数+5的原码表示为：0000 0101
一个负整数-5的原码表示为：1000 0101

5. 缺点 加法和减法需要分别处理正数和负数，这种处理方式不够简洁

二、反码

1. 概念 反码是一种用于简化计算机中负数表示的方法。它是在原码的基础上，将符号位保持不变，其余位取反得到的。正数的反码与原码相同，负数的反码则是将原码的数值位按位取反。

2. 规则 以一个字节为例，正整数的反码与原码一致；负整数的反码则是将原码的数值位全部取反。例如，对于一个负数-5，其原码为1000 0101，则反码为1111 1010。

3. 使用 反码的使用可以简化符号位的处理过程，但由于反码中存在正零和负零两种表示形式，因此在实际应用中并不广泛采用。

4. 示例 一个正整数+5的反码表示为：0000 0101
一个负整数-5的反码表示为：1111 1010

5. 缺点 仍然存在加减法需要特殊处理的弊端

三、补码

1. 概念 补码是一种在计算机中存储和运算整数的方式，尤其适用于负数的运算。它在反码的基础上，对负数的最低位加1形成。补码不仅解决了零的唯一表示问题，而且简化了运算规则，使得计算机可以使用统一的操作处理加法和减法。

2. 规则 正数的补码与原码相同；负数的补码则是先将其原码转换为反码，再将反码的最低位加1得到。例如，对于一个负数-5，其原码为1000 0101，反码为1111 1010，补码为1111 1011。

3. 使用 补码是计算机中实际应用最广泛的一种数值表示法，尤其是在进行算术运算时，补码可以简化运算过程，保证运算结果的正确性。例如，计算机在执行加法运算时，无论操作数是正数还是负数，都可以直接使用补码进行运算，最终得到的结果也是补码表示的，只需将其转换为原码或者反码即可得到正确结果。

4. 示例 一个正整数+5的补码表示为：0000 0101
一个负整数-5的补码表示为：1111 1011

5. 缺点 存在一个最小值的负数溢出问题

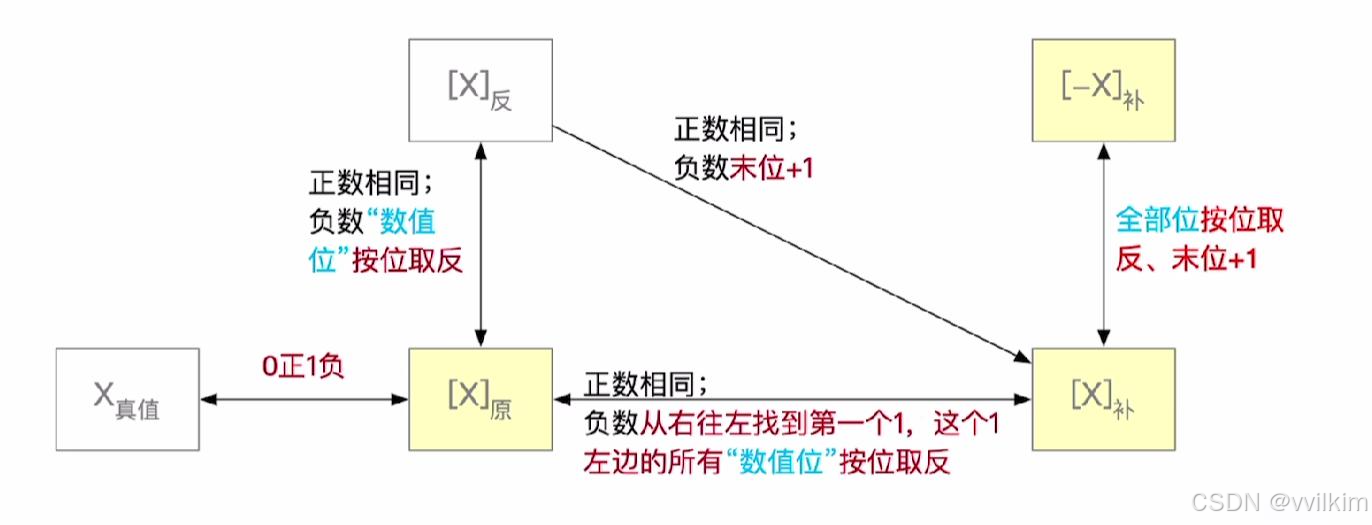
四、三者之间的关系

• 原码和反码：正数的原码和反码相同，负数的反码是在原码的基础上将数值位按位取反得到的。
• 反码和补码：正数的反码和补码相同，负数的补码是在反码的基础上将最低位加1得到的。
• 原码和补码：正数的原码和补码相同，负数的补码则是先取反码再对最低位加1得到的。

综上所述，原码、反码和补码是计算机中用于表示整数的三种基本方式，其中补码由于其简化运算规则和统一处理加减法的优势，在现代计算机系统中得到了广泛的应用。理解这三种码制及其相互之间的转换关系，对于深入学习计算机的底层工作原理和提高编程技巧有着重要的作用。