散列技术的关键问题在于设计散列函数和处理冲突。

4.2.1、散列函数

散列函数 建立由数据元素的关键字到该元素的存储位置的一种映射关系，声明如下：

int hash(int key);    
//散列函数，计算关键字为key元素的散列地址
//具体函数的实现有很多种。

将元素的关键字key作为散列函数的参数，散列函数值hash(key)就是该元素在散列表中的存储位置，也称散列地址。散列表的增删查操作都是根据散列地址获得元素的存储位置。

在实际应用中，散列表并没有设想的那么大，使之实现一对一的映射。散列函数通常是一个压缩映射，从关键字集合到地址集合是多对一的映射，所以会出现冲突。

4.2.2、冲突

设两个关键字k1，k2（k1 != k2）, 如果hash(K1) = hash(k2)，即它们的散列地址相同，表示不同关键字的多个元素映射到同一位置上（即两个不同的数据存放到同一块地址上），这种现象就是冲突。

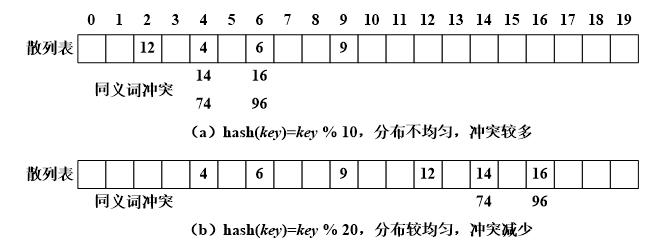
如下图，设关键字序列为{9,4,12,14,74,6,16,96}，散列容量为20，构造了两种方案（两种具体的散列函数实现）

冲突的产生频率与散列表容量、散列函数有关

增加散列表容量可以减少冲突，散列表装填因子：元素个数与容量之比，通常取值为0.75（扩容依据）

4.2.3、设计散列函数

一个好的散列函数的标准是，是散列地址均匀地分布在散列表中，尽量避免或减少冲突。

设计好的散列函数，需要考虑以下几方面因素：

• 散列地址必须均匀分布在散列表地全部地址空间
• 函数简单，计算散列函数花费时间为O(1)
• 使关键字的所有成分都起作用，以反映不同关键字的差异
• 数据元素的查找频率

因关键字的各种特性，因此，不存在一种散列函数对任何关键字集合都是最好的。在实际应用中，应根据具体情况，比较分析关键字与地址之间的对应关系，构造不同的散列函数，或将几种基本的散列函数组合起来使用，达到最佳效果。

几种常用的散列函数。

• 除留余数法

  • 除留余数法的散列函数如下，函数结果值范围为0 ~ prime-1

  • int hash(int key){   
     	return key%prime; 
    }
    

  • 除留余数法的关键在于prime 的取值。通常prime 取小于散列表长度的最大素数。

• 平方取中法

  • 将关键字值k的平方（k*k）的中间几位作为hash(K)的值，位数取决于散列表长度。例如：k=4731，k * k= 22382361，若表长为100，取中间两位，则hash(k)=82

• 折叠法

  • 将关键字分成几个部分，按照某种约定把几部分组合在一起

4.2.4、处理冲突

虽然好的散列函数可以使散列地址分布均匀，但只能减少冲突，而不能从根本上解决冲突。因此，散列表需要有一套措施，当冲突发生时能够有效地处理冲突。

处理冲突就是为产生冲突的元素再寻找一个有效的存储地址（这也是设计一个散列表的关键要点），介绍两种方法。

4.2.4.1、开放地址法

当产生冲突时，开放定址法在散列表内寻找另一个位置存储冲突的元素。 寻找位置的方法有线性探查法、二次探查法等多种。以下以线性探查法为例介绍开放定址法。

原理：设一个元素关键字为k，其散列地址为i=hash(k)，若散列表中i位置已存储元素，则产生冲突，探测下一个位置i+1是否为空，若空，则存储该元素；否则继续探测下一个位置i+2，以此类推，探测的地址序列是i+1、i+2、……直至找到一个空位置。

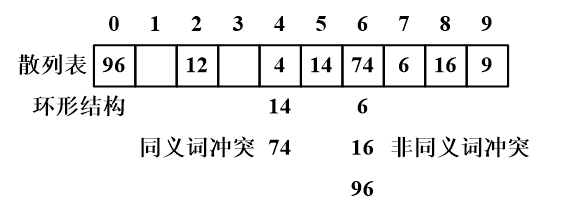
例如，设关键字序列为{9，4，12，14，74，6，16，96}， 散列函数为：hash(k) = k%10 ，采用线性探查法处理冲突所构造的散列表如下图所示。

在图中，4、14、74产生同义词冲突。存储14时，由于 i=hash(14)=4 位置已有元素，则将14存放于i+1位置，同理，将74存放于+2位置。由此造成的后果是，74占用了原本属于6的位置，使得74与6产生冲突，此时74与6并非同义词，称为非同义词冲突。

在采用线性探查法的散列表中查找关键字为k的元素，首先与散列表中 i=hash(k) 位置的元素比较关键字，如果相等，则查找成功；否则不能确定查找不成功，还要继续向后依次查找，此时蜕变为顺序查找，直到沿着环形结构找遍散列表中全部元素，才能确定查找不成功。

在采用线性探查法的散列表中不能删除元素，否则探测序列将中断，无法查找到产生同义词冲突的其他元素。线性探查法处理冲突的措施使非同义词也产生冲突，导致冲突增加，并堆积在散列表的一段区域，极速降低查找效率。
线性探查法存在缺陷的根本原因是，开放定址法在散列表内处理冲突，使得一个存储地址 i 可被任意一个元素抢占这样做破坏了散列函数i=hash(k)的规则。

4.2.4.2、链地址法(数组+链表)

以下采用链地址法处理冲突。

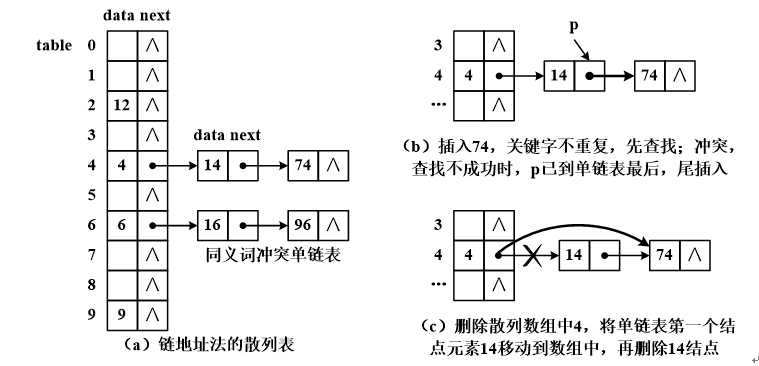
设关键字序列为{9，4，12，14，74，6，16，96}，散列表容量 length为10, 散列函数：hash(key)=key % length，构造散列表如下图所示。

原理：采用散列数组存储元素，将元素key存储在数组的hash(key)位置；采用一条同义词单链表存储一组同义词冲突元素，散列数组中各元素都可链接一条同义词单链表。因此，散列数组的元素类型是单链表的结点。 （这就是数组加链表）

对链地址法散列表的操作说明如下。

• 计算元素key的散列地址 i= hash(key) = key%length，采用除留余数法，计算地址时间为O(1)。
• 查找。比较散列数组table元素是否与key相等，若相等，则查找成功，比较1次；否则在第1条同义词单链表中查找，比较次数取决于key在单链表中位置。在上面所示散列表中，ASL成功 = （4×1+2×2+3×2）/8=1.75。
• 插入。由于散列函数不能识别关键字相同元素，因此，散列表不支持插入关键字重复元素。插入操作，先在散列数组中查找key，查找不成功插入；否则，有冲突再在同义词单链表中查找，查找不成功时，p已遍历到达单链表最后，尾插入key，如图(b)所示。
• 删除。先查找，查找成功后再删除。如果要删除散列数组中的元素，则要将同义词单链表的第一个结点元素移动到散列数组中，再删除同义词单链表的第一个结点，如图©所示，此删除操作与单链表删除结点操作不同，麻烦许多。

散列表的操作效率取决于单链表的操作效率。同义词单链表是动态的，冲突越多，链表越长。因此，要设计好的散列函数使数据元素尽量均匀分布，同义词单链表越短越好。

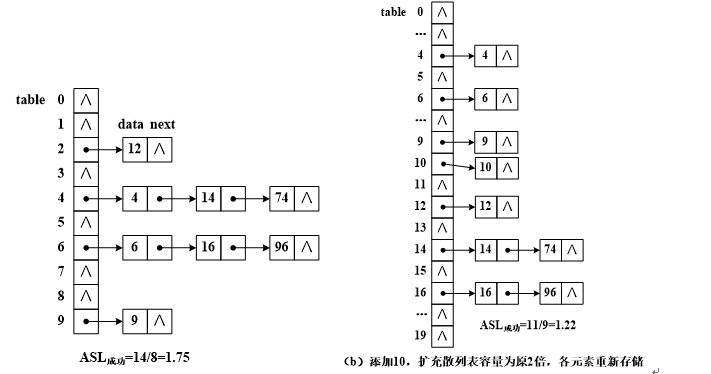
为了避免删除操作时移动元素，将上图(a)链地址法散列表改进成如下图(a)所示，散列表元素是同义词单链表对象，散列表的查找、插入、删除等操作，则转化为单链表的查找、插入、删除等操作，算法简洁明了。当“元素个数=散列表容量×装填因子”时，表示散列表满，需要扩充数组容量。申请另一个2倍容量的数组，将元素移动到扩容数组中，如下图(b)所示。

注意：由于散列数组容量length增大2倍，各元素的散列地址也随之改变，缩短了同义词单链表。

下面是构造链地址法的散列表的一些代码。其中，成员变量table表示散列数组，元素是SinglyList< T>对象，表示同义词单链表。散列函数hash（X）采用除留余数法。

public class HashSet<T>  //implements Set<T> // 散列表类，采用链地址法
    {
        private SinglyList<T>[] table;                          //散列表，同义词单链表对象数组    
        private int count = 0;                                 //元素个数    
        private static final float LOAD_FACTOR = 0.75f;        //装填因子，元素个数与容量之比
        private static final float MIN_CAPACITY = 16;          //默认最小容        

        public HashSet(int length)                             //构造容量为length的散列表    
        {
            if (length < 10)
                //为了图8.12和图8.14 
                length = 10;                                     //设置最小容量    	
            this.table = new SinglyList[length];
            for (int i = 0; i < this.table.length; i++)
                this.table[i] = new SinglyList<T>();           //构造空单链表
            this.enlarge(capacity);
        }

        public HashSet()                                       //构造空散列表，默认容量    
        {
            this(16);
        }

        //散列函数，计算关键字为x元素的散列地址。若x==null，Java抛出空对象异常
        private int hash(T x) {
            int key = Math.abs(x.hashCode());              //每个对象的hashCode()方法返回int        
            return key % this.table.length;                  //除留余数法，除数是散列表容量    
        }

        public T search(T key)             //返回查找到的关键字为key元素，若查找不成功返回null
        {
            //在单链表中查找关键字为key元素        
            Node<T> find = this.table[this.hash(key)].search(key);
            return find == null ? null : find.data;
        }

        public boolean add(T x)                        //插入x元素，若x元素关键字重复，则不插入
        {
            if (this.count > this.table.length * LOAD_FACTOR)      //若散列表满，则扩充容量        
            {
                this.printAll();
                System.out.print("\n添加" + x + "，");
                SinglyList<T>[] temp = this.table;             //散列表，同义词单链表对象数组            
                this.table = new SinglyList[this.table.length * 2];
                for (int i = 0; i < this.table.length; i++) this.table[i] = new SinglyList<T>();
                this.count = 0;
                //遍历原各同义词单链表，添加原所有元素            
                for (int i = 0; i < temp.length; i++)
                    for (Node<T> p = temp[i].head.next; p != null; p = p.next) this.add(p.data);
            }
            boolean insert = this.table[this.hash(x)].insertDifferent(x) != null;
            if (insert)                                        //单链表尾插入关键字不重复元素            
                this.count++;
            return insert;                //第5版??    
            
            /*
             // 也可   T find = this.search(x);                           
            //  查找 //查找不成功插入关键字不重复元素，单链表头插入，反序。？？不需要insertDifferent(x)        
            if (find == null) {
                this.table[this.hash(x)].insert(0, x);
                this.count++;
                return true;
            }
            return false;      
            */
        }

        public T remove(T key)                           //删除关键字为key元素，返回被删除元素
        {
            T x = this.table[this.hash(key)].remove(key);      //同义词单链表删除key元素结点        
            if (x != null) this.count--;
            return x;
        }

        //以下方法体省略，    
        // 构造散列表，由values数组提供元素集合    
        public HashSet(T[] values) {
            this((int) (values.length / HashSet.LOAD_FACTOR));    //构造指定容量的空散列表        
            this.addAll(values);                               //插入values数组所有元素    
        }

        public int size()                                      //返回元素个数    
        {
            return count;
        }

        public boolean isEmpty()                               //判断是否为空    
        {
            return this.size() == 0;
        }

        public boolean contains(T key)                         //判断是否包含关键字为key元素    
        {
            return this.search(key) != null;
        }

        public void addAll(T[] values)                         //插入values数组所有元素    
        {
            for (int i = 0; i < values.length; i++)
                this.add(values[i]);                           //插入元素    
        }

        public void clear()                                    //删除所有元素    
        {
            for (int i = 0; i < this.table.length; i++)            //遍历各同义词单链表            
                this.table[i].clear();
        }

        public String toString()                              //返回散列表所有元素的描述字符串    
        {
            String str = this.getClass().getName() + "(";
            boolean first = true;
            for (int i = 0; i < this.table.length; i++)            //遍历各同义词单链表            
                for (Node<T> p = this.table[i].head.next; p != null; p = p.next) {
                    if (!first) str += ",";
                    first = false;
                    str += p.data.toString();
                }
            return str + ")";
        }

        public void printAll()                             //输出散列表的存储结构，计算ASL成功    
        {
            System.out.println("散列表：容量=" + this.table.length + "，" + this.count + "个元素" + "，hash(key)=key % " + this.table.length + "，" + this.toString());
            for (int i = 0; i < this.table.length; i++)            //遍历各同义词单链表            
                System.out.println("table[" + i + "]=" + this.table[i].toString());
            System.out.print("ASL成功=(");
            int asl = 0;
            for (int i = 0; i < this.table.length; i++)            //遍历各同义词单链表        
            {
                int j = 1;
                for (Node<T> p = this.table[i].head.next; p != null; p = p.next, j++) {
                    System.out.print((asl == 0 ? "" : "+") + j);
                    asl += j;
                }
            }
            if (count == 0) System.out.println(") = 0\n");
            else System.out.println(")/" + count + " =" + asl + "/" + count + " =" + ((asl + 0.0) / count) + "\n");
        }

        //以下教材没写    
        // 不行  
        public T[] toArray()                              //返回包含集合所有元素的数组    

        public Object[] toArray()                              //返回包含集合所有元素的数组    
        {
            Object[] values = new Object[this.size()];
            int j = 0;
            for (int i = 0; i < this.table.length; i++)            //遍历各同义词单链表            
                for (Node<T> p = this.table[i].head.next; p != null; p = p.next) values[j++] = p.data;
            return values;
        }

        public void enlarge(int length)                        //散列表扩充容量为capacity    
        {
            this.table = new SinglyList[length];
            for (int i = 0; i < this.table.length; i++) this.table[i] = new SinglyList<T>();           //构造空单链表    
        }
    }