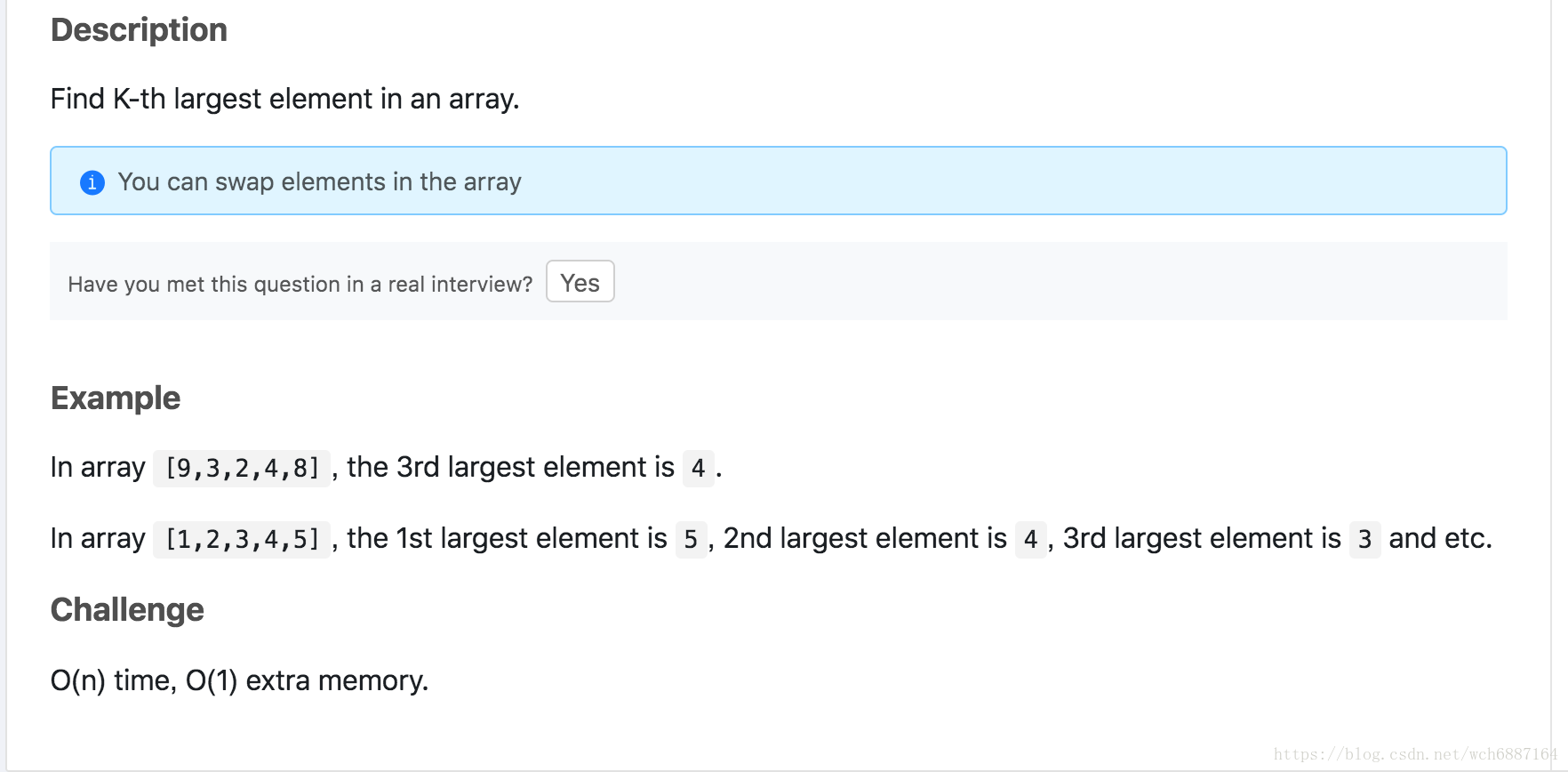
问题一、未排序数组找中位数

     1未排序数组kth大的数

class Solution {
    /*
     * @param k : description of k
     * @param nums : array of nums
     * @return: description of return
     */
    public int kthLargestElement(int k, int[] nums) {
      return help(nums,nums.length-k+1,0,nums.length-1);
    }
    
    public int help(int[] nums,int k,int begin,int end){
        if(begin==end)
        return nums[begin];
        int mid = begin+(end-begin)/2;
        int key = nums[mid];
        int i = begin,j= end;
        while(i<=j){
            while(i<=j&&nums[j]>key)
            j--;
             while(i<=j&&nums[i]<key)
            i++;
            if(i<=j){
                int temp = nums[i];
                nums[i] = nums[j];
                nums[j] = temp;
                i++;
                j--;
            }
        }
        if(begin+k-1<=j)
        return help(nums,k,begin,j);
        if(begin+k-1>=i)
        return help(nums,k-(i-begin),i,end);
        return nums[i-1];
       
    }
    
   
};

中位数：

            直接调用这个函数，把K换成二分之一长度就可以了。

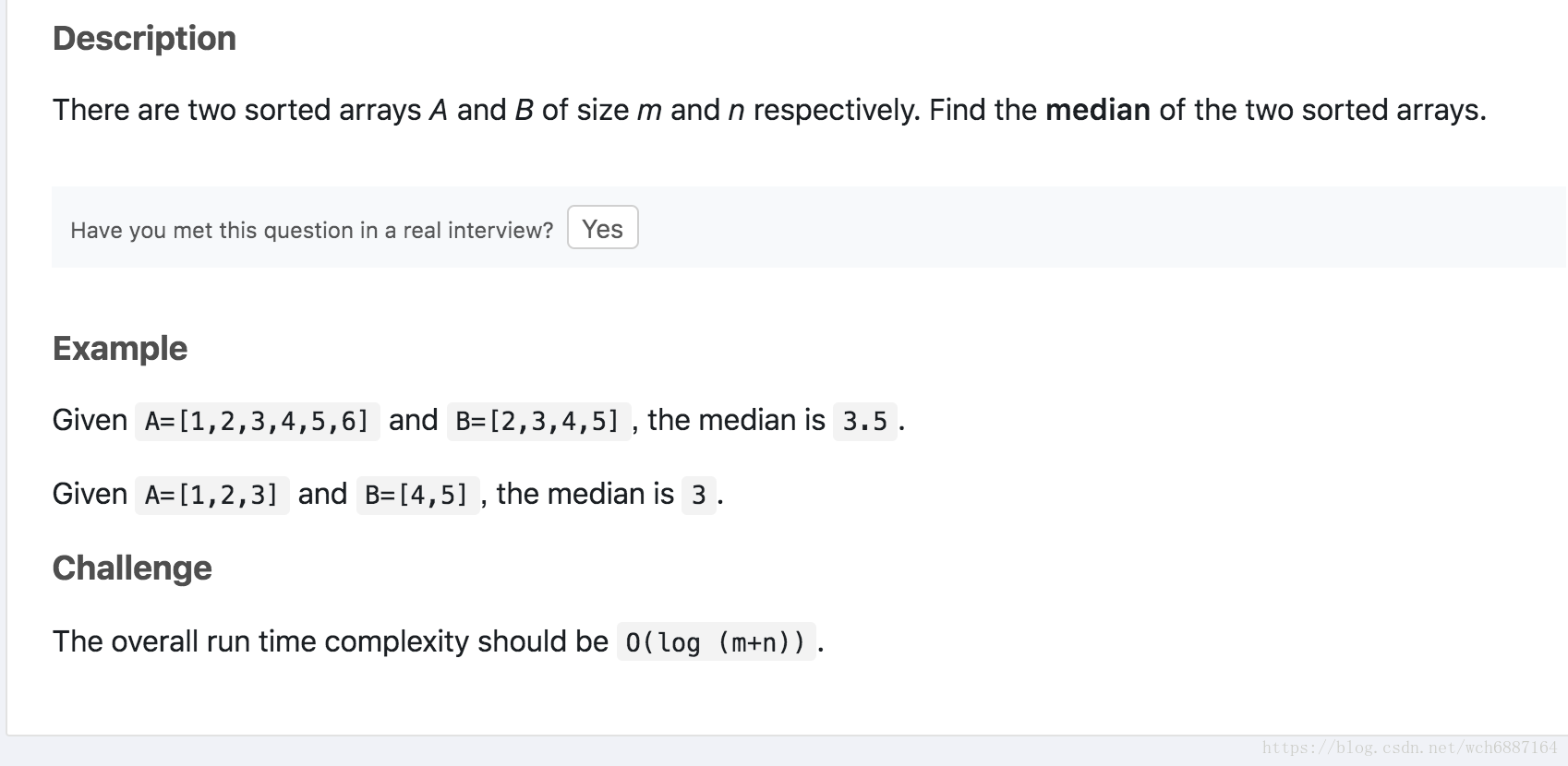
问题二、median-of-two-sorted-arrays

思路：砍，每次砍中位数小的数组一般，直到最后砍到k为1就可以返回结果。

public class Solution {
    /*
     * @param A: An integer array
     * @param B: An integer array
     * @return: a double whose format is *.5 or *.0
     */
    public double findMedianSortedArrays(int[] A, int[] B) {
        // write your code here
        int len = A.length+B.length;
        if(len%2!=0)
        return findMedianSortedArraysCore(A,0,B,0,len/2+1);
        else
        return (findMedianSortedArraysCore(A,0,B,0,len/2)+findMedianSortedArraysCore(A,0,B,0,len/2+1))/2.0;
    }
    
    public double findMedianSortedArraysCore(int[] A,int Abegin,int[] B,int BBegin,int k){
        if(Abegin>=A.length)
        return B[BBegin+k-1];
        if(BBegin>=B.length)
        return A[Abegin+k-1];
        
       if(k==1)
       return Math.min(A[Abegin],B[BBegin]);
       
       int Akey = Abegin+k/2-1<A.length?A[Abegin+k/2-1]:Integer.MAX_VALUE;
       int Bkey = BBegin+k/2-1<B.length?B[BBegin+k/2-1]:Integer.MAX_VALUE;
       
       if(Akey<Bkey)
        return findMedianSortedArraysCore(A,Abegin+k/2,B,BBegin,k-k/2);
          return findMedianSortedArraysCore(A,Abegin,B,BBegin+k/2,k-k/2);
    }
}