相关链接:
noip2017是我见过的有史以来最坑爹的一场考试了。
今年北京市考点有一个是我们学校,我还恰好被分到了自己学校(还是自己天天上课的那个教室),于是我同时报了普及提高,一天半的时间都考了。
这次考试总的来说基本上都爆炸了。虽然都拿了一等奖,但这根本不能说明问题,从中可以看出我在敲代码学习上还是问题百出。
下面我分两篇来总结一个kubi的OIer的解题思路及心得,当然包括正解。然而我莫名其妙的打了好长好长……难道我太勤奋了?
OIer常识:本文所有log均以2为底
普及组
今年的普及组题目很不良心,我考试的时候周围全是小学生和初一学生。。。我是少有的几个初三学生中的一个。
普及组的题目,我本来计划ak虐场的,结果被反虐了。不是题不会(每题都是一眼就看出怎么做),而是编程问题百出啊!哎。
1.成绩
题目描述
牛牛最近学习了C++入门课程,这门课程的总成绩计算方法是:
总成绩=作业成绩×20%+小测成绩×30%+期末考试成绩×50%
牛牛想知道,这门课程自己最终能得到多少分。
输入输出格式
输入格式
输入文件只有1行,包含三个非负整数A、B、C,分别表示牛牛的作业成绩、小测成绩和期末考试成绩。相邻两个数之间用一个空格隔开,三项成绩满分都是100分。
输出格式:
输出文件只有1行,包含一个整数,即牛牛这门课程的总成绩,满分也是100分。
输入输出样例
输入样例#1:
100 100 80
输出样例#1:
90
输入样例#2:
60 90 80
输出样例#2:
79
说明
输入输出样例1说明
牛牛的作业成绩是100分,小测成绩是100分,期末考试成绩是80分,总成绩是100×20%+100×30%+80×50%=20+30+40=90。
输入输出样例2说明
牛牛的作业成绩是60分,小测成绩是90分,期末考试成绩是80分,总成绩是60×20%+90×30%+80×50%=12+27+40=79。
数据说明
对于30%的数据,A=B=0。
对于另外30%的数据,A=B=100。
对于100%的数据,0≤A、B、C≤100且A、B、C都是10的整数倍。
10秒题
#include<iostream>
#include<cstdio>
using namespace std;
inline int read(){
int x=0; bool f=1; char c=getchar();
while(!isdigit(c)){if(c=='-') f=0; c=getchar();}
while(isdigit(c)){x=x*10+c-'0'; c=getchar();}
if(!f) return 0-x;
return x;
}
int a,b,c;
int main(){
a=read(),b=read(),c=read();
printf("%d",a/5+b/10*3+c/2);
return 0;
}
我对计算机的数据精度还是比较了解的,因此我没有想乘以零点几,而是a/10*2+b/10*3+c/10*5。
这是正常想法,但是很多小学生开了int a,b,c之后不知道这一点,因此直接写a*0.2+b*0.3+c*0.5。由于这个原因,官方11月22号重测了一次这题,不过用新数据测还是只能过官方数据的60分。
但如果开double a,b,c,然后写a*0.2+b*0.3+c*0.5,直接输出这个浮点结果好像也可以AC官方数据。
我的得分:100
2.图书管理员
题目描述
图书馆中每本书都有一个图书编码,可以用于快速检索图书,这个图书编码是一个 正整数。 每位借书的读者手中有一个需求码,这个需求码也是一个正整数。如果一本书的图书编码恰好以读者的需求码结尾,那么这本书就是这位读者所需要的。 小 D 刚刚当上图书馆的管理员,她知道图书馆里所有书的图书编码,她请你帮她写 一个程序,对于每一位读者,求出他所需要的书中图书编码最小的那本书,如果没有他 需要的书,请输出-1。
输入输出格式
输入格式:
输入文件的第一行,包含两个正整数 n 和 q,以一个空格分开,分别代表图书馆里 书的数量和读者的数量。
接下来的 n 行,每行包含一个正整数,代表图书馆里某本书的图书编码。
接下来的 q 行,每行包含两个正整数,以一个空格分开,第一个正整数代表图书馆 里读者的需求码的长度,第二个正整数代表读者的需求码。
输出格式:
输出文件有 q 行,每行包含一个整数,如果存在第 i 个读者所需要的书,则在第 i 行输出第 i 个读者所需要的书中图书编码最小的那本书的图书编码,否则输出-1。
输入输出样例
输入样例#1:
5 5
2123
1123
23
24
24
2 23
3 123
3 124
2 12
2 12
输出样例#1:
23
1123
-1
-1
-1
说明
【数据规模与约定】
对于 20%的数据,1 ≤ n ≤ 2。
另有 20%的数据,q = 1。
另有 20%的数据,所有读者的需求码的长度均为 1。
另有 20%的数据,所有的图书编码按从小到大的顺序给出。
对于 100%的数据,1 ≤ n ≤ 1,000,1 ≤ q ≤ 1,000,所有的图书编码和需求码均 不超过 10,000,000。
不得不说这题简直不是一般的水。noip2016普及组的t2(回文日期)那道题都比这难写(主要是那题不好过回文思路)。其实普及组第二题就是这样一个事情,往简单想就好做,往复杂想就难做。
本来我是想打一棵trie的,结果我一看数据就喷了,对于每个询问直接O(n)遍历,5分钟过掉。
#include<iostream>
#include<cstdio>
#include<cmath>
using namespace std;
inline int read(){
int x=0; bool f=1; char c=getchar();
while(!isdigit(c)){if(c=='-') f=0; c=getchar();}
while(isdigit(c)){x=x*10+c-'0'; c=getchar();}
if(!f) return 0-x;
return x;
}
int n,q,a[1002],len,query,mod,ans;
int main(){
n=read(),q=read();
int i,j;
for(i=1;i<=n;i++) a[i]=read();
for(i=1;i<=q;i++){
len=read(),query=read();
mod=pow(10,len); //pow(10,len)=10的len次方
ans=2147483647;
for(j=1;j<=n;j++) if(a[j]%mod==query) ans=min(ans,a[j]);
if(ans==2147483647) printf("-1\n");
else printf("%d\n",ans);
}
return 0;
}
图书编码都没超过int,查询时直接把每个编码取模判断后面的位就好了,要是图书编码是超长字符串的话恐怕就得用到诸如trie或后缀数组之类的东西来查询了。没办法,普及组就得水一水。
2018.10.6 update:注意到图书编码最大$10^7$,可以用桶存一个后缀对应的书的最小编号,将每本书的每个后缀在桶中的对应位置更新即可。这个方法时间复杂度小,空间复杂度大。
另外考场上很多人(包括我旁边那位初三学生!)都花了1小时打这题,我当时不明白,考后问他们怎么做的,结果他们都往复杂想了,写了排序之类的各种奇怪方法。我没明白他们怎么想的,但我也懒得去把自己往复杂的沟里拖。
我的得分:100
3.棋盘
题目描述
有一个m × m的棋盘,棋盘上每一个格子可能是红色、黄色或没有任何颜色的。你现在要从棋盘的最左上角走到棋盘的最右下角。
任何一个时刻,你所站在的位置必须是有颜色的(不能是无色的), 你只能向上、 下、左、 右四个方向前进。当你从一个格子走向另一个格子时,如果两个格子的颜色相同,那你不需要花费金币;如果不同,则你需要花费 1 个金币。
另外, 你可以花费 2 个金币施展魔法让下一个无色格子暂时变为你指定的颜色。但这个魔法不能连续使用, 而且这个魔法的持续时间很短,也就是说,如果你使用了这个魔法,走到了这个暂时有颜色的格子上,你就不能继续使用魔法; 只有当你离开这个位置,走到一个本来就有颜色的格子上的时候,你才能继续使用这个魔法,而当你离开了这个位置(施展魔法使得变为有颜色的格子)时,这个格子恢复为无色。
现在你要从棋盘的最左上角,走到棋盘的最右下角,求花费的最少金币是多少?
输入输出格式
输入格式:
数据的第一行包含两个正整数 m, n,以一个空格分开,分别代表棋盘的大小,棋盘上有颜色的格子的数量。
接下来的 n 行,每行三个正整数 x, y, c, 分别表示坐标为( x, y)的格子有颜色 c。
其中 c=1 代表黄色, c=0 代表红色。 相邻两个数之间用一个空格隔开。 棋盘左上角的坐标为( 1, 1),右下角的坐标为( m, m)。
棋盘上其余的格子都是无色。保证棋盘的左上角,也就是( 1, 1) 一定是有颜色的。
输出格式:
输出一行,一个整数,表示花费的金币的最小值,如果无法到达,输出-1。
输入输出样例
输入样例#1:
5 7
1 1 0
1 2 0
2 2 1
3 3 1
3 4 0
4 4 1
5 5 0
输出样例#1:
8
输入样例#2:
5 5
1 1 0
1 2 0
2 2 1
3 3 1
5 5 0
输出样例#2:
-1
说明
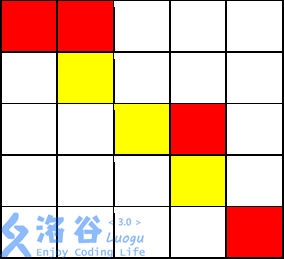
输入输出样例 1 说明
从( 1, 1)开始,走到( 1, 2)不花费金币
从( 1, 2)向下走到( 2, 2)花费 1 枚金币
从( 2, 2)施展魔法,将( 2, 3)变为黄色,花费 2 枚金币
从( 2, 2)走到( 2, 3)不花费金币
从( 2, 3)走到( 3, 3)不花费金币
从( 3, 3)走到( 3, 4)花费 1 枚金币
从( 3, 4)走到( 4, 4)花费 1 枚金币
从( 4, 4)施展魔法,将( 4, 5)变为黄色,花费 2 枚金币,
从( 4, 4)走到( 4, 5)不花费金币
从( 4, 5)走到( 5, 5)花费 1 枚金币
共花费 8 枚金币。
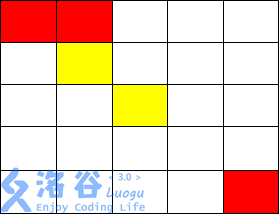
输入输出样例 2 说明
从( 1, 1)走到( 1, 2),不花费金币
从( 1, 2)走到( 2, 2),花费 1 金币
施展魔法将( 2, 3)变为黄色,并从( 2, 2)走到( 2, 3)花费 2 金币
从( 2, 3)走到( 3, 3)不花费金币
从( 3, 3)只能施展魔法到达( 3, 2),( 2, 3),( 3, 4),( 4, 3)
而从以上四点均无法到达( 5, 5),故无法到达终点,输出-1
数据规模与约定
对于 30%的数据, 1 ≤ m ≤ 5, 1 ≤ n ≤ 10。
对于 60%的数据, 1 ≤ m ≤ 20, 1 ≤ n ≤ 200。
对于 100%的数据, 1 ≤ m ≤ 100, 1 ≤ n ≤ 1,000。
这题给多数人的第一印象就是不好做的搜索题目。
其实这题跟noip2016普及组t3(海港)相比确实多了一定的复杂性,去年那题可以直接用STL提供的queue(队列)存储人员,等同于没考算法。而这道题需要一点最短路知识。
做这道题之前一定要先搞明白一个事情:那就是题目中的给白色格子施魔法,就相当于可以“跨”过一个白色格子,给白色格子花2金币施魔法填颜色后,为了让金币花费尽量小,当然要用最优策略:如果跨过白色格子连接的两个格子颜色相同,那白色格子肯定会填成跟两侧格子一样的颜色;如果两个格子颜色不同,那白色格子填红/黄哪种颜色都行,因为肯定会与两个格子中的一个颜色不同从而要多花1金币通行。
我在考场上第一眼就想到了dfs。不过很不幸,10分钟打完的dfs在m=100的情况下TLE了,我当时并没有考虑更换记忆化搜索,而是改道bfs,写+调了50分钟。下面我回忆一下怎么想的bfs吧。
如果你还不会这道题,请拿起笔和纸,画格子模拟一下我下面说的做法。图是最好的辅助工具。
做法1:bfs
没学过bfs的一定要先百度去普及普及(大多数人都应该学过吧?)用一个队列记录从当前格子(从队列中取出的当前点一定是红/黄格子)往周围4格扩展的情况(包括格子的x、y坐标位置以及到达该格子时花费的金币数)。
对于周围的红/黄格子直接放入队列并判断如果和当前格子颜色相同(上面说了队列中存的都是红黄节点,白色节点马上会提)就将当前格子的金币花费代入目标格子的金币花费,否则将当前格子的金币花费+1代入目标格子的金币花费。然后把目标格子的信息推入队列;对于周围的白色格子,要再以这个白色格子出发向其另外三个方向的邻格子扩展,如果目标格子是红/黄格子,由于要跨过一个白色格子,需要花2金币施魔法,因此在判断与当前格子(即一开始从队列中取出的格子)颜色是否相同后(颜色相同不加金币花费,颜色不同金币花费+1),还要额外给金币花费+2。然后把目标格子的信息推入队列。而如果目标格子还是白色格子,魔法是不能连跨两个白色格子的,因此直接返回寻找其它方向的邻格子,目标格子不推入队列。
如果从队列中取出的格子是右下角的终点,就用它的金币花费更新ans,ans应当尽量小。如果队列被取空了,终点还没有更新过一次答案(infinity,俗称inf),那就说明从起点怎么扩展也到达不了终点,答案就是-1。
根据上面的思路,队列中一定只存了红黄节点,白色节点都是特判能否施魔法跳过的。
另外,上面的做法不带优化,因为一个格子可能会从多个方向被扩展到,而大多数情况下后被扩展到的时候金币花费都比原先更大(因为扩展次数增多了,走过的格子也就更多了嘛,金币基本不可能更少花),因此在扩展到一个可以放入队列的目标点时(即红/黄格子),要判断本次扩展到目标点的金币花费是否比目标点的历史金币花费大,如果更大则直接返回,不将其推入队列(因为这样既浪费时间又可能导致答案错误)。这就是搜索的基本优化。
这个思路本身没问题,因为bfs+上述优化的时间复杂度已经足够小了,对于m=100的数据也能秒算,但是上述算法忽略了一个小问题,并且正是因为这个问题,我被官方数据卡掉了50分T_T。(民间数据就TMD AC)。
如果右下角的终点是白格子,那么这种做法就永远都跳过终点了,导致无答案(-1)。因此要特判一下如果从终点旁边扩展到了终点,就直接算出到终点的金币花费并更新ans。
这种做法亲测可过,且跑得巨快无比,在洛谷上跑的所有点都是0ms。不妨想想嘛,最多有100*100=10000个格子,而且对于测评数据而言,绝大多数格子通常都是白色的,那么剩下的红/黄格子根据上面所述的优化(即对于一个格子,大多数情况下后被扩展到的时候金币花费都比原先更大),每格几乎只会往队列中放入一次,也就是说均摊的时间复杂度比O(m²)要小的多!对搜索有深入了解的人应该明白。
即使所有格子都是红/黄色的,每个格子依然几乎只会往队列中放入一次,均摊的O(m²)时间复杂度依然可以虐题。
#include<iostream>
#include<cstdio>
#include<cstring>
#include<queue>
#define maxm 102
#define inf 0x3f3f3f3f
using namespace std;
inline int read(){
int x=0; bool f=1; char c=getchar();
while(!isdigit(c)){if(c=='-') f=0; c=getchar();}
while(isdigit(c)){x=x*10+c-'0'; c=getchar();}
if(!f) return 0-x;
return x;
}
struct xy{
int x,y;
}tmp;
int fx[4][2]={{0,1},{1,0},{0,-1},{-1,0}};
int dp[maxm][maxm],m,n,col[maxm][maxm];
/*
void dfs(int x,int y,int facol,bool magic,int coin){ //考场上首打的超时dfs
if(x==m && y==m){ans=min(ans,coin); return;}
int i,j,gx,gy;
vis[x][y]=1;
for(i=0;i<4;i++){
gx=x+fx[i][0],gy=y+fx[i][1];
if(gx<1 || gx>m || gy<1 || gy>m) continue;
if(vis[gx][gy]) continue;
printf("%d %d->%d %d\n",x,y,gx,gy);
if(!col[gx][gy]){//鏃犺壊鏍煎瓙
if(magic) continue;//涓嶈兘杩炵画鑶滄硶
dfs(gx,gy,col[x][y],1,coin+2);
continue;
}
if(facol==col[gx][gy]) dfs(gx,gy,col[x][y],0,coin);//鏍煎瓙棰滆壊鐩稿悓
else dfs(gx,gy,col[x][y],0,coin+1);
}
vis[x][y]=0;
}
*/
queue<xy>q; //
int main(){
memset(dp,inf,sizeof(dp));
m=read(),n=read();
int i,j,x,y,z,gx,gy,_gx,_gy;
for(i=1;i<=n;i++){
x=read(),y=read(),z=read();
if(z==0) col[x][y]=-1;
else col[x][y]=1;
}
q.push((xy){1,1});
dp[1][1]=0;
while(!q.empty())
{
x=q.front().x,y=q.front().y;
q.pop();
if(x==m && y==m) continue;//如果是终点就退出(终点的金币花费在终点被推入队列前就dp过了)
for(i=0;i<4;i++)
{
gx=x+fx[i][0], gy=y+fx[i][1];
if(gx<1 || gx>m || gy<1 || gy>m) continue;
if(!col[gx][gy])
{
if(gx==m && gy==m){//特判终点是白色格子的情况,防止终点被跨过
if(dp[gx][gy]>dp[x][y]+2)
dp[gx][gy]=dp[x][y]+2;
continue;
}
for(j=0;j<4;j++)
{
_gx=gx+fx[j][0], _gy=gy+fx[j][1];
if(_gx<1 || _gx>m || _gy<1 || _gy>m) continue;
if(!col[_gx][_gy]) continue;
if(col[_gx][_gy]==col[x][y])
{
if(dp[_gx][_gy]>dp[x][y]+2)
{
dp[_gx][_gy]=dp[x][y]+2;
tmp.x=_gx, tmp.y=_gy;
q.push(tmp);
}
}
else if(dp[_gx][_gy]>dp[x][y]+3){
dp[_gx][_gy]=dp[x][y]+3;
tmp.x=_gx, tmp.y=_gy;
q.push(tmp);
}
}
}
else{
if(col[gx][gy]==col[x][y]){
if(dp[gx][gy]>dp[x][y]){
dp[gx][gy]=dp[x][y];
tmp.x=gx, tmp.y=gy;
q.push(tmp);
}
}
else if(dp[gx][gy]>dp[x][y]+1){
dp[gx][gy]=dp[x][y]+1;
tmp.x=gx, tmp.y=gy;
q.push(tmp);
}
}
}
}
//dfs(1,1,0,0,0);
if(dp[m][m]==inf) printf("-1");
else printf("%d",dp[m][m]);
return 0;
}
(这是改过的代码,考试时没打65-69行。。。也就是判右下角是白色格子的情况)
以上是我想的bfs。
做法2:dfs
当然,这题也可以用dfs……只是我bfs水平比dfs高,dfs那点烂基础只能面壁。
下面是洛谷某dalao的题解:
这是一道四向dfs模板题,于是先打好模板。因为要求最优解,所以dfs过程中碰到墙壁、走到无色区、当前花费大于最优的情况可以直接剪枝,而不要判断是否已经走过,因为已经走过的不一定是最优解。其中,f(i,j) 表示从 (1,1) 走到 (i,j) 的最优解,最后输出 f(m,m)。
本题最难的地方是如何处理这个膜法。我们用一个参数 frog 来表示上次是否已经用过膜法。在使用膜法的时候,因为是dfs,所以我们可以先将要施展膜法的那一格赋为当前所在的格子,保证结果最优,非常容易证明,请大家自行证明,笔者不再过多阐述。然后肯定往新格子上走,这时sum+2。下面一行回溯。
#include <iostream>
#include <cstring>
#include <cmath>
using namespace std;
#define inf 3fffffff
int fx[4] = {-1, 0, 1, 0};
int fy[4] = {0, -1, 0, 1};
int f[110][110];
int mp[110][110];
int m, n, ans = inf;
void dfs(int x, int y, int sum, bool frog) {
if(x < 1 || y < 1 || x > m || y > m) return;
if(!mp[x][y]) return;
if(sum >= f[x][y]) return;
f[x][y] = sum;
if(x == m && y == m) {
if(sum < ans) ans = sum;
return;
}
for(int i = 0; i < 4; ++i) {
int xx = x+fx[i];
int yy = y+fy[i];
if(mp[xx][yy]) {
if(mp[xx][yy] == mp[x][y])
dfs(xx, yy, sum, false);
else dfs(xx, yy, sum+1, false);
} else if(!mp[xx][yy] && !frog) {
mp[xx][yy] = mp[x][y];
dfs(xx, yy, sum+2, true);
mp[xx][yy] = 0;
}
}
}
int main() {
memset(f, 0x7f, sizeof(f));
cin >> m >> n;
for(int i = 1; i <= n; ++i) {
int x, y, c;
cin >> x >> y >> c;
mp[x][y] = c + 1;
}
dfs(1, 1, 0, false);
if(ans == inf) cout << -1;
else cout << ans;
return 0;
}
上面的代码是题解作者写的,但我大致判断dfs有了剪枝后,时间复杂度可能是bfs的很多倍。
我这么说是有考虑的,而且是基于bfs和dfs两者的搜索方法的考虑。我相信OIer都知道两者的搜索方式。bfs是从左上角起点出发,往各个方向都依次、逐层扩展,形成圆式的扩展,也就是说往每个方向走出的步数大致都是相同的。这样可以确保对于所有红/黄格子,根据bfs中的优化(即对于一个格子,大多数情况下后被扩展到的时候金币花费都比原先更大),每格几乎只会往队列中放入一次。但dfs是“冲击式”的,即从左上角起点沿着路径一直走到右下角的终点后,回溯回来时才会逐渐往其它方向尝试,这样会导致“对于一个格子,大多数情况下后被扩展到的时候金币花费都比原先更大”这句话不成立,因为假如一个格子位于偏左上的位置,有可能第一次沿一条路径直接走到终点后,从接近终点的某个位置折回来,在深搜过程中先直达偏左上角的某些格子,而这样到达的花费肯定比从左上角抄近路到达该格子的金币花费大。这就使dfs需要对一个点的金币花费进行许多次更新。很明显,dfs的这一“先到却不优”的特点造成了它的时间开销更大。
不过我仍然特别想炸了臭烘烘的dfs,代码居然这么短……毁我青春
做法3:最短路
我觉得做法1和做法2应该是初中生还好想到的,做法3有点偏题了,但只要绕过弯来就能想到,而且确实能做。
在做法1中已经提到,对于测评数据而言,绝大多数格子通常都是白色的,只有少数的一些红/黄格子会故意连城数条路线。构思出这样一个图,可以想到:把有颜色的格子从1开始依次编号,把能互相到达的点都连上边,边权记录从一点到达另一点所需花费的金币数:如果两点相邻,边的权值就为0(颜色相同)或1(颜色不同),如果两点隔一个白色格子,边的权值就为2(颜色相同)或3(颜色不同)。对边权的赋值 还是用到了我要求读者做这道题之前一定要先搞明白的那个事情,如果你搞明白了那个,边权的赋值也就简单了。
连完边之后,整个棋盘的红/黄格子就形成了一张图。由于最多有m^2个红/黄格子,建的图最多可能有10000个点,因此选用dijkstra、spfa等各种最短路经典算法都可跑出从起点到终点的最短路,而最短路径长度就是最小金币花费(因为边权都是金币花费)。
这段是我自打的,我没写过代码,所以代码就不贴了,有兴趣的可以去别的地方查查或者自己手写。这个方法是我考后自己思考+dalao叙述整出来的。
我的得分:50 (就因为忘了判右下角终点是白色格子的情况了,直接被官方数据卡50分)
4.跳房子
题目描述
跳房子,也叫跳飞机,是一种世界性的儿童游戏,也是中国民间传统的体育游戏之一。
跳房子的游戏规则如下:
在地面上确定一个起点,然后在起点右侧画 n 个格子,这些格子都在同一条直线上。每个格子内有一个数字( 整数),表示到达这个格子能得到的分数。玩家第一次从起点开始向右跳, 跳到起点右侧的一个格子内。第二次再从当前位置继续向右跳,依此类推。规则规定:
玩家每次都必须跳到当前位置右侧的一个格子内。玩家可以在任意时刻结束游戏,获得的分数为曾经到达过的格子中的数字之和。
现在小 R 研发了一款弹跳机器人来参加这个游戏。但是这个机器人有一个非常严重的缺陷,它每次向右弹跳的距离只能为固定的 d。小 R 希望改进他的机器人,如果他花 g 个金币改进他的机器人,那么他的机器人灵活性就能增加 g, 但是需要注意的是,每次弹跳的距离至少为 1。 具体而言, 当g < d时, 他的机器人每次可以选择向右弹跳的距离为 d-g, d-g+1,d-g+2, …, d+g-2, d+g-1, d+g; 否则( 当g ≥ d时),他的机器人每次可以选择向右弹跳的距离为 1, 2, 3, …, d+g-2, d+g-1, d+g。
现在小 R 希望获得至少 k 分,请问他至少要花多少金币来改造他的机器人。
输入输出格式
输入格式:
第一行三个正整数 n, d, k, 分别表示格子的数目, 改进前机器人弹跳的固定距离, 以及希望至少获得的分数。 相邻两个数之间用一个空格隔开。
接下来 n 行,每行两个正整数x_i, s_i,分别表示起点到第i个格子的距离以及第i个格子的分数。 两个数之间用一个空格隔开。 保证x_i按递增顺序输入。
输出格式:
共一行,一个整数,表示至少要花多少金币来改造他的机器人。若无论如何他都无法获得至少 k 分,输出-1。
输入输出样例
说明
输入输出样例 1 说明
花费 2 个金币改进后, 小 R 的机器人依次选择的向右弹跳的距离分别为 2, 3, 5, 3, 4,3, 先后到达的位置分别为 2, 5, 10, 13, 17, 20, 对应 1, 2, 3, 5, 6, 7 这 6 个格子。这些格子中的数字之和 15 即为小 R 获得的分数。
输入输出样例 2 说明
由于样例中 7 个格子组合的最大可能数字之和只有 18 ,无论如何都无法获得 20 分
数据规模与约定
本题共 10 组测试数据,每组数据 10 分。
对于第 1,2 组测试数据, n ≤ 10;
对于第 3,4,5 组测试数据, n ≤ 500;
对于第 6,7,8 组测试数据, d = 1;
对于全部的数据满足1 ≤ n ≤ 500000, 1 ≤ d ≤2000, 1 ≤ x_i, k ≤ 109, |si| < 105。
实话实说,这题是这几年以来的普及组题目中最抽我脸的一题了……
这题我看完第一遍就想到了二分+区间最小值,结果序列的值是随着二分出的弹跳距离而变化的,而我忘了单调队列怎么打了,于是mengbi地使用STL大法狂撸这题(别笑哇,noip2015的普及组t4就可以用STL秒过),最终成功CE(编译错误)。
相信你一定是会这道题的!不会也没关系,你明年再看这道题一定会觉得特别水的~
很明显,弹跳距离远所能包含的弹跳范围 覆盖 弹跳距离近所能包含的弹跳范围,因此对于最小的满足要求的弹跳距离d,大于等于d的弹跳距离也都能满足要求,而小于d的弹跳距离都不能满足要求。
所以首先二分灵活性的增加量g,那接下来就要判断二分出来的g是否能满足要求了。
设f[i]代表跳到第 i 个数时的最大分数,
观察转移方程:f[i] = max(f[j])+ s[i] | x[i]-R<=j<=x[i]-L([L,R]代表灵活性增加g后的弹跳范围)
由于当价格一定时,L和R不变,并且x[i]单调递增,所以满足单调队列优化条件,可以在 $[x[i]-R, x[i]-L]$ 这个滑动窗口中快速取出最大的dp值 $f[j]$。
每次计算出f[i]之后判断其是否大于等于k,若大于等于k则这个灵活性的增加量g满足得分要求。若所有f[i]都小于k,则这个灵活性的增加量g不满足得分要求。
2018.10.3 update:
单调队列优化到底是什么?就是快速去掉一段区间中的不优决策,保证在队列中队头的数是最优决策(本题中队头的最优决策就是最大/最小值)。具体算法知识不属于题解内容,没学过的先学一下吧。
滑动窗口到底是什么?就是一个从序列左端开始,左或右端点都只会往右移动的子区间。由于每次左端点或右端点都要至少往右移动一位,容易发现最多只需要滑动 $2n$ 次端点,因此复杂度是$O(n)$级别的。
#include<iostream>
#include<cstdio>
#include<cmath>
#include<queue>
#define maxn 500001
using namespace std;
inline int read(){
int x=0;bool f=1;char c=getchar();
for(;!isdigit(c);c=getchar()) if(c=='-') f=0;
for(;isdigit(c);c=getchar()) x=(x<<3)+(x<<1)+c-'0';
if(!f) return 0-x;
return x;
}
int n,d,k,x[maxn],s[maxn],dp[maxn];
int head,tail; //monotone queue 单调队列
struct node{
int x,s;
}mq[maxn];
void insert(node a){
while(head<=tail && mq[tail].s <= a.s) tail--;
mq[++tail]=a;
}
bool judge(int xg){
queue<node>q;
head=1,tail=0;
q.push((node){0,0}); //从第0位开始跳
//memset(dp,0,sizeof dp); //可以不做memset
for(int i=1;i<=n;i++){
while(q.size() && q.front().x <= x[i]-d+xg) {insert(q.front()); q.pop();}
while(head<=tail && mq[head].x < x[i]-d-xg) head++; //把太靠前的 一下跳不到的位置删掉。另外这句话不能和上句话写反!因为缓冲区的格子有可能直接跑到前面那段能跳到的区间之前!
if(head>tail) continue; //单调队列为空,说明前面没有格子能跳到当前格子
else dp[i] = mq[head].s + s[i];
if(dp[i]>=k) return 1;
q.push((node){x[i],dp[i]});
}
return 0;
}
int main(){
n=read(),d=read(),k=read();
for(int i=1;i<=n;i++) x[i]=read(),s[i]=read();
int l=0,r=max(d,x[n]-d),mid;
bool ok;
while(l<r){
mid=(l+r)>>1;
if(judge(mid)) r=mid, ok=1;
else l=mid+1;
}
if(!ok) printf("-1\n");
else printf("%d\n",l);
return 0;
}
(好想说这题好水但是木有资格说)
我的得分:0
普及组总得分:250
说白了,不是不会,就是没往细里想。没办法……粗枝大叶就会导致错误。
但想回来,普及组的路程走得确实很艰辛。记得第一次考noip——也就是noip2015普及组,我渣渣得连t3的暴力都打不出来,t4根本就看不懂题,最后以正常发挥的水平只拿了200分的辣鸡成绩,同级的几位dalao们拿了一等奖我却没拿(一等奖分数线240);考noip2016,普及组t3我居然没看懂那个∑(sigma,求和符号)是什么意思,还以为最多能输入10^5 * 3*10^5个数,感觉不会就打了70分暴力,谁知道被那个符号坑了……t4施展STL大法(60分的),结果考场上最后差5分钟就调对了,考后一测直接WA成0分。发挥不好,只拿了270分,从个人的角度拿一等奖已经是侥幸(一等奖分数线245)。
然而考完今年的普及组,我都说不出自己受到了怎样的打击。本来计划AK的结果还是各种被虐Q_Q。虽然北京一等奖分数线才210,我一考完就知道即使炸了也稳拿一等,但把一等奖作为标准已经是我一两年前的追求了。每个OIer在成长过程中,回望过去的目标,会发现它们其实都很菜,就好比这个普及组一等奖,北京分数线210分就是因为全市从第95~201名全都是205分,而总共才6、7百人考,分数线定成205分一等奖人数绝对就超标了。况且,205分是什么概念?t1、t2题水过,t3输出-1得5分,t4没做或输出-1没分(官方t4数据没有一个点的答案是-1,这个坑了众多选手)。这也就是小学组水平的分数。换成我,我6年级考这种普及组都能拿这么多分。只要选手再发挥一下,t3或t4整出个做法再多拿个5分就一等了。像我这样的初三党,还能跟这种水平相比么……可是250分,在分数构成上来看能说明后面的题肯定是会做的,但为什么就拿不全分呢?还是不细致,如前面所说,做题没往细里想,或者说学习基础不扎实。跟自己定的AK目标(400分)差这么远,我也有很多说不出的遗憾。
我也不想再分什么发挥好不好了。考试就是这样,考试结果动不动就会比正常水平大打折扣,而如果想得到好成绩,就必须把自己的目标放高,努力把自己提升到比标准更高的水平,这样才能确保即使发挥不好也能取得好成绩。经历了这么多考试,我觉得这才是重点,也只有努力把自己提升到比标准更高的水平,才能轻松地取得成功;否则,取得成功就要靠考时的赌博——赌博自己会的都能做、做的都能对。
所以,别把自己放在标准的位置,要把自己放得比标准更高一些。noip的一等奖也是如此,我考提高组差不多就是这样的经历(但我哪敢自称我为了目标付出了很多努力,不然我学了这么多年OI怎么还是个沙茶)
正好我接下来也要说提高组的经历。
提高组
今年是我加入OI以来第一次考提高组。其实我之前对提高组是很过敏的,因为大家都知道,去年——noip2016的d1t2坑炸了全国选手。对你没看错,就是那道可恶的天天爱跑步。
还有noip2012的d1t2 国王游戏 这类题,也搞得我心神不宁的。(那是noip最后一道考高精度的题,同行们早都说再也不会有国王游戏这种题了)
然而,今年一考过提高组,我才发现提高组也没有想象中的那么碾人。但结果也不怎么让我满意。
在回顾考试之前先回顾一下复习情况:
考前我把各个noip板块都复习了,比如说LCA(来自天天爱跑步)、倍增(来自货车运输)、数论(来自组合数问题)、动态规划(来自斗地主、子串、换教室等众多noip题目)等前几年的noip考点。其中动态规划是前几年非常爱考的考点,noip2015有两三道题都要用到这个可啪的知识(众所周知动规是最不好学也是最没法学的算法)。此外,我还复习了最短路、强连通分量、树链剖分、线段树、差分、字符串哈希、后缀数组(后来才TM知道好像并不考这玩意)等中端算法或模板,它们在前几年考的好像不多。
还有一个最不用学的,但也是最复杂的知识点——搜索。别看这玩意简单,不练还真不行,而且写搜索最好要有面向对象编程的习惯(很多算法之外的游戏、APP等程序大多都是面向对象的做法,即把各个操作尽量封装成函数,然后在需要时调用或接上函数,等等),我的经验告诉我这样有助于调试结构复杂的搜索程序。搜索在noip中也有经典例题,比如靶形数独和Mayan游戏。靶形数独是noip2009提高组的t4(提高组在2011年以前跟普及组都是每年都只考半天,4道题,所以t4在当时就是最后一题。2011年起正式分成两天,每天考3道题,总题数加成6道),Mayan游戏是noip2011提高组的d1t3。一看就知道都放在了最后一题,可想而知搜索是万不可忽略的一个难点。(但今年并没考搜索)
另外,考后我才意识到自己应该复习一下并查集。那东西也不是不用复习……
说了这么多,该讲讲题目和我做的情况了。
1.小凯的疑惑
问题描述
小凯手中有两种面值的金币,两种面值均为正整数且彼此互素。每种金币小凯都有无数个。在不找零的情况下,仅凭这两种金币,有些物品他是无法准确支付的。现在小凯想知道在无法准确支付的物品中,最贵的价值是多少金币?注意:输入数据保证存在小凯无法准确支付的商品。
输入格式
输入文件名为math.in。
输入数据仅一行,包含两个正整数 a 和 b,它们之间用一个空格隔开,表示小凯手中金币的面值。
输出格式
输出文件名为math.out。
输出文件仅一行,一个正整数 N,表示不找零的情况下,小凯用手中的金币不能准确支付的最贵的物品的价值。
输入样例#1:
3 7
输出样例#1:
11
输入输出样例1说明
小凯手中有面值为3和7的金币无数个,在不找零的前提下无法准确支付价值为 1、2、4、5、8、11 的物品,其中最贵的物品价值为 11,比 11 贵的物品都能买到,比如:
12=3×4+7×0
13=3×2+7×1
14=3×0+7×2
15=3×5+7×0
……
数据规模与约定
对于 30%的数据: 1<=a,b<=50。
对于 60%的数据: 1<=a,b<=10,000。
对于 100%的数据:1<=a,b<=1,000,000,000。
今年的d1t1题居然是数竞题-_-我的很多战友(从初一到高二皆有)没找出这题的规律,从而只打了60分的暴力。当然也有不少30、50分的…… 按照正确率来看,这道题有点超纲了,坑掉了许多计算机神犇。
我在考场上一开始想到了exgcd(扩展欧几里得,简称扩欧),即用解ax+by=c的方法来做。但无奈思路卡壳。于是我手试了几组数据的答案,结果“手算出奇迹”了。我也因此成为了我们这里少数几个AC d1t1的选手中的一个。
我在草稿纸上列了几组比较小的数据:
于是我就发现a*(-1)+b*(a-1)总是最大答案-_-……考试的时候不到半小时就发现了这个规律,于是我干脆直接把这个公式敲上去了,也不管对不对(急着做后面的题),反正扩欧的做法我是mengmengbibi的。(谁知道这么个小玩意就拿了100分……)
这题的思路应该说本身就可以这么找。接下来我会提到2种做法、3种解释,每种解释都值得一看。我就率先用保证大家都能理解的方法形象地解释一下辣。
做法1:公式法
下图为a=8,b=3的例子,易得最大的拼不出的数是13(8*(-1)+3*(8-1))。用有颜色的竖条覆盖的数是能用8和3能拼出来的。
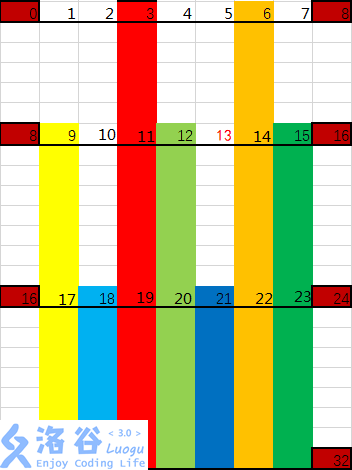
为了方便理解,我从小的数(3)开始推起(其实先推8也可以,只不过图要长很多很多)。不难发现,3、6、9、12、15等数都是3的倍数,因此它们都能直接(用3)拼出来。而图标中每行放了8个数(每行第一个数是补全用的,等于上一行最后一个数,因此不算),同一竖列中相邻两个数都差8,所以与这些数在同一竖列且在这些数下面的数也都能拼出来(先用3拼出3、6、9、12、15这些数,然后再累加若干个8即得到)。我们可以形象地表示一下,也就是在图中以这些3的倍数为顶,往下涂竖线,那么竖线所涂到的数都能被拼出来。这样涂出来后,你就会发现神奇的东西(群众:MMP考试的时候能想到就好了)。
画这个图像按照这个顺序涂:以3为顶涂竖线,然后以6为顶涂竖线...一直到以21为顶涂竖线。此时一共涂了7条竖线,即8-1(a-1)。看上面的图也就涂到这里了。细心的人会发现,21所在的这一行已经被涂满了,但我们不是只往下涂了7条竖线吗?第8条竖线不涂么?很简单啊,因为24是3和8的最小公倍数。做到这里,大家应该知道为什么要一行放8个数了吧!这张图最右边的一列就是给8的倍数准备的。也就是说,第8列本来就都能用8直接拼出来,它们相当于一开始就默认都是褐色(如图),也就不用再为3给它们涂色了。
通过上面的说法,还有一个问题就解决了,那就是为什么这7条竖线互不重叠。因为题目说了两个数互质辣。那为什么互质就互不重叠了?这就是思考题了。因为3和8作为一对互质的数是没有公共因子的,即对于它们的最小公倍数24,任何全由3拼成的小于24的数一定不等于任何全由8拼成的小于24的数。转化一下可得任何一个小于24的数都不能被3和8用两种或更多方法拼出来。这种问题应该找dalao学习一下,我不是dalao,所以只能点到为止了。
这样一来,涂到21的时候,总共涂了7条竖线,且竖线是依次以3、6、9等3的倍数为顶的。此时整张图已经有了8条带颜色的竖线,也就是说涂完21后,从当前行开始往下的所有数都被竖线涂到过了,它们都能被拼出来。而21又是最后一个(最大的一个)成为竖线顶的数,它上面的那个数就是最大的拼不出来的数(核心!)看图,它上面的数是13,是不是就是最大的拼不出的那个数?(用红色标出了)
所以这个尬式是这么推出来的……这也警醒各位OIer一定要有数学中代数和几何的综合思维能力啊……
整合一下公式:a=8,b=3,那么最后一个成为竖线顶的数就是3*(8-1)=21(前面已经说明),即b*(a-1)。它上面的那个数就是21-8=13,即ans=b*(a-1)-a。
那些(a-1)*(b-1)-1、ab-a-b什么的答案,其实只是把b*(a-1)-a重新组合了一下……所以都是对的。
#include<iostream>
#include<cstdio>
using namespace std;
inline int read(){
int x=0; bool f=1; char c=getchar();
while(!isdigit(c)){if(c=='-') f=0; c=getchar();}
while(isdigit(c)){x=x*10+c-'0'; c=getchar();}
if(!f) return 0-x;
return x;
}
long long a,b;
int main(){
a=read(),b=read();
if(a<b) swap(a,b);
printf("%lld",b*(a-1)-a);
return 0;
}
2018.3.9 update:if(a<b) swap(a,b); 这句考后才发现可以不要,只是画图的时候让a>b会好理解一些。
2018.10.8 update:
然后就有人D我:这跟找规律一样啊,哪有数学解释?
好吧,那这里补点数学解释。
前文说过,前7条竖线是互不重叠的,而第8列(所有8的倍数)已经默认有一条竖线(因为我们是以8的倍数为行基准,8的倍数都在同一列上,可预处理),所以当涂完7条竖线后(到24-3=21),从这一行开始,以下所有行都一定被涂满了。
所以排除了第3行及以后的数成为答案的可能性,再排除第2行最后一列的数成为答案的可能性(最后一列是8的倍数),最大的可能答案变为(3-1)*8-1=15。
那怎么判断当前的最大可能答案是否就是答案呢?
把15加8,得到23,我们发现23不是一条竖线的起点,结合前面说过的结论“任何一个小于24的数都不能被3和8用两种或更多方法拼出来”,可得$23=3x+8y$ | $x>0,y>0$,去掉一个8后至少满足$15=3x+8y$ | $x>0,y\ge 0$。也就是说15能被拼出来,所以最大可能答案减1。
把14加8,得到22,也不是一条竖线的起点,思路同上,最大答案再减1。
我们又希望答案最大,所以答案实际上就是向前找到的第一个加上8后是某条竖线的起点的数。由于初始最大可能答案为最后一条竖线的起点的上一行的最右端(当然排除8的倍数那一列,是右数第二个),所以一定可以从大到小遍历到最后一条竖线的起点的上面那个数,那么它就是答案。
而最后一条竖线的起点与下一个8的倍数只差3,下一个8的倍数又是3和8的最小公倍数3*8,所以答案就是3*8-3-8=13。
改为设数证明,通解就是$ans=a*b-a-b$。
当然,以下还有dalao的解释:
不妨设 $a < b$
假设答案为 $x$
若 $x \equiv ma \pmod b (1 \leq m \leq b - 1)$
即 $x = ma + nb (1 \leq m \leq b - 1)$
显然当 $n \geq 0$ 时 $x$ 可以用 $a, b$ 表示出来,不合题意。
因此当 $n = -1$ 时 $x$ 取得最大值,此时 $x = ma - b$。
显然当 $m$ 取得最大值 $b - 1$ 时 $x$ 最大,此时 $x = (b - 1)a - b = ab - a - b$。
因此 $a, b$ 所表示不出的最大的数是 $ab - a - b$。
做法2:扩欧
我这种数学菜鸡怎么可能会把扩欧搞出来,于是我继续看看dalao是怎么搞的。
·大家如果有不懂的,可以发评论,有机会可以交流交流。
我的得分:100
2.时间复杂度
题目描述
小明正在学习一种新的编程语言 A++,刚学会循环语句的他激动地写了好多程序并 给出了他自己算出的时间复杂度,可他的编程老师实在不想一个一个检查小明的程序, 于是你的机会来啦!下面请你编写程序来判断小明对他的每个程序给出的时间复杂度是否正确。
A++语言的循环结构如下:
F i x y
循环体
E
其中F i x y表示新建变量 i(变量 i 不可与未被销毁的变量重名)并初始化为 x, 然后判断 i 和 y 的大小关系,若 i 小于等于 y 则进入循环,否则不进入。每次循环结束后 i 都会被修改成 i+1,一旦 i 大于 y 终止循环。
x 和 y 可以是正整数(x 和 y 的大小关系不定)或变量 n。n 是一个表示数据规模的变量,在时间复杂度计算中需保留该变量而不能将其视为常数,该数远大于 100。
“E”表示循环体结束。循环体结束时,这个循环体新建的变量也被销毁。
注:本题中为了书写方便,在描述复杂度时,使用大写英文字母“O”表示通常意义下“Θ”的概念。
输入输出格式
输入格式:
输入文件第一行一个正整数 t,表示有 t(t≤10)个程序需要计算时间复杂度。 每个程序我们只需抽取其中 F i x y和E即可计算时间复杂度。注意:循环结构 允许嵌套。
接下来每个程序的第一行包含一个正整数 L 和一个字符串,L 代表程序行数,字符串表示这个程序的复杂度,O(1)表示常数复杂度,O(n^w)表示复杂度为n^w,其中w是一个小于100的正整数(输入中不包含引号),输入保证复杂度只有O(1)和O(n^w) 两种类型。
接下来 LL 行代表程序中循环结构中的F i x y或者 E。 程序行若以F开头,表示进入一个循环,之后有空格分离的三个字符(串)i x y, 其中 ii 是一个小写字母(保证不为n),表示新建的变量名,x 和 y 可能是正整数或 n ,已知若为正整数则一定小于 100。
程序行若以E开头,则表示循环体结束。
输出格式:
输出文件共 t 行,对应输入的 t 个程序,每行输出Yes或No或者ERR(输出中不包含引号),若程序实际复杂度与输入给出的复杂度一致则输出Yes,不一致则输出No,若程序有语法错误(其中语法错误只有: ① F 和 E 不匹配 ②新建的变量与已经存在但未被销毁的变量重复两种情况),则输出ERR 。
注意:即使在程序不会执行的循环体中出现了语法错误也会编译错误,要输出 ERR。
输入输出样例
输入样例#1:
8
2 O(1)
F i 1 1
E
2 O(n^1)
F x 1 n
E
1 O(1)
F x 1 n
4 O(n^2)
F x 5 n
F y 10 n
E
E
4 O(n^2)
F x 9 n
E
F y 2 n
E
4 O(n^1)
F x 9 n
F y n 4
E
E
4 O(1)
F y n 4
F x 9 n
E
E
4 O(n^2)
F x 1 n
F x 1 10
E
E
输出样例#1:
Yes
Yes
ERR
Yes
No
Yes
Yes
ERR
说明
【输入输出样例解释1】
第一个程序 i 从 1 到 1 是常数复杂度。
第二个程序 x 从 1 到 n 是 n 的一次方的复杂度。
第三个程序有一个 F 开启循环却没有 E 结束,语法错误。
第四个程序二重循环,n 的平方的复杂度。
第五个程序两个一重循环,n 的一次方的复杂度。
第六个程序第一重循环正常,但第二重循环开始即终止(因为n远大于100,100大于4)。
第七个程序第一重循环无法进入,故为常数复杂度。
第八个程序第二重循环中的变量 x 与第一重循环中的变量重复,出现语法错误②,输出 ERR。
【数据规模与约定】
对于 30%的数据:不存在语法错误,数据保证小明给出的每个程序的前 L/2 行一定为以 F 开头的语句,第 L/2+1 行至第 L 行一定为以 E 开头的语句,L≤10,若 x、y 均为整数,x 一定小于 y,且只有 y 有可能为 n。
对于 50%的数据:不存在语法错误,L≤100,且若 x、y 均为整数,x 一定小于 y, 且只有 y 有可能为 n。
对于 70%的数据:不存在语法错误,L≤100。
对于 100%的数据:L≤100。
我考试前第一次浏览题目的时候,发现今年的d1t2居然这么水,是道模拟题,跟去年的d1t2(天天爱跑步)比,思维难度完全不在一个等级QwQ。
其实更准确地说法应该是这题想考察选手的代码能力。也就是说,不光要会算法,成为数学大佬,还要有程序员的意识。
但我还是没明白部分分是干嘛用的,估计是给不会用栈的人一点暴力分吧……
把题目内容分解,先搞清大体遍历思路,然后再具体到每一个细节,包括判断时间复杂度大小、检查语法错误,等等。做这道题前就应该把思路弄顺了,不然思路甚至程序最后可能会变得槽杂难懂。
我在考场上就按照我习惯的做法,边输入一行边处理了。
1.记录每层循环用到的变量,判断内层循环的变量在外层有没有用过;
2.记录每层循环的信息,方便回溯回来后按照循环信息把答案还原回去;
3.对于F打头的行(循环开始行),根据x、y的情况(共有4种,程序里会有详述)计算该层复杂度;
4.对于E打头的行,把当前层循环所更改的答案改回去,并退出当前层循环。我用了一个栈模拟进入的循环层。
5.对于第3条,当x>y时,该层循环实际上是进不去的,那么该层里面的那些循环也进不了,但里面的循环内容还要照常输入。因此用一个变量(我用的o1)记录当前循环层的深度,那么之后输入的位于该层循环里面的循环只需要判断变量名是否与外层循环的重复(这种情况题目没说清楚),然后过掉就完了。等回溯到退出该层循环时去掉这个变量标记(o1)就好了。
#include<iostream>
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<stack>
#define inf 2147483647
using namespace std;
inline int read(){
int x=0; bool f=1; char c=getchar();
while(!isdigit(c)){if(c=='-') f=0; c=getchar();}
while(isdigit(c)){x=x*10+c-'0'; c=getchar();}
if(!f) return 0-x;
return x;
}
int T,L,len,deep,cf,intx,inty,o1=inf;//o1用来记录类似于n 1这样的进不去的循环的深度,它里面(比它更深)的循环内容输入完、记录变量后直接跳过,不算复杂度。等回溯回来时再撤掉o1记录。
//deep和s.size()的意义是一样的,都表示在第几层循环
long long ans,ljcf;//ljcf(累计次方)表示到达当前位置时的时间复杂度为O(n^ljcf)
char c[10],F,I,X[10],Y[10];
bool usedbl[128],deepn[101],CE;//usedbl(used变量)记录变量名称是否使用过,deepn记录哪些循环层的复杂度大于O(1)(回溯的时候需要去掉这些层的复杂度),CE(compile error)用来记录是否编译错误
stack<char> s;//存储当前位置在哪些循环之中
int main(){
int i,j;
T=read();
while(T--){
//初始化
CE=deep=0;ans=ljcf=0;
o1=inf;//一开始没有进不去的循环
while(!s.empty()) s.pop();
memset(usedbl,0,sizeof(usedbl));
memset(deepn,0,sizeof(deepn));
L=read();
scanf("%s",c);
if(c[2]=='1') cf=0;//时间复杂度是O(1)
else{//时间复杂度是O(n^w)
cf=c[4]-'0';//读取w,即复杂度值
if(isdigit(c[5])) cf=cf*10+c[5]-'0';//题中说了w小于100,所以w可能是两位数。所以要判断w是不是两位数
}
/*
//我采用了边读入边直接处理的做法,只要把循环层累放入栈,回溯时删除栈顶的循环层就可以判断循环是否合法了。
其实常规思路应该是全输入完后从头尾两端往里夹着算复杂度。
*/
for(i=0;i<L;i++){
cin>>F;//考场上用scanf输入字符串炸了,于是只好全程cin
//cout<<i<<' '<<deep<<' '<<s.size()<<' '<<o1<<' '<<CE<<'\n';
if(F=='E'){//退出一层循环。建议先看58行起的进入循环的内容
if(s.empty() || deep<=0){CE=1;continue;}//E的数量超过F的数量(即在0层循环时还要退),那就编译错误了
//否则是合法退循环
if(deepn[deep]){deepn[deep]=0; ljcf--;}//如果这一层的时间复杂度为O(n),在退出这一层循环时就要减去它的复杂度
if(deep==o1) o1=inf;//这一层循环是进不去的,那么退掉这层循环之后就要清掉o1变量以确保能进入后面的循环
deep--;//循环深度-1
usedbl[s.top()]=0;//将这个变量设为未使用
s.pop();//弹掉循环层
continue;
}
cin>>I>>X>>Y;
if(CE) continue;//已经编译错误了,该程序中后面的内容输入完后就不用再管了
deep++;//循环深度+1
if(usedbl[I-'a']){CE=1; continue;}//如果变量名被使用过,就记录编译错误,但后面输入的程序内容依然是要输入的,所以不能直接退循环
usedbl[I-'a']=1;//记录变量已使用过
s.push(I-'a');//记录当前循环层(的变量名)
if(deep>=o1) continue;//如果循环是进不去的 ,那记录完循环变量信息后就直接过掉
//能到这里说明能正常到达该层,那么该层的复杂度需要算
if(X[0]=='n' && Y[0]=='n') continue;//X=Y=n,相当于O(1),直接过
else if(X[0]=='n'){o1=deep; continue;}//X=n>100, Y<100,相当于进不去,记录o1变量,也过
else if(Y[0]=='n') ljcf++,deepn[deep]=1;//X<100,y=n>100,相当于O(n)(因为n远大于100,从小于100的数到远大于100的n接近需要O(n)的时间),时间复杂度垒上一个n,这一层做复杂度大于O(1)的标记
else{
intx=atoi(X),inty=atoi(Y);//把X和Y转成整数,方便判断大小(不要拿字符串直接比!)
if(intx>inty) o1=deep;//X>Y,相当于进不去,记录o1变量,直接过
//否则两个常数的复杂度相当于O(1),直接过
continue;
}
ans=max(ljcf,ans);//对于刚才的第三种情况,复杂度(ljcf)增加了,需要更新最大的时间复杂度
//cout<<"deep:"<<deep<<" ljcf:"<<ljcf<<'\n';
}
//cout<<ans<<' '<<cf<<'\n';
if(CE || !s.empty()){printf("ERR\n"); continue;}//编译错误或者还有循环层没有退出。(!s.empty()可替换为deep>0)
if(ans==cf) printf("Yes\n");//判断最大时间复杂度是否跟预期相同
else printf("No\n");
}
return 0;
}
缕清了思路,是不是就好做了?
但是我考试时把Yes和No的大小写写错了(Yes->YES No->NO),而且考试的时候由于没有使用对拍,肉眼对样例结果时硬是没发现。结果这题白写对了,直接被坑掉100分T_T
所以说,仔细检查还是很重要啊!下次还得注意一下字母大小写的问题,这次就当是一回教训吧。。。
我的得分:0
3.逛公园
题目描述
策策同学特别喜欢逛公园。公园可以看成一张N个点M条边构成的有向图,且没有 自环和重边。其中1号点是公园的入口,N号点是公园的出口,每条边有一个非负权值, 代表策策经过这条边所要花的时间。
策策每天都会去逛公园,他总是从1号点进去,从N号点出来。
策策喜欢新鲜的事物,它不希望有两天逛公园的路线完全一样,同时策策还是一个特别热爱学习的好孩子,它不希望每天在逛公园这件事上花费太多的时间。如果1号点到N号点的最短路长为d,那么策策只会喜欢长度不超过d+K的路线。
策策同学想知道总共有多少条满足条件的路线,你能帮帮它吗?
为避免输出过大,答案对P取模。
如果有无穷多条合法的路线,请输出−1。
输入输出格式
输入格式:
第一行包含一个整数 T, 代表数据组数。
接下来T组数据,对于每组数据: 第一行包含四个整数 N,M,K,P,每两个整数之间用一个空格隔开。
接下来M行,每行三个整数ai,bi,ci,代表编号为ai,bi的点之间有一条权值为ci的有向边,每两个整数之间用一个空格隔开。
输出格式:
输出文件包含 T 行,每行一个整数代表答案。
输入输出样例
输入样例#1:
2
5 7 2 10
1 2 1
2 4 0
4 5 2
2 3 2
3 4 1
3 5 2
1 5 3
2 2 0 10
1 2 0
2 1 0
输出样例#1:
3
-1
说明
【样例解释1】
对于第一组数据,最短路为3。1 – 5,1 – 2 – 4 – 5,1 – 2 – 3 – 5 为 3 条合法路径。
【测试数据与约定】
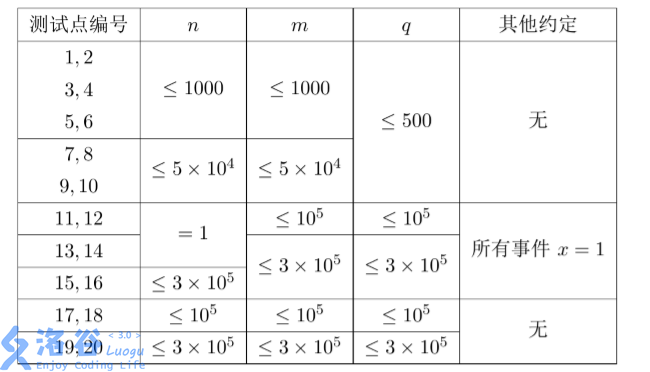
对于不同的测试点,我们约定各种参数的规模不会超过如下
| 测试点编号 | T | N | M | K | 是否有0边 |
|---|---|---|---|---|---|
| 1 | 5 | 5 | 10 | 0 | 否 |
| 2 | 5 | 1000 | 2000 | 0 | 否 |
| 3 | 5 | 1000 | 2000 | 50 | 否 |
| 4 | 5 | 1000 | 2000 | 50 | 否 |
| 5 | 5 | 1000 | 2000 | 50 | 否 |
| 6 | 5 | 1000 | 2000 | 50 | 是 |
| 7 | 5 | 100000 | 200000 | 0 | 否 |
| 8 | 3 | 100000 | 200000 | 50 | 否 |
| 9 | 3 | 100000 | 200000 | 50 | 是 |
| 10 | 3 | 100000 | 200000 | 50 | 是 |
对于100%的数据,1≤P≤109,1≤ai,bi≤N,0≤ci≤1000。
数据保证:至少存在一条合法的路线。
由于我把t2从9点搞到11点(我调程序就麻烦没办法),我看完这道题之后发现只剩下50分钟了,于是抓紧打了个SPFA+DFS的暴力(即先算出最短路长d,再dfs所有长度不超过d+K的路径)。反正时间不够了,我也没想着拿满分。
出了考场之后听说这个方法能拿60分,因为SPFA的O(nlogm)(注:SPFA的复杂度准确地说其实是玄学,学过的dalao应该知道)复杂度肯定能轻松跑过,关键是dfs,就得看n的大小了。其他选手都吵吵着说n=1000的数据可以用SPFA跑过,结果都TLE了。最后我只过了所有K=0的点(测试点1、2、7)(这不是废话么,K=0的时候只需要SPFA求个最短路了,剪枝的dfs都不怎么跑)。
我的想法也就是这样了……
下面是幻想正解:
如果你在考场上还有足够时间做这题(个人觉得最少1.5h),是否很容易就发现day1的dp好像没了?
所以这估计就是一道dp题了。这题的正解跟往年套路一样,noip2015的d1t3(斗地主)、noip2016的d1t3(换教室)等题目都是大dp,而且状态也奇多无比,找到入手点还不够烧脑子。看到这道题时,你只要注意一下K<=50就大概能想到这是一个与k有关的DP了。
题意:求dis(1,n)<=dis(1,n)+k 的路径数
设f[u][k]表示比 dis(1,u) 长度多 k 的路径数,则
dp[v][k] = ∑dp[u][k+ dis[u]+w-dis[v]] ((u,v)∈E) //dis[i]表示从起点到点i的最短距离,w是(u,v)边权
但如果朴素地从起点开始dp,容易走进某些到不了终点的死胡同。所以可以从终点反过来搜,优化时间。
特别地,如果一个零环位于一条从1到n长度<=d+K的路径上,则无解,输出-1即可。
还有一种方法是 将原图拓扑排序后根据拓扑序进行dp。(去 luogu 之类的地方看看?)
#include<bits/stdc++.h>
#define MAXN 100001
#define MAXM 200001
using namespace std;
inline int read(){
int x=0;bool f=1;char c=getchar();
for(;!isdigit(c);c=getchar()) if(c=='-') f=0;
for(;isdigit(c);c=getchar()) x=x*10+c-'0';
if(!f) return 0-x;
return x;
}
struct Edge{
int u, v, w, next;
}e[MAXM];
int n, m, k, head[MAXN], p, d[MAXN], f[MAXN][55], b[MAXN][55], ans;
bool vis[MAXN], flag; //flag在记忆化搜索时用,flag=1表示有零环,即应输出-1
void spfa() {
queue<int> q;
d[1] = 0;
q.push(1);
int i,u;
while (!q.empty()) {
u = q.front(); q.pop();
vis[u] = 0;
for (i = head[u]; i; i = e[i].next) {
if (d[e[i].v] > e[i].w+d[u]) { //更新最短距离
d[e[i].v] = d[u]+e[i].w;
if (!vis[e[i].v]) { //目标点不在队列里,就将它加入队列
vis[e[i].v] = 1;
q.push(e[i].v);
}
}
}
}
}
int dfs(int u, int step) {
if (b[u][step] == 1 || flag) return flag = 1; //如果有零环就退出。这里能这么判零环是因为刚刚已经以dis(1,u)+step的距离到过这个点而还没退回去,现在却又以dis(1,u)+step的距离到这个点,说明走了一遍零环。于是就可以判了
if (b[u][step] == 2) return f[u][step]; //剪枝,如果一个点曾经到过(注意是曾经,表示它不在当前路径上),就直接返回它的答案
b[u][step] = 1; //设置该点正在路径上
for (int i = head[u], w; i; i = e[i].next) {
w = step+ d[u]-d[e[i].v]-e[i].w; //注意由于图是反向的,这里的有向边(u,v)在原图中实际上是(v,u),因此dis[u]=dis[v]+w,e[i].w也就跟d[e[i].v]同号了
if (w > k || w < 0) continue;
f[u][step] += dfs(e[i].v, w);
f[u][step] %= p;
}
b[u][step] = 2; //设置该点曾经访问过
return f[u][step]; //回溯答案
}
int main() {
int T = read(), i;
while (T--) {
memset(head, 0, sizeof(head));
n = read(), m = read(), k = read(), p = read();
for (i = 1; i <= m; i++) {
e[i].u = read(), e[i].v = read(), e[i].w = read();
e[i].next = head[e[i].u];
head[e[i].u] = i;
}
memset(vis, 0, sizeof(vis));
memset(d, 127, sizeof(d));
spfa();
memset(head, 0, sizeof(head));
for (i = 1; i <= m; i++) { //将图反向连接,dfs要从终点出发
swap(e[i].u, e[i].v);
e[i].next = head[e[i].u];
head[e[i].u] = i;
}
memset(f, 0, sizeof(f));
memset(b, 0, sizeof(b));
f[1][0] = 1;
ans = 0, flag = 0;
for (i = 0; i <= k; i++) { //枚举与最短路径的差
ans += dfs(n, i); //因为dfs是回溯,所以要从终点先往起点延伸路径,然后把答案回溯回终点
ans %= p;
}
printf("%d\n", flag ? -1 : ans);
}
return 0;
}
我的得分:30
第一天出考场后我该怎么说呢,激动又轻松。当然,我当时并不知道t2打错了大小写,t3也只能拿30分而不是60分。考试过了好几天我才发现第一天的分整整少了一半。
4.奶酪
题目描述
现有一块大奶酪,它的高度为 h,它的长度和宽度我们可以认为是无限大的,奶酪 中间有许多 半径相同 的球形空洞。我们可以在这块奶酪中建立空间坐标系,在坐标系中, 奶酪的下表面为z=0,奶酪的上表面为z=h。
现在,奶酪的下表面有一只小老鼠 Jerry,它知道奶酪中所有空洞的球心所在的坐 标。如果两个空洞相切或是相交,则 Jerry 可以从其中一个空洞跑到另一个空洞,特别 地,如果一个空洞与下表面相切或是相交,Jerry 则可以从奶酪下表面跑进空洞;如果 一个空洞与上表面相切或是相交,Jerry 则可以从空洞跑到奶酪上表面。
位于奶酪下表面的 Jerry 想知道,在 不破坏奶酪 的情况下,能否利用已有的空洞跑 到奶酪的上表面去?
空间内两点 P1(x1,y1,z1)、P2(x2,y2,z2)的距离公式如下:
输入输出格式
输入格式:
每个输入文件包含多组数据。
输入文件的第一行,包含一个正整数 T,代表该输入文件中所含的数据组数。
接下来是 T 组数据,每组数据的格式如下: 第一行包含三个正整数 n,h 和 r,两个数之间以一个空格分开,分别代表奶酪中空洞的数量,奶酪的高度和空洞的半径。
接下来的 n 行,每行包含三个整数 x,y,z,两个数之间以一个空格分开,表示空洞球心坐标为(x,y,z)。
输出格式:
输出文件包含 T 行,分别对应 T 组数据的答案,如果在第 i 组数据中,Jerry 能从下表面跑到上表面,则输出Yes,如果不能,则输出No (均不包含引号)。
输入输出样例
输入样例#1:
3
2 4 1
0 0 1
0 0 3
2 5 1
0 0 1
0 0 4
2 5 2
0 0 2
2 0 4
输出样例#1:
Yes
No
Yes
说明
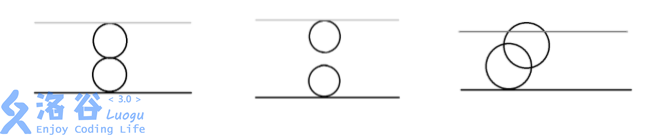
【输入输出样例 1 说明】
第一组数据,由奶酪的剖面图可见:
第一个空洞在(0,0,0)与下表面相切
第二个空洞在(0,0,4)与上表面相切 两个空洞在(0,0,2)相切
输出 Yes
第二组数据,由奶酪的剖面图可见:
两个空洞既不相交也不相切
输出 No
第三组数据,由奶酪的剖面图可见:
两个空洞相交 且与上下表面相切或相交
输出 Yes
【数据规模与约定】
对于 20%的数据,n=1,1≤h,r≤10,000,坐标的绝对值不超过 10,000。
对于 40%的数据,1≤n≤8, 1≤h ,r≤10,000,坐标的绝对值不超过 10,000。
对于 80%的数据, 1≤n≤1,000, 1≤h,r≤10,000,坐标的绝对值不超过10,000。
对于 100%的数据,1≤n≤1,000,1≤h,r≤1,000,000,000,T≤20,坐标的 绝对值不超过 1,000,000,000。
这题其实坑处挺多的,不过很明显就是暴力纯搞。(考场上半小时解决?)
方法1:并查集
方法2:搜索
#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstring>
using namespace std;
inline long long read(){
long long x=0; bool f=1; char c=getchar();
while(!isdigit(c)){if(c=='-') f=0; c=getchar();}
while(isdigit(c)){x=x*10+c-'0'; c=getchar();}
if(!f) return 0-x;
return x;
}
struct cheese{
long long x,y,z;
}c[1001];
struct edge{
int to,next;
}e[(1001*1001)<<1];
int head[1001];
bool vis[1001];
int T,n,cnt;
long long c_h,r;
bool calc(long long x1,long long y1,long long z1,long long x2,long long y2,long long z2){
if(sqrt((x1-x2)*(x1-x2)+(y1-y2)*(y1-y2)+(z1-z2)*(z1-z2))<=2*r) return 1;
else return 0;
}
inline void add(int x,int y){
e[++cnt].to=y;
e[cnt].next=head[x];
head[x]=cnt;
}
bool up,down;
bool dfs(int u){
vis[u]=1;
if(c[u].z-r<=0 && c[u].z+r>=0) down=1;
if(c[u].z+r>=c_h && c[u].z-r<=c_h) up=1;
if(up && down) return 1;
for(int i=head[u];i;i=e[i].next){
if(vis[e[i].to]) continue;
if(dfs(e[i].to)) return 1;
}
return 0;
}
int main(){
int i,j;
bool ok;
T=read();
while(T--){
memset(head,0,sizeof(head));
memset(vis,0,sizeof(vis));
cnt=0; ok=0;
n=read(),c_h=read(),r=read();
for(i=1;i<=n;i++) c[i].x=read(),c[i].y=read(),c[i].z=read();
for(i=1;i<n;i++)
for(j=i+1;j<=n;j++)
if(calc(c[i].x,c[i].y,c[i].z,c[j].x,c[j].y,c[j].z)) add(i,j),add(j,i);
for(i=1;i<=n;i++){
if(vis[i]) continue;
up=down=0;
if(dfs(i)){printf("Yes\n");ok=1;break;}
}
if(!ok) printf("No\n");
}
return 0;
}
我的得分:100
5.宝藏
题目描述
参与考古挖掘的小明得到了一份藏宝图,藏宝图上标出了 n 个深埋在地下的宝藏屋, 也给出了这 n 个宝藏屋之间可供开发的 m 条道路和它们的长度。
小明决心亲自前往挖掘所有宝藏屋中的宝藏。但是,每个宝藏屋距离地面都很远, 也就是说,从地面打通一条到某个宝藏屋的道路是很困难的,而开发宝藏屋之间的道路 则相对容易很多。
小明的决心感动了考古挖掘的赞助商,赞助商决定免费赞助他打通一条从地面到某 个宝藏屋的通道,通往哪个宝藏屋则由小明来决定。
在此基础上,小明还需要考虑如何开凿宝藏屋之间的道路。已经开凿出的道路可以 任意通行不消耗代价。每开凿出一条新道路,小明就会与考古队一起挖掘出由该条道路 所能到达的宝藏屋的宝藏。另外,小明不想开发无用道路,即两个已经被挖掘过的宝藏屋之间的道路无需再开发。
新开发一条道路的代价是:L×K
L代表这条道路的长度,K代表从赞助商帮你打通的宝藏屋到这条道路起点的宝藏屋所经过的 宝藏屋的数量(包括赞助商帮你打通的宝藏屋和这条道路起点的宝藏屋) 。
请你编写程序为小明选定由赞助商打通的宝藏屋和之后开凿的道路,使得工程总代价最小,并输出这个最小值。
输入输出格式
输入格式:
第一行两个用空格分离的正整数 n 和 m,代表宝藏屋的个数和道路数。
接下来 m 行,每行三个用空格分离的正整数,分别是由一条道路连接的两个宝藏 屋的编号(编号为 1~n),和这条道路的长度 v。
输出格式:
输出共一行,一个正整数,表示最小的总代价。
输入输出样例
输入样例#1:
4 5
1 2 1
1 3 3
1 4 1
2 3 4
3 4 1
输出样例#1:
4
输入样例#2:
4 5
1 2 1
1 3 3
1 4 1
2 3 4
3 4 2
输出样例#2:
5
说明
【样例解释1】
小明选定让赞助商打通了 1 号宝藏屋。小明开发了道路 1→2,挖掘了 2 号宝藏。开发了道路 1→4,挖掘了 4 号宝藏。还开发了道路 4→3,挖掘了 3 号宝 藏。工程总代价为:1×1+1×1+1×2=4
【样例解释2】
小明选定让赞助商打通了 1 号宝藏屋。小明开发了道路 1→2,挖掘了 2 号宝藏。开发了道路 1→3,挖掘了 3 号宝藏。还开发了道路 1→4,挖掘了 4 号宝 藏。工程总代价为:1×1+3×1+1×1=5
【数据规模与约定】
对于 20%的数据: 保证输入是一棵树,1≤n≤8,v≤5000 且所有的 v 都相等。
对于 40%的数据: 1≤n≤8,0≤m≤1000,v≤5000 且所有的 v 都相等。
对于 70%的数据: 1≤n≤8,0≤m≤1000,v≤5000。
对于 100%的数据: 1≤n≤12,0≤m≤1000,v≤500000。
考场上我居然轻易地按照最短路的思想做了这题,对着数据来回搞,最后只搞了40分-_- 居然忘了状压这一回事……
下面是鄙人的题解
聪明的人说:第二天的dp来了(n<=12,不来一发状压dp还想干啥?)。
愚蠢的人说:第二天的暴力来了(n<=12,不来一发暴力还想干啥?)。
通过上面两句,相信大家已经知道,这题肯定跟dp有关系了。
然而你知道这题为什么会放到d2t2吗?
(消息来自知乎):据出题人还是谁透露,这题本来是放在d2t3的,而列队那题原来放在d2t2,结果验题人一发暴力A了这题(出题人本来是想考察状压dp的),于是两题就被调换位置了。
于是今年的Day2难得可以不写dp了!但这题我想说一下部分分的做法,因为部分分给的不错。20-pts:原图是树,从起点到每个宝藏屋只有唯一道路,按照唯一的道路挖就行了。
40-pts:所有道路长度相等,此时挖路的代价只与经过的宝藏屋数量 K 有关,因此求从起点到其它宝藏屋的单源最短路,按照最短路挖就是最优解。
70-pts:到这里肯定不能写最短路了,因为道路长度不同,离起点远的边的开发代价参数 K 又大,按最短路开发的代价不一定是最优解(比如从起点到某一个宝藏屋可以连着打2条长度为10的路(在一条路径上,即到终点的距离为20) 或 打一个每条边长度分别为1-2-3-4-5的路,前者的代价明显更小,但后者的路径却更短)。因此直接暴力dfs。
100-pts:见下
○方法1:状压dp(暂缺代码,码好了就发)
○方法2:dfs
用 dp[i] 来表示状态 i 下的最优方案,dis[j] 表示 j 到根节点的距离(题目中所描述的 K),用 dfs 来更新答案。状压dp就变成了记忆化搜索。
#include<bits/stdc++.h>
#define inf 2147483647
using namespace std;
int dp[1<<13],dis[15],G[15][15],isG[15][15],n,m,ans=inf;
//isG表示x,y之间是否有边
//点只有十二个直接上邻接矩阵即可
void insert(int x,int y,int w){G[x][y]=w;G[y][x]=w;isG[x][y]=1;isG[y][x]=1;}
//插边函数
void dfs(int x){
for(int i=1;i<=n;i++){
//枚举你所选点集中的每个点
if((1<<(i-1)) & x){
for(int j=1;j<=n;j++){
if(!(1<<(j-1)&x) && isG[i][j]) //判断能否选
if(dp[1<<(j-1)|x]>dp[x]+dis[i]*G[i][j]){ //有没有更新的必要
int temp=dis[j];
dis[j]=dis[i]+1;
dp[1<<(j-1)|x]=dp[x]+dis[i]*G[i][j];
dfs(1<<(j-1)|x);
dis[j]=temp;
}
}
}
}
}
int main(){
scanf("%d%d",&n,&m);
memset(G,63,sizeof(G)); //赋较大初值
for(int i=1;i<=m;i++){
int x,y,w;
scanf("%d%d%d",&x,&y,&w);
if(w<G[x][y])insert(x,y,w);
}
for(int i=1;i<=12;i++){
memset(dis,63,sizeof(dis));
for(int j=1;j<=(1<<n)-1;j++) dp[j]=inf;
//每枚举一遍根节点就重置一遍
dis[i]=1; dp[1<<(i-1)]=0;
dfs(1<<(i-1));
ans=min(ans,dp[(1<<n)-1]); //看答案是否能更新
}
printf("%d",ans);
return 0;
}
○方法3:bfs(来自wxj神爷的考场代码,不得不膜拜啊,这年代还手撸队列)
跟dfs差别不大,把挖到的宝藏屋的信息 塞到队列里而已,
#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
#define LL long long
using namespace std;
inline LL read(){
LL x=0,f=1;char c=getchar();
for(;!isdigit(c);c=getchar()) if(c=='-') f=-1;
for(;isdigit(c);c=getchar()) x=x*10+c-'0';
return x*f;
}
const int INF = 9999999;
const int MAXN = 100001;
LL N,M;
struct data{ //记录宝藏屋信息
LL ans;
LL dist[12+1]; //dist[i]表示从起点到i号点经过的宝藏屋数量,即题目中的K
LL ct; //ct表示宝藏屋编号
}Que[(1<<17)+1];
LL Root[MAXN+1],Node[MAXN+1],Cost[MAXN+1],Next[MAXN+1];
LL cnt, vis[(1<<17)]; //vis数组记录到每个宝藏屋的最低费用
void insert(int u,int v,int w){ //邻接表 不过跟我的风格差的有点多
++cnt; Node[cnt]=v; Cost[cnt]=w; Next[cnt]=Root[u]; Root[u]=cnt;
return;
}
LL ans=INF;
LL BFS(int f){
int head=1,tail=1;
for(int i=1;i<=N;i++) Que[tail].dist[i]=INF;
Que[tail].dist[f]=1; Que[tail].ans=0; //从起点到起点经过1个宝藏屋,且免费开通,无代价
for(int i=1;i<(1<<N);i++) vis[i]=INF;
Que[tail].ct=(1<<(f-1)); vis[(1<<(f-1))]=0; //刚开始的状态为只到过起点f
while(head<=tail)
{
data p=Que[head++];
if(vis[p.ct]<p.ans) continue; //当前解不比最优解更优,直接退
for(int k=1;k<=N;k++)
{
if( !(p.ct & (1<<(k-1))) ) continue; //判断当前宝藏屋p.ct是否已到过,如果(在状态中)没到过就退。也就是说只能从到过的宝藏屋出发
for(int x=Root[k];x;x=Next[x]) //用邻接表找宝藏屋出边
{
int v=Node[x];
if(p.ct & (1<<(v-1))) continue; //判断当前宝藏屋p.ct是否已到过,如果(在状态中)到过就退
data t=p;
t.ans+=(t.dist[k]*Cost[x]); //记录答案
t.ct=t.ct|(1<<(v-1));
if(vis[t.ct]<=t.ans) continue;
vis[t.ct]=t.ans; t.dist[v]=t.dist[k]+1;
Que[++tail]=t;
}
}
}
return vis[(1<<N)-1];
}
int main(){
N=read(),M=read();
for(int i=1;i<=M;i++){
LL u=read(),v=read(),w=read();
insert(u,v,w); insert(v,u,w);
}
for(int i=1;i<=N;i++)
ans=min(ans,BFS(i)); //直接枚举起点然后bfs
printf("%lld\n",ans);
}
我的得分:40
6.列队
题目描述
Sylvia 是一个热爱学习的女♂孩子。
前段时间,Sylvia 参加了学校的军训。众所周知,军训的时候需要站方阵。
Sylvia 所在的方阵中有n×m名学生,方阵的行数为 n,列数为 m。
为了便于管理,教官在训练开始时,按照从前到后,从左到右的顺序给方阵中 的学生从 1 到 n×m 编上了号码(参见后面的样例)。即:初始时,第 i 行第 j 列 的学生的编号是 (i−1)×m+j。
然而在练习方阵的时候,经常会有学生因为各种各样的事情需要离队。在一天 中,一共发生了 q件这样的离队事件。每一次离队事件可以用数对(x,y)(1≤x≤n,1≤y≤m)描述,表示第 x 行第 y 列的学生离队。
在有学生离队后,队伍中出现了一个空位。为了队伍的整齐,教官会依次下达 这样的两条指令:
1. 向左看齐。这时第一列保持不动,所有学生向左填补空缺。不难发现在这条 指令之后,空位在第 x 行第 m 列。
2. 向前看齐。这时第一行保持不动,所有学生向前填补空缺。不难发现在这条 指令之后,空位在第 n 行第 m 列。
教官规定不能有两个或更多学生同时离队。即在前一个离队的学生归队之后, 下一个学生才能离队。因此在每一个离队的学生要归队时,队伍中有且仅有第 n 行 第 m 列一个空位,这时这个学生会自然地填补到这个位置。
因为站方阵真的很无聊,所以 Sylvia 想要计算每一次离队事件中,离队的同学 的编号是多少。
注意:每一个同学的编号不会随着离队事件的发生而改变,在发生离队事件后 方阵中同学的编号可能是乱序的。
输入输出格式
输入格式:
输入共 q+1 行。
第 1 行包含 3 个用空格分隔的正整数 n,m,q,表示方阵大小是 n 行 m 列,一共发生了 q 次事件。
接下来 q 行按照事件发生顺序描述了 q 件事件。每一行是两个整数 x,y,用一个空 格分隔,表示这个离队事件中离队的学生当时排在第 x 行第 y 列。
输出格式:
按照事件输入的顺序,每一个事件输出一行一个整数,表示这个离队事件中离队学生的编号。
输入输出样例
输入样例#1:
2 2 3
1 1
2 2
1 2
输出样例#1:
1
1
4
说明
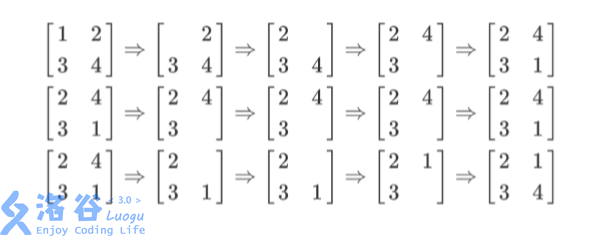
【输入输出样例 1 说明】
列队的过程如上图所示,每一行描述了一个事件。 在第一个事件中,编号为 1 的同学离队,这时空位在第一行第一列。接着所有同学 向左标齐,这时编号为 2 的同学向左移动一步,空位移动到第一行第二列。然后所有同 学向上标齐,这时编号为 4 的同学向上一步,这时空位移动到第二行第二列。最后编号 为 1 的同学返回填补到空位中。
【数据规模与约定】
数据保证每一个事件满足 1≤x≤n,1≤y≤m。
没错,这次的boss来了——但为什么是树巨结垢题啊……
考场上我大概留了1h准备手爆这题。但我的基础太菜,很不幸所有部分分都打炸了,不过由于官方数据太水,打错的前30分暴力 居然还搞到了25分……
所以不要再问我考试时爆炸的心态了……这种题一般就要拼部分分,那就开讲部分分吧。
30-pts
直接取出出队点放到右下角,然后平移询问所在的行 和 最后一列。 这是考场必打的辣鸡暴力。
50-pts
也就是说有效的行数(即参与询问的行数)不超过500行。我们把这些行离散化,那么就只需要维护一个q*m大小的方阵了(500*50000=2500W),直接开数组+暴力随便跑。
但由于最后一列的平移操作是不能离散化的,因此单开一个数组给最后一列取出询问所在行的点,暴力将后面部分前移,然后把该点放到最后。最后一列的操作 的单次复杂度O(n),总共做q次,该操作的总复杂度为O(nq),也随便跑。
只能离散化行,列是无法离散化的,多想想就明白了。
70-pts(n=x=1的20分)
80-pts(n≠1,x=1的10分)
所有询问都只对第一行进行操作,看起来跟n=1的20分做法没什么区别。手玩一下就会发现此时只有第一行和最后一列的数会发生变化,再仔细一点就会发现其实只是在第一行后面接上最后一列,然后就跟n=1的20分做法完全无区别了。于是把第一行和最后一列都放入树状数组里,像70-pts一样搞。
当然,有人可能并不想把第一行和最后一列接在一起(第一行最后一个数算在最后一列中,这样第一行就只存前m-1个数。这样的存法在100分做法中有实际作用!),那就给第一行和最后一列各单独做一个树状数组和arr数组,每次出队时都在第一行中删去这个点,接到最后一列的尾部,然后把最后一列的第一个数删去,接到第一行的尾部。实际上,这个做法引申了100分做法——因为对于每行你都可以类似这种操作,与最后一列实现快速“平移”呀!
****经过一系列的操作之后,其实上面的操作就剩下一个难点:怎么在O(log n)的时间内做到二分查询前缀和为k的最左位置?如果你想到了,再结合上一段说的内容,那恭喜你,你可以做100分做法了。
100-pts
70/80-pts已经大力提醒你了~
友情提示:在看下面的方法之前,你要做好仔细研读代码的准备,因为代码挺复杂的,不好理解,需要你缕清每一步在干什么。
○方法1:树状数组(官方标解,个人理解了1天;速度最快,最慢的点跑488ms)
正解概述:给每一行前m-1个数和最后一列各开一个树状数组和arr数组,利用树状数组在log级别的时间内查找出队点,然后快速将其移到最后一列尾部,再将最后一列于本行的数接到本行尾部。
但现在还剩下一个棘手的数据结构问题——直接开30w*30w的二维数组会爆!那我们能只用一维数组把他们都存下来吗?能!下面我从头分析整个想法过程:
我们观察到对于本来就在这一行中的元素,我们可以直接算出它的值,而不用存储。
怎么算呢?
定义一行中原来的元素为 初始时这一行前 m-1 个元素中,没有离队过的元素。
将所有出队点以 横坐标为第一关键字、输入编号为第二关键字 从小到大排序(就是优先以横坐标从小到大排序)。我们发现这时有一些出队点一定是原来的元素,那我们就可以用树状数组预处理出这些原来的元素的答案了。
预处理:考虑到x=1的30分的做法中,只有一行(n≠1,x=1时加一列)的数进行出队、加入队尾操作。在这里,每一个出队点都只会对本行 和 最后一列的点造成平移,当两个出队点不在最后一列 且 不在同一行的时候,它们不会不相互影响,因此我们依然可以对每一行用 m-1 位的树状数组,维护一个同70/80-pts中的01序列。但由于现在出队的点是加入了整个队列的右下角,而不是本行的最右侧,因此我们代入了原来的元素这个定义。这样在一行中的一个点出队时,我们只把那一位设成0,而不把这个数放到队尾,即不在队尾添加一个1。此时,由于本行的第m个数平移到了第m-1位,而第m列,也就是最后一列的数由于在每一次操作后都会向上平移一次而不是任何一行原来的元素,这一行的最后就会多出一个非原来的元素,因此我们记录一下本行m-1个数中最后有几个连续的非原来的元素,如果出队点不是原来的元素(即在最后非原来的元素那块)就不预处理。
当两个出队点在同一行的时候,它们之间会相互影响,必须按照输入顺序出队,因此输入编号作为第二关键字排序。
其实,不必对每一行都开一个树状数组,只需要开一个一行的树状数组,预处理下一行的时候把树状数组初始化就好了。
预处理操作后,要把树状数组清空,下面的操作对树状数组的用法与之前不同!
这下我们就预处理完了一部分询问的答案。对于剩下的不是原来的元素,我们发现,由于最多只有q(30w)个点出队,并且这些不是原来的元素一定是从最后一列平移过来的(重点!),我们很容易想到每行有几个点出队,最后一列就有几个点入这行的队尾(记住这个关键词!)。
因此我们可以把一个30w位的数组分割出n块,每行对应一块,且每行对应的块的大小为 该行要出队的点的数量。记录相邻两行之间的分割点,把每块都搞成一棵树状数组,这样每行就对应了一棵树状数组。每行对应的树状数组只存储最后一列平移到本行的点,这样本行有几个点出队,最后一列就有几个点入这行,这就是为什么每行对应的树状数组的大小为 该行要出队的点的数量。由于这些非原来的元素是从最后一列平移过来的,因此我们还得单开一个树状数组,用于存储最后一列。注意在开树状数组的时候要同步开arr数组。(其实可以用30w+1个vector来代替这个方法,每行对应一个vector,最后一列再单开一个,就不用考虑每行树状数组要开多大了。但由于时间关系,我就不码这个版本的代码了,下面的代码用的还是把数组分割成n块的方式)
做好了每行的树状数组,还得考虑一下它该怎么用。
我们可以记录一下每个出队点在本行的位置 的前面 有几个原来的元素,这样这个点的 列数(在本行的位置) - 前面原来的元素的数量,就得到了这个点是本行第几个非原来的元素(不要忘了没有预处理过的点都是非原来的元素)。这样就可以按类似70-pts中叙述的 二分找到第k个数 的思想,使用80-pts方法的最后一段提到的那个要求你想到的方法——在O(log n)时间内二分查询前缀和为k的最左位置,在本行的树状数组中用log级别的时间找到这个点,然后对它进行一系列操作。
那怎么操作呢?我们按照输入顺序对每个出队点进行操作:
如果这个出队点已经预处理过答案,就从本行的队列中直接取出它,接到最后一列的尾部;然后利用最后一列的树状数组,二分找到最后一列在本行的点,将其所在位置删除,并把这个点接到本行的尾部。
如果这个出队点没有预处理过答案,说明它不是原来的元素。先记录这个点的答案,然后分两种情况:
1.这个点不在最后一列,说明这个点的数是从最后一列平移过来的。利用本行的树状数组,二分找到这个点,将其所在位置删除,并把这个点接到最后一列的尾部。然后利用最后一列的树状数组,二分找到最后一列在本行的点,将其所在位置删除,并把这个点接到本行的尾部;
2.这个点在最后一列,那直接利用最后一列的树状数组,二分找到最后一列在本行的点,将其所在位置删除,并把这个点接到最后一列的尾部。
注意:树状数组和arr数组要一直同步更新,因为通过树状数组二分找到的第k个数 要在arr数组中的对应位置找到值!
树状数组版正解的复杂度:
时间复杂度 O(q log 玄学)【“玄学”大约为n+m+q这个级别?】
空间复杂度 O(n+2q)【所有行的树状数组大小加起来为q,最后一列的树状数组大小为n+q,因此最大的数组(即树状数组和arr数组)都是n+2q位】


1 #include<bits/stdc++.h> 2 using namespace std; 3 inline int read(){ 4 int x=0;bool f=1;char c=getchar(); 5 for(;!isdigit(c);c=getchar()) if(c=='-') f=0; 6 for(;isdigit(c);c=getchar()) x=(x<<3)+(x<<1)+c-'0'; 7 if(!f) return 0-x; 8 return x; 9 } 10 int n,m,q,tot; 11 int x[501]; 12 long long a[501][50001]; 13 vector<long long> que; 14 map<int,int> lsh,rlsh; 15 struct query{ 16 int x,y; 17 }qr[501]; 18 19 int main() 20 { 21 n=read(),m=read(),q=read(); 22 int i,j; 23 for(i=1;i<=q;i++) x[i]=qr[i].x=read(),qr[i].y=read(); 24 sort(x+1,x+q+1); 25 lsh[++tot]=x[1], rlsh[x[1]]=tot; 26 for(i=2;i<=q;i++){ 27 if(x[i]!=x[i-1]) lsh[++tot]=x[i]; 28 rlsh[x[i]]=tot; 29 } 30 31 for(i=1;i<=tot;i++) 32 for(j=1;j<=m;j++) 33 a[i][j]=(long long)(lsh[i]-1)*m+j; 34 35 que.push_back(0); 36 for(i=1;i<=n;i++) que.push_back((long long)i*m); 37 int tmp,xx,yy; 38 for(i=1;i<=q;i++){ 39 xx=rlsh[qr[i].x], yy=qr[i].y; 40 printf("%lld\n",a[xx][yy]); 41 tmp=a[xx][yy]; 42 43 for(j=yy+1;j<=m;j++) a[xx][j-1]=a[xx][j]; 44 que.erase(que.begin()+qr[i].x); 45 que.push_back(tmp); 46 47 for(j=xx;j<=tot;j++) a[j][m]=que[lsh[j]]; 48 } 49 return 0; 50 }


1 #include<cstdio> 2 #include<cctype> 3 #include<cstring> 4 #include<algorithm> 5 using namespace std; 6 #define ll long long 7 inline ll read(){ 8 ll x=0;bool f=1;char c=getchar(); 9 for(;!isdigit(c);c=getchar()) if(c=='-') f=0; 10 for(;isdigit(c);c=getchar()) x=(x<<3)+(x<<1)+c-'0'; 11 if(!f) return 0-x; 12 return x; 13 } 14 15 int q,id[300010]; 16 long long n,m,a[300010],b[300010]; 17 18 int h[300010],len[300010],len2[300010],bit[900010]; //bit(树状数组)最多用n+q位 19 long long arr[900010],ans[300010]; 20 21 inline bool cmp(int p1,int p2){return a[p1]==a[p2] ? p1<p2 : a[p1]<a[p2];} //按照行从小到大排序 22 23 inline int lowbit(int x){return x&-x;} 24 inline void add(int *array,int siz,int i,int x){ 25 for(;i<=siz;i+=lowbit(i)) array[i]+=x; 26 } 27 inline int query(int *array,int siz,int x){ //查找树状数组中第一个前缀和为x的位置 28 int l=1,r,mid,sum,ans; 29 while(l<=siz && array[l]<x) l<<=1, ans=l; //由于树状数组的第1位、第2位。第4位、第8位等2的倍数位 都直接存前缀和,因此通过它们找到x在哪两个前缀和区间,在这个区间里二分即可。挖槽,学到了,还能这么操作 30 r=l; sum=array[l>>=1]; //sum预设成树状数组在区间左端位置的前缀和 31 while(l<r-1){ 32 mid=l+r>>1; 33 if(mid>siz || array[mid]+sum>=x) r=mid, ans=mid; //array[mid]+sum=x 说明mid位进了答案x区间 34 else l=mid, sum+=array[l]; 35 /*上一行 36 1.这个树状数组前缀和求得太神了!利用二分代替 反向代替lowbit!orz 37 2.此时mid明显不是答案,但由于l设成了mid(正常是mid+1),二分结束时l和r差1,此时r是答案x的最左边一位,l是答案x区间的左边一位 38 */ 39 } 40 ans=r; 41 return ans; 42 } 43 44 int stk[300001],top; 45 int main(){ 46 int i; 47 n=read(),m=read(),q=read(); 48 for(i=1;i<=q;i++) a[i]=read(),b[i]=read(),id[i]=i; //a行 b列 49 sort(id+1,id+q+1,cmp); //将id按照行(a)从小到大排序 50 for(i=1;i<=m-1;i++) add(bit,m-1,i,1); //初始化每一位都是原来元素(即未被删除) 51 for(i=1;i<=n;i++) len[i]=m-1; //此时的len[i]记录第i行有几个 原来的元素 52 53 //预处理部分,方法跟80-pts部分基本相同 54 for(i=1;i<=q;i++){ 55 if(a[id[i-1]]!=a[id[i]]) //(a升序排列时)如果相邻两个a不相同 56 while(top) add(bit,m-1,stk[top--],1); //将树状数组初始化(前m-1个点都为1,后面的都为0)。我们只要把上一行做过-1操作的位置都记录下来,这里再把1加回去即可。 57 if(b[id[i]]>len[a[id[i]]]) continue; //b[id[i]]表示第i个询问的列,len[a[id[i]]]表示第i个询问所在行剩余的 原来的元素。意思:如果这个询问的位置不是原来元素就不预处理 58 //这个位置是原来元素,直接预处理答案 59 int pos=query(bit,m-1,b[id[i]]); //查询这个点到底在本行第几个 60 ans[id[i]] = (a[id[i]]-1)*m + pos; //直接根据横纵坐标计算出这个点的值 61 add(bit,m-1,pos,-1); //更新这个点为0,即被删除 62 stk[++top]=pos; 63 --len[a[id[i]]]; 64 } 65 //求剩下的 非原来的元素 的答案 66 //tip:数组+q 代表一个指针,指向数组的第q位,即在函数中以第q位为第1位 进行一系列操作 67 //bit + h[i]开的是第i行的树状数组,用来存储 最后一列滚来的数(非原来的元素),初始情况下都是0 68 //bit + h[n+1]开的是最后一列的树状数组,初始情况下1~n位都是1 69 70 //初始化h数组,h数组用于记录每行的树状数组的起始位置 71 int iter=0; 72 for(i=1;i<=n;i++){ 73 while(iter<=q && a[id[iter]]<i) ++iter; 74 h[i]=iter-1; //寻找最大的iter,使第iter个横坐标小于i。意思是寻找前一行最右边的一个离队点,那么 iter+x 就指向了第i行的树状数组的第x个数 75 } 76 h[n+1]=q; //最后一列的树状数组在第q位之后存,前面q位留给每行开树状数组 77 78 memset(bit,0,sizeof bit); //清空树状数组,重新使用它。之后的树状数组存每一行的非原来元素 79 for(i=1;i<=n;i++) len[i]=0, len2[i]=m-1; //此时的len[i]记录第i行最后接了几个最后一列滚来的数(非原来的元素);len2[i]记录第i行有几个原来的元素 80 len[n+1]=n; 81 82 for(i=1;i<=n;i++) add(bit+h[n+1],n+q,i,1), arr[q+i]=i*m; //arr[q+i]位记录最后一列第i行的数 83 for(i=1;i<=q;i++){ 84 if(ans[i]){ //这个点预处理过答案了 85 int pos=query(bit+h[n+1], n+q, a[i]); //在最后一列的树状数组查询本行(ai)的数所在的位置 86 87 add(bit+h[n+1], n+q, pos, -1); //更新这个点为0,即被删除 88 add(bit+h[n+1], n+q, ++len[n+1], 1); //把这个点接到最后一列尾部,在树状数组尾部加一个1(它出队留下的空就不补了) 89 arr[h[n+1] + len[n+1]] = ans[i]; //把这个出队点放入最后一列的最后一位 90 91 add(bit+h[a[i]],h[a[i]+1]-h[a[i]],++len[a[i]],1); //将最后一列在本行的点 向左平移一位 至本行的第m-1位,所以要在本行的树状数组最后接一个1,代表接了一个数 92 arr[h[a[i]]+len[a[i]]] = arr[h[n+1]+pos]; //把数值也搬到本行最后的对应位 93 --len2[a[i]]; //本行多了一个 非原来的元素 94 } 95 else{ //没预处理过答案,说明不是原来的元素 96 int pos = query(bit+h[n+1],n+q,a[i]); //在单独的树状数组查询第ai大的数 97 98 add(bit+h[n+1],n+q,pos,-1); //更新这个点为0,即被删除 99 add(bit+h[n+1],n+q,++len[n+1],1); //把这个点接到队尾,在树状数组尾部加一个1(它出队留下的空就不补了) 100 101 if(b[i] != m){ //如果这个点不在最后一列 102 int pos2 = query(bit+h[a[i]], h[a[i]+1]-h[a[i]], b[i]-len2[a[i]]); //b[i]-len2[a[i]]=列数-本行有几个原来的元素=这个点是本行第几个 非原来的元素。意思:求自己在本行树状数组中的第几位 103 add(bit+h[a[i]], h[a[i]+1] - h[a[i]], pos2, -1); //取出这个点,即在树状数组中将其设为0 104 ans[i] = arr[h[a[i]] + pos2]; //把这个数的值代入答案 105 add(bit+h[a[i]], h[a[i]+1] - h[a[i]], ++len[a[i]], 1); //将最后一列在本行的点 向左平移一位 至本行的第m-1位,所以要在本行的树状数组最后接一个1,代表接了一个数 106 arr[h[a[i]]+len[a[i]]] = arr[h[n+1]+pos]; //把数值也搬到本行最后的对应位 107 } 108 else ans[i] = arr[h[n+1] + pos]; //直接取出最后一列在本行的点,这个点就是出队点 109 arr[h[n+1] + len[n+1]] = ans[i]; //把这个点接到队尾 110 } 111 } 112 for(i=1;i<=q;i++) printf("%lld\n",ans[i]); //每一个询问的答案离线查询出答案了 113 return 0; 114 }
该做法最初借鉴于本大佬,感谢他的题解:https://www.luogu.org/space/show?uid=10703。:-)
○方法2:线段树(CCF老爷机严重卡常,因此动态开点)
暂时没写
○方法3:平衡树(splay)(非noip考查内容,理解难度低一点;速度最慢,最慢的点跑1800ms)
2018.10.7 update(好吧,我承认,现在弄题解没以前那么认真,简洁了一些):
我们观察每一行除了最后一个数之外的数在操作中是如何变化的。
如果出队在 $(x,y)$,那么第$x$行(除了最后一个数)会弹出第$y$个数,它后面的数依次左移,再在最后插入一个数(就是最后一列当前的第$x$个数);然后,对于最后一列,我们要弹出第$x$个数(插入到第$x$行),再在最后插入一个数(就是刚出队的那个)。
所以,我们无论是对于行还是列,都要执行两种操作:第一,弹出第k个数,第二,在尾部插入一个数。可以用splay来实现。
但是这最多做到了二分优化时间,挨个存点的空间复杂度是$O(nm)$。
那怎么办?
跟用树状数组写的发现一样,我们发现$q$最大只有$300000$,有些人从始至终都是左右相邻的。
但splay是开的是点,而不是区间,所以跟树状数组不一样,不预处理那些始终不动的数。
利用splay的点存优势,我们在维护splay的时候,一段连续的数可以用一个节点维护,记录这个节点表示的区间的左右端点。
如果我们发现要弹出的数在某个节点内部,我们就把它拆成$3$个节点(其中中间那个节点只有一个数,就是我们要的那个数。其余两个节点分别存左半边和右半边),拆点操作这么做:把原节点表示区间的右端点左移,而右边减少的部分可以划为新增节点的表示区间。
时间复杂度还是 O(q log 玄学)【这个“玄学”就带很大的常数了,看你splay的优化和卡常情况】
空间复杂度还是 O(2n+2q)【对于前m-1列,一开始总共n个点(每行1个),每次询问最多会分离出2个点(分离前的点还在用!);对于第m列,一开始总共1个点,最多被分为n个点】
另外, 这个程序写了垃圾桶优化内存。


1 #include<bits/stdc++.h> 2 #define ll long long 3 #define N 300010 4 using namespace std; 5 inline int read(){ 6 int x=0; bool f=1; char c=getchar(); 7 for(;!isdigit(c);c=getchar()) if(c=='-') f=0; 8 for(; isdigit(c);c=getchar()) x=(x<<3)+(x<<1)+(c^'0'); 9 if(f) return x; 10 return 0-x; 11 } 12 13 int fa[N<<3],son[N<<3][2],cnt; 14 ll l[N<<3],r[N<<3],siz[N<<3]; 15 int rub[N],rub_cnt; 16 struct Splay{ 17 int root; 18 inline int newNum(){ 19 if(!rub_cnt) return ++cnt; 20 return rub[--rub_cnt]; 21 } 22 inline int newNode(ll L,ll R){ 23 int x=newNum(); 24 fa[x]=son[x][0]=son[x][1]=0; 25 siz[x]=(r[x]=R)-(l[x]=L); 26 return x; 27 } 28 inline void init(ll L,ll R){ 29 root=newNode(L,R); 30 } 31 inline void upd(int x){siz[x]=siz[son[x][0]]+siz[son[x][1]]+r[x]-l[x];} 32 inline int dir(int x){return son[fa[x]][1]==x;} 33 void rotate(int x){ 34 int d=dir(x),f=fa[x]; 35 fa[x]=fa[f]; 36 if(f==root) root=x; 37 else son[fa[f]][dir(f)]=x; //更新点x的爷爷节点的儿子 38 if(son[f][d]=son[x][d^1]) fa[son[f][d]]=f; 39 fa[son[x][d^1]=f] = x; 40 upd(f), upd(x); 41 } 42 void splay(int x){ 43 for(;fa[x];rotate(x)) 44 if(fa[fa[x]]) rotate(dir(x)==dir(fa[x]) ? fa[x] : x); //判断单双旋 45 } 46 int splitNode(int x,ll k){ //把节点x分裂,分裂后x的区间里前k个数还在x节点上,第k个及后边的数对应新节点 47 k+=l[x]; 48 int y=newNode(k,r[x]); 49 r[x]=k; 50 if(son[x][1]==0) fa[son[x][1]=y] = x; 51 else{ 52 int t=son[x][1]; 53 while(son[t][0]) t=son[t][0]; 54 fa[son[t][0]=y]=t; 55 while(t!=x) upd(t),t=fa[t]; 56 } 57 splay(y); 58 return y; //返回新分出的节点(后面一段) 59 } 60 61 inline void del(int o){ //splay删除 62 splay(o); 63 fa[son[o][0]]=fa[son[o][1]]=0; 64 if(!son[o][0]) root=son[o][1]; 65 else{ 66 int t=son[o][0]; 67 while(son[t][1]) t=son[t][1]; 68 splay(t); 69 upd(root = fa[son[t][1] = son[o][1]] = t); //将原根的右儿子更新给新根的右儿子,原根就没了(之前忘了写后面的=t!) 70 } 71 rub[rub_cnt++]=o; 72 } 73 ll popKth(ll k){ 74 int o=root; 75 while(1){ 76 if(k<=siz[son[o][0]]) o=son[o][0]; 77 else{ 78 k-=siz[son[o][0]]; 79 if(k<=r[o]-l[o]){ 80 if(k!=r[o]-l[o]) splitNode(o,k); //出队点不在最右端 才需要分出右边节点 81 if(k!=1) o=splitNode(o,k-1); //出队点不在最左端 才需要分出左边节点 82 break; 83 } 84 else{ 85 k-=r[o]-l[o]; //减去当前节点的大小 86 o=son[o][1]; 87 } 88 } 89 } 90 del(o); //删除出队点 91 return l[o]; 92 } 93 void pushBack(ll k){ 94 int y=newNode(k,k+1); 95 if(!root) root=y; 96 else{ 97 int o=root; 98 while(son[o][1]) o=son[o][1]; 99 splay(o); 100 upd(fa[son[o][1]=y] = o); 101 } 102 } 103 }s[N]; 104 int n,m,q; 105 int main(){ 106 n=read(),m=read(),q=read(); 107 ll i; 108 for(i=1;i<=n;i++) s[i].init((i-1)*m+1,i*m); 109 s[0].init(m,m+1); 110 for(i=2;i<=n;i++) s[0].pushBack(i*m); 111 int x,y; 112 ll p; 113 while(q--){ 114 x=read(),y=read(); 115 s[x].pushBack(s[0].popKth(x)); 116 printf("%lld\n",p=s[x].popKth(y)); 117 s[0].pushBack(p); 118 } 119 return 0; 120 }
该做法最初借鉴于本大佬,感谢他的题解:https://www.luogu.org/space/show?uid=7868。:-)
另外我重申一下:这种splay写法在OJ上交,是卡着2s的时限过的(标题说了最大点1800ms),但是在noip考场上不推荐写这种比较骚的数据结构,他们的老爷机会卡常数,可能导致最后几个点评测TLE了。来了解一下wzj52501神爷两小时打完day2然后最后一题被卡30分常的自闭经历
我的得分:25(哇你肯定很奇怪这是怎么拿的分吧?!没办法我人菜分也菜)
提高组总得分:295(北京省一分数线280+5,那5分名义上是惩罚而实际上是人性沦丧,考280分的人招谁惹谁了)
到这里我只有一句话想说了:我好菜,我要加油。
后记
好的,我已经愉快地翻掉了noip2017的车,下面我就要驶向更加残酷的noip2018了~
别以为蒟蒻没有梦想,我也希望有一天我的解题报告能上NOI年鉴的ToT
看完全文的福利(重点!):
The log:
2018.3.1 本文基础更新完毕时间(即所有题都发了至少一种题解)
2018.9.28 优化部分标题字体颜色
2018.10.7 修复提高组几道题因复制后没清干净格式 而导致的文字数学格式混乱->Math Processing Error