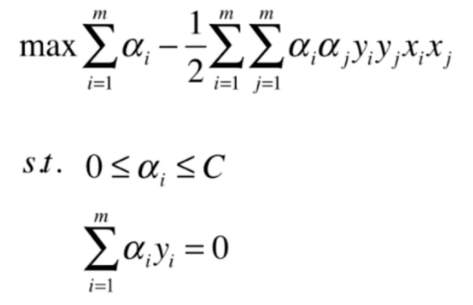Evernote Export
支持向量机(Support Vector Machine)
不适定问题不止一个决策边界
要找一个决策边界,不仅能将训练集很好的划分,而且提升模型的泛化能力
支持向量机直接将算法放在运行的内部,在不适定的问题中,使用svm去建模是好的
svm是统计学习中非常重要的方法
svm尝试寻找一个最优的决策边界,距离两个类别的最近的样本最远,距离决策边界最近的点称为支撑向量
svm算法要做的就是最大化margin,也就是要找到最大的d
margin=2d
解析几何,点到直线的距离
(x,y)到Ax+By+C=0的距离A2+B2∣Ax+By+C∣
扩展到n维空间θTxb=0-->wTx+b=0-->∣∣w∣∣wT+b
∣∣w∣∣=w12+w22+...+wn2
∣∣w∣∣wTxi+b≥d 其中∀yi=1
∣∣w∣∣wTxi+b≤−d 其中∀yi=−1
∣∣w∣∣dwTxi+b≥1 其中∀yi=1
∣∣w∣∣dwTxi+b≤−1 其中∀yi=−1
wdTxi+bd≥1其中∀yi=1
wdTxi+bd≤−1其中∀yi=−1
yi(wTxi+b)≥1
对于任意支撑向量x有 max∣∣w∣∣∣wTx+b∣-->max∣∣w∣∣1-->min21∣∣w∣∣2
Soft Margin和SVM的正则化
Soft Margin SVM yi(wTxi+b)≥1−ζ
ζi≥0
min21∣∣w∣∣2+C⋅Σi=1mζi
C为超参数,平衡两部分的重要程度
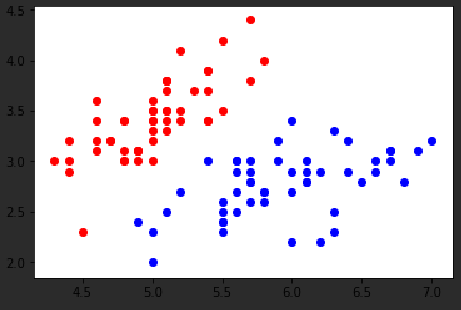
使用SVM需要对数据进行标准化处理
对于SVM上,数据尺度不同,需要对数据进行标准化处理
什么是核函数
svm的本质:其实就是求解最优化问题,求解最优化过程中,需要变形为数学中最好解决的问题
核函数思想:K(xi,xk)=xi,xj
K(x,y)=(x⋅y+1)2
K(x,y)=(i=1∑nx⋅y+1)2=i=1∑n(xi2)(yi2)+i=2∑nj=1∑i−1(2xixj)(2yiyj)+i=1∑n(2xi)(2yi)+1
核函数会降低原算法的复杂度
K(x,y)=(x⋅y+c)d
d就是函数里的degree
高斯核函数
K(x,y)表示x和y的点乘
K(x,y)=e−γ∣∣x−y∣∣2
正态分布就是高斯函数 g(x)=σ2π
1e−21(σx−μ)2
RBF核 Radial Basis Function Kernel
将每一个样本点映射到一个无穷维的特征空间
多项式特征依靠升维是的原本线性不可分的数据线性可分
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
iris = datasets.load_iris()
X = iris.data
y = iris.target
X = X[y < 2, :2]
y = y[y < 2]
plt.scatter(X[y == 0, 0], X[y == 0, 1], color='red')
plt.scatter(X[y == 1, 0], X[y == 1, 1], color='blue')
plt.show()
from sklearn.preprocessing import StandardScaler
standardScaler = StandardScaler()
standardScaler.fit(X)
X_standard = standardScaler.transform(X)
from sklearn.svm import LinearSVC
#SVC使用向量做分类
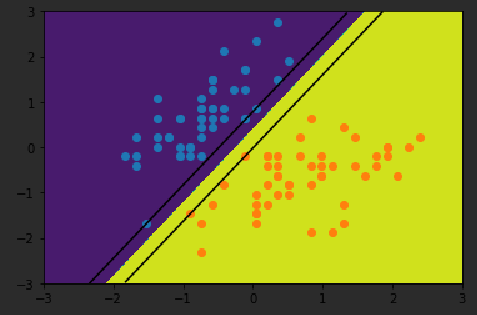
svc = LinearSVC(C=1e9)
svc.fit(X_standard, y)
def plot_decision_boundary(model, axis):
x0,x1 = np.meshgrid(
np.linspace(axis[0],axis[1],int((axis[1]-axis[0])*100)).reshape(-1,1),
np.linspace(axis[2],axis[3],int((axis[3]-axis[2])*100)).reshape(-1,1),
)
X_new = np.c_[x0.ravel(),x1.ravel()]
y_predict = model.predict(X_new)
zz = y_predict.reshape(x0.shape)
from matplotlib.colors import ListedColormap
custom_camp = ListedColormap(['#EF9A9A','#FFF59D','#90CAF9'])
plt.contourf(x0, x1, zz, linewith=5, camp=custom_camp)
w = model.coef_[0]
b = model.intercept_[0]
plot_x = np.linspace(axis[0], axis[1], 200)
up_y = -w[0]/w[1]*plot_x-b/w[1]+1/w[1]
down_y = -w[0]/w[1]*plot_x-b/w[1]-1/w[1]
up_index = (up_y>=axis[2])&(up_y<=axis[3])
down_index = (down_y>=axis[2])&(down_y<=axis[3])
plt.plot(plot_x[up_index],up_y[up_index],color='black')
plt.plot(plot_x[down_index],down_y[down_index],col
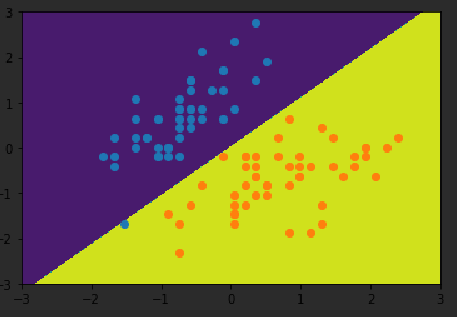
plot_decision_boundary(svc, axis=[-3,3,-3,3])
plt.scatter(X_standard[y==0,0],X_standard[y==0,1])
plt.scatter(X_standard[y==1,0],X_standard[y==1,1])
plt.show()
svc2 = LinearSVC(C=0.01)
svc2.fit(X_standard, y)
plot_decision_boundary(svc2, axis=[-3,3,-3,3])
plt.scatter(X_standard[y==0,0],X_standard[y==0,1])
plt.scatter(X_standard[y==1,0],X_standard[y==1,1])
plt.show()


#多项式处理非线性问题
import numpy as npimport matplotlib.pyplot as plt
from sklearn import datasets
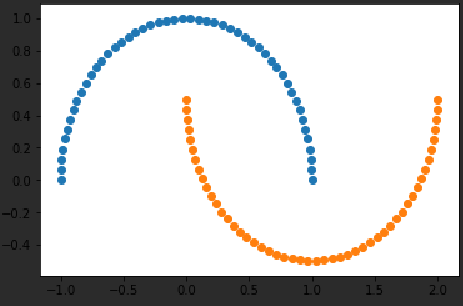
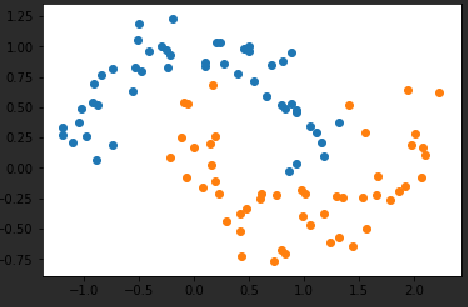
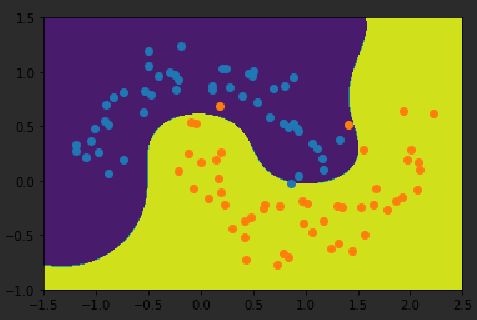
X, y = datasets.make_moons()
plt.scatter(X[y==0,0],X[y==0,1])plt.scatter(X[y==1,0],X[y==1,1])plt.show()
#构建数据集
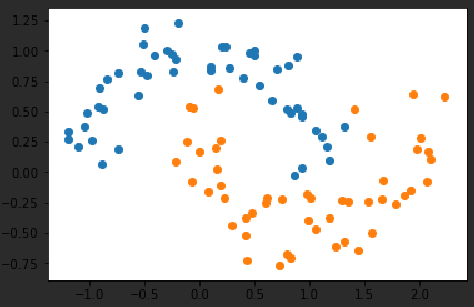
X,y = datasets.make_moons(noise=0.15, random_state=666)
plt.scatter(X[y==0,0],X[y==0,1])plt.scatter(X[y==1,0],X[y==1,1])plt.show()
from sklearn.preprocessing import PolynomialFeatures, StandardScaler
from sklearn.svm import LinearSVC
from sklearn.pipeline import Pipeline
def PolynomialSVC(degree,C=1.0):
return Pipeline([
("poly", PolynomialFeatures(degree=degree)),
("std_scaler", StandardScaler()),
("linearSVC", LinearSVC(C=C)),
])
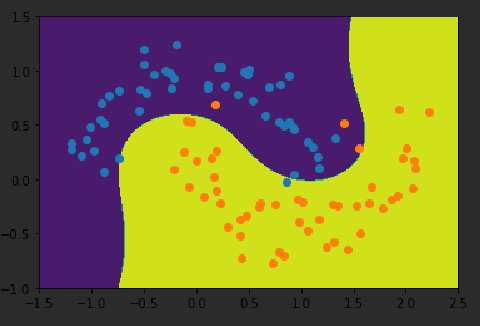
poly_svc = PolynomialSVC(degree=3)
poly_svc.fit(X,y)
def plot_decision_boundary(model, axis):
x0,x1 = np.meshgrid(
np.linspace(axis[0],axis[1],int((axis[1]-axis[0])*100)).reshape(-1,1),
np.linspace(axis[2],axis[3],int((axis[3]-axis[2])*100)).reshape(-1,1),
)
X_new = np.c_[x0.ravel(),x1.ravel()]
y_predict = model.predict(X_new)
zz = y_predict.reshape(x0.shape)
from matplotlib.colors import ListedColormap
custom_camp = ListedColormap(['#EF9A9A','#FFF59D','#90CAF9'])
plt.contourf(x0, x1, zz, linewith=5, camp=custom_camp)
plot_decision_boundary(poly_svc,axis=[-1.5,2.5,-1.0,1.5])
plt.scatter(X[y==0,0], X[y==0,1])
plt.scatter(X[y==1,0], X[y==1,1])
plt.show()
#多项式核函数
from sklearn.svm import SVC
def PolynomialKernelSVC(degree, C=1.0):
return Pipeline([
("std_scaler", StandardScaler()),
("kernelSVC", SVC(kernel='poly',degree=degree,C=C)),
])
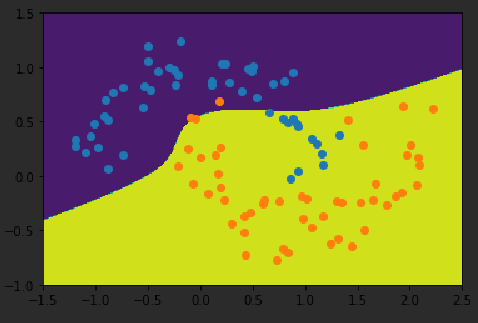
poly_kernel_svc = PolynomialKernelSVC(degree=3)
poly_kernel_svc.fit(X,y)
plot_decision_boundary(poly_kernel_svc,axis=[-1.5,2.5,-1.0,1.5])
plt.scatter(X[y==0,0], X[y==0,1])
plt.scatter(X[y==1,0], X[y==1,1])
plt.show()
scikit-learn的高斯核函数
K(x,y)=e^{-\gamma||x-y||}^2gamma越大,高斯分布越窄
gamma越小,高斯分布越宽
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
X, y = datasets.make_moons(noise=0.15, random_state=666)
plt.scatter(X[y == 0, 0], X[y == 0, 1])plt.scatter(X[y == 1, 0], X[y == 1, 1])
plt.show()
from sklearn.preprocessing import StandardScaler
from sklearn.svm import SVC
from sklearn.pipeline import Pipeline
def RBFkernelSVC(gamma=1.0):
return Pipeline([
("std_scaler", StandardScaler()),
("svc", SVC(kernel='rbf', gamma=gamma)),
])
svc = RBFkernelSVC(gamma=1.0)
svc.fit(X, y)
def plot_decision_boundary(model, axis):
x0,x1 = np.meshgrid(
np.linspace(axis[0],axis[1],int((axis[1]-axis[0])*100)).reshape(-1,1),
np.linspace(axis[2],axis[3],int((axis[3]-axis[2])*100)).reshape(-1,1),
)
X_new = np.c_[x0.ravel(),x1.ravel()]
y_predict = model.predict(X_new)
zz = y_predict.reshape(x0.shape)
from matplotlib.colors import ListedColormap
custom_camp = ListedColormap(['#EF9A9A','#FFF59D','#90CAF9'])
plt.contourf(x0, x1, zz, linewith=5,camp=custom_camp)
plot_decision_boundary(svc, axis=[-1.5, 2.5, -1.0, 1.5])
plt.scatter(X[y == 0, 0], X[y == 0, 1])
plt.scatter(X[y == 1, 0], X[y == 1, 1])
plt.show()
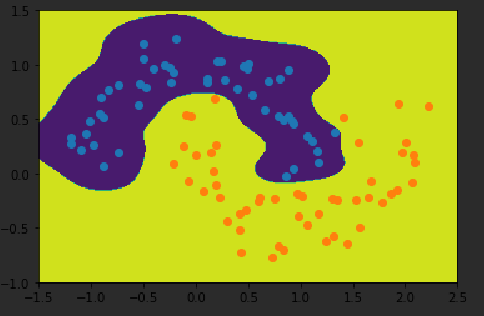
svc_gamma100 = RBFkernelSVC(gamma=100)
svc_gamma100.fit(X,y)
plot_decision_boundary(svc_gamma100, axis=[-1.5, 2.5, -1.0, 1.5])
plt.scatter(X[y == 0, 0], X[y == 0, 1])
plt.scatter(X[y == 1, 0], X[y == 1, 1])
plt.show()
#决策边界的这一类,其中在周围都形成了中型的图案
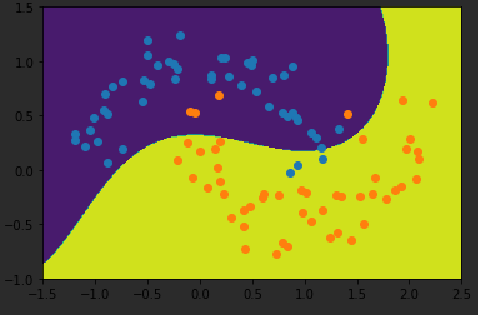
svc_gamma10 = RBFkernelSVC(gamma=10)
svc_gamma10.fit(X,y)
plot_decision_boundary(svc_gamma10, axis=[-1.5, 2.5, -1.0, 1.5])
plt.scatter(X[y == 0, 0], X[y == 0, 1])
plt.scatter(X[y == 1, 0], X[y == 1, 1])
plt.show()
svc_gamma03 = RBFkernelSVC(gamma=0.3)
svc_gamma03.fit(X,y)
plot_decision_boundary(svc_gamma03, axis=[-1.5, 2.5, -1.0, 1.5])
plt.scatter(X[y == 0, 0], X[y == 0, 1])
plt.scatter(X[y == 1, 0], X[y == 1, 1])
plt.show()
SVM思路解决回归问题
使用margin的方式,类似于soft margin svm方式
就是找两个距离余量,需要留着距离之间的距离
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
boston = datasets.load_boston()
X = boston.data
y = boston.target
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X,y,random_state=666)
from sklearn.svm import LinearSVR
from sklearn.svm import SVR
from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import Pipeline
def SrandardlinearSVR(epsilon=0.1):
return Pipeline([
("std_scaler", StandardScaler()),
("linearSVR", LinearSVR(epsilon=epsilon))
])
svr = SrandardlinearSVR()
svr.fit(X_train, y_train)
svr.score(X_test, y_test)