P1213 时钟

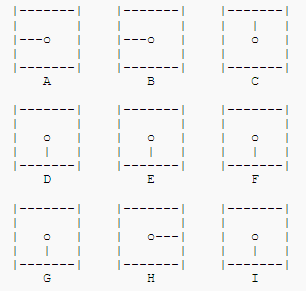
题目描述

考虑将如此安排在一个 3 x 3 行列中的九个时钟:

目标要找一个最小的移动顺序将所有的指针指向12点。下面原表格列出了9种不同的旋转指针的方法，每一种方法都叫一次移动。选择1到9号移动方法，将会使在表格中对应的时钟的指针顺时针旋转90度。

移动方法 受影响的时钟

1 ABDE

2 ABC

3 BCEF

4 ADG

5 BDEFH

6 CFI

7 DEGH

8 GHI

9 EFHI

Example

[但这可能不是正确的方法，请看下面]

输入格式

第1-3行: 三个空格分开的数字，每个数字表示一个时钟的初始时间，3,6,9,12。数字的含意和上面第一个例子一样。

输出格式

单独的一行包括一个用空格分开的将所有指针指向12:00的最短移动顺序的列表。

如果有多种方案，输出那种使其连接起来数字最小的方案。(举例来说5 2 4 6 < 9 3 1 1)。

输入输出样例

输入 #1复制

9 9 12
6 6 6
6 3 6 

输出 #1复制

4 5 8 9

说明/提示

题目翻译来自NOCOW。

USACO Training Section 1.4

 

我说它是暴力枚举，你信吗。。。。。。

 

#include <bits/stdc++.h>
using namespace std;
struct node{
    int state[9];
    string ans;
};
const bool movement[9][9] = 
{
  {1,1,0,1,1,0,0,0,0},
  {1,1,1,0,0,0,0,0,0},
  {0,1,1,0,1,1,0,0,0},
  {1,0,0,1,0,0,1,0,0},
  {0,1,0,1,1,1,0,1,0},
  {0,0,1,0,0,1,0,0,1},
  {0,0,0,1,1,0,1,1,0},
  {0,0,0,0,0,0,1,1,1},
  {0,0,0,0,1,1,0,1,1}
};
int state[9];
inline bool checkOK(int state[]){
    for(int i=0;i<9;i++){
        if(state[i] != 4) return false;
    }
    return true;
}
string ans = "";
bool vis[5][5][5][5][5][5][5][5][5];
queue<node> q;
void bfs(){
    node tt;
    for(int j=0;j<9;j++){
        tt.state[j] = state[j];
    }
    tt.ans = "";
    q.push(tt);
    while(!q.empty()){
        node now = q.front();
        q.pop();
        if(checkOK(now.state)){
            ans = now.ans;
            return;
        }
        for(int i=0;i<9;i++){
            node nextn=now;
            for(int k=0;k<9;k++){
                nextn.state[k]=(nextn.state[k]+movement[i][k])%5;
                if(nextn.state[k] == 0) nextn.state[k] = 1;
            }
            nextn.ans += (char)('0'+i+1);
            if(!vis[nextn.state[0]][nextn.state[1]][nextn.state[2]][nextn.state[3]][nextn.state[4]][nextn.state[5]][nextn.state[6]][nextn.state[7]][nextn.state[8]]){
                q.push(nextn);
                vis[nextn.state[0]][nextn.state[1]][nextn.state[2]][nextn.state[3]][nextn.state[4]][nextn.state[5]][nextn.state[6]][nextn.state[7]][nextn.state[8]] = true;
            }
        }
    }
}
int main(){
    ios::sync_with_stdio(false);
    cin.tie(0);
    for(int i=0;i<9;i++){
        int time;
        cin>>time;
        state[i] = time / 3;
    }
    memset(vis,false,sizeof vis);
    bfs();
    for(int i=0;i<ans.size();i++){
        if(i == 0){
            cout << ans[i];
        }else{
            cout << " " << ans[i];
        }
    }
    return 0;
}