本文目的是以一种通俗简单的方式介绍Ken Perlin的改进版柏林噪声算法,讲解代码采用c#编写,开源免费使用。如果你只是想看完整代码,点击这里。
柏林噪声是一个非常强大算法,经常用于程序生成随机内容,在游戏和其他像电影等多媒体领域广泛应用。算法发明者Ken Perlin也因此算法获得奥斯卡科技成果奖(靠算法拿奥斯卡也是没谁了666)。本文将剖析他于2002年发表的改进版柏林噪声算法。在游戏开发领域,柏林噪声可以用于生成波形,起伏不平的材质或者纹理。例如,它能用于程序生成地形(例如使用柏林噪声来生成我的世界(Minecraft)里的地形),火焰燃烧特效,水和云等等。柏林噪声绝大部分应用在2维,3维层面上,但某种意义上也能拓展到4维。柏林噪声在1维层面上可用于卷轴地形、模拟手绘线条等。
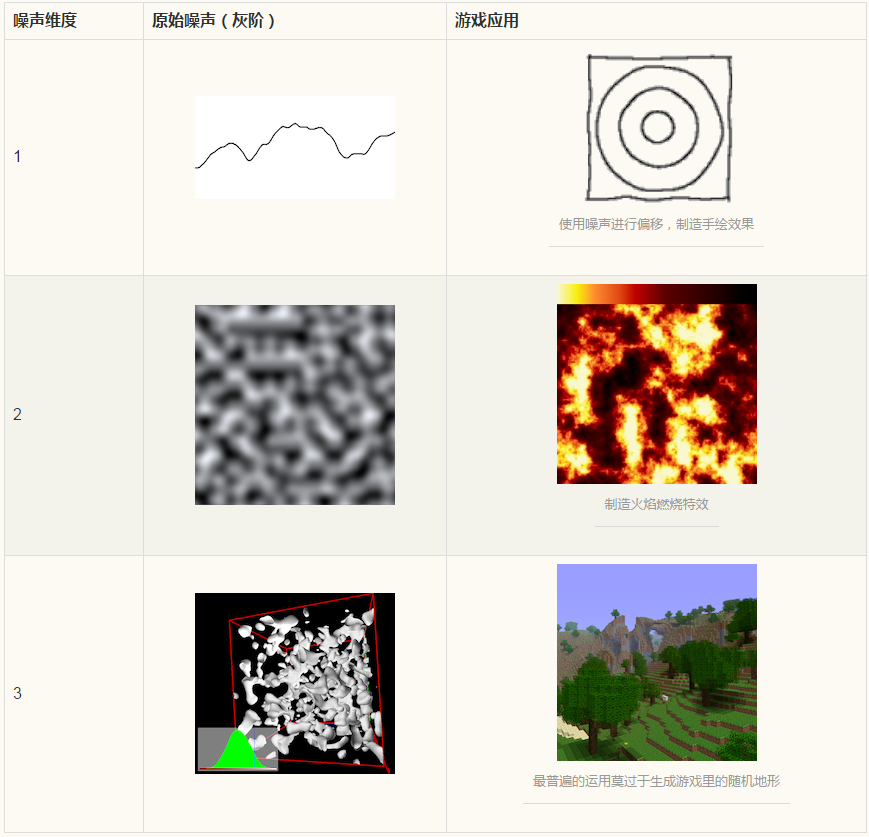
如果将柏林噪声拓展到4维层面,以第4维,即w轴代表时间,就能利用柏林噪声做动画。例如,2D柏林噪声可以通过插值生成地形,而3D柏林噪声则可以模拟海平面上起伏的波浪。下面是柏林噪声在不同维度的图像以及在游戏中的应用场景。
正如图所示,柏林噪声算法可以用来模拟许多自然中的噪声现象。接下来让我们从数理上分析算法的实现原理。
基本原理
注意:事先声明,本节内容大多源于this wonderful article by Matt Zucker,不过该篇文章内容也是建立在1980年所发明的柏林噪声算法基础上的。本文我将使用2002年发明的改进版柏林噪声算法。因此,我的算法版本跟Zucker的版本会有些不同。
让我们从最基本的柏林噪声函数看起:public double perlin(double x, double y, double z);
函数接收x,y,z三个坐标分量作为输入,并返回0.0~1.0的double值作为输出。那我们应该怎么处理输入值?首先,我们取3个输入值x,y,z的小数点部分,就可以表示为单元空间里的一个点了。为了方便讲解,我们将问题降维到2维空间来讨论(原理是一样的),下图是该点在2维空间上的表示:
图1:小蓝点代表输入值在单元正方形里的空间坐标,其他4个点则是单元正方形的各顶点
接着,我们给4个顶点(在3维空间则是8个顶点)各自生成一个伪随机的梯度向量。梯度向量代表该顶点相对单元正方形内某点的影响是正向还是反向的(向量指向方向为正向,相反方向为反向)。而伪随机是指,对于任意组相同的输入,必定得到相同的输出。因此,虽然每个顶点生成的梯度向量看似随机,实际上并不是。这也保证了在梯度向量在生成函数不变的情况下,每个坐标的梯度向量都是确定不变的。
举个例子来理解伪随机,比如我们从圆周率π(3.14159...)的小数部分中随机抽取某一位数字,结果看似随机,但如果抽取小数点后1位,结果必定为1;抽取小数点后2位,结果必定为4。
图2:各顶点上的梯度向量随机选取结果
请注意,上图所示的梯度向量并不是完全准确的。在本文所介绍的改进版柏林噪声中,这些梯度向量并不是完全随机的,而是由12条单位正方体(3维)的中心点到各条边中点的向量组成:(1,1,0),(-1,1,0),(1,-1,0),(-1,-1,0), (1,0,1),(-1,0,1),(1,0,-1),(-1,0,-1), (0,1,1),(0,-1,1),(0,1,-1),(0,-1,-1)
采用这些特殊梯度向量的原因在Ken Perlin's SIGGRAPH 2002 paper: Improving Noise这篇文章里有具体讲解。
注意:许多介绍柏林噪声算法的文章都是根据最初版柏林噪声算法来讲解的,预定义的梯度表不是本文所说的这12个向量。如图2所示的梯度向量就是最初版算法所随机出来的梯度向量,不过这两种算法的原理都是一样的。
接着,我们需要求出另外4个向量(在3维空间则是8个),它们分别从各顶点指向输入点(蓝色点)。下面有个2维空间下的例子:
图3:各个距离向量
接着,对每个顶点的梯度向量和距离向量做点积运算&#