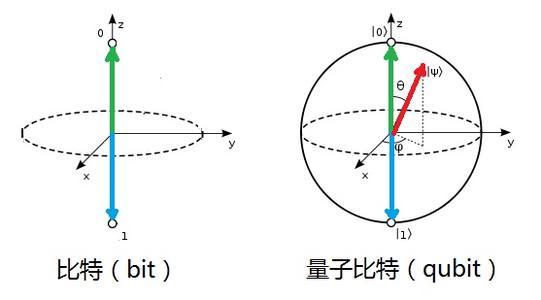
量子比特是量子计算和量子信息的基本概念,简写为qubit。
经典比特只能处在0或1态,就像是一枚硬币,不是正面朝上,就是反面朝上。而量子比特可以形成
![]()
和
![]()
的叠加态:
![]()
,其中
![]()
是复数。 换句话说,量子比特的态是二维复向量空间中的一个向量。
![]()
是计算基态,形成了这个向量空间的正交基。
但是,与经典情况不同,我们不能通过检测一个量子比特来确定它的量子态,即测量一个量子比特,我们不能得到
![]()
的值。根据量子力学,我们知道,测量一个量子比特,得到结果是0这个态的概率是
![]()
,而得到结果是1这个态的概率是
![]()
,显然
![]()
。这样,量子比特态就是二维复向量空间的一个单位向量。
也就是说,量子比特被检测之前一直处于介于
![]()
之间的一个连续态。而测量时,仅概率性的给出0或1作为测量结果。
例如,一个量子比特可以处于
![]()
态(常把这个态记为
![]()
态),测量的时候,百分之五十的概率得到0,百分之五十的概率得到1。
几何表示:因为
![]()
,量子比特的叠加态可以写为:
![]()
,这里的
![]()
是实数。因为
![]()
没有明显的效果,我们可以先忽略它。所以,可以简写为:
![]()
。
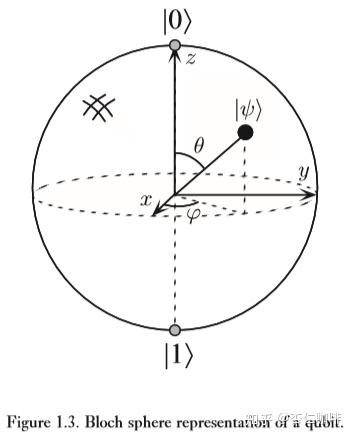
![]()
定义了单位三维球面上的一个点。这个球被称为Bloch球,如图
一些小补充:虽然在单位球面上有无数多个点,但是我们测量一个量子比特后,只可能得到0或1,而且,测量改变了这个量子比特的态,将它从
![]() 的叠加状态塌缩到与测量结果一致的态。例如,如果
的叠加状态塌缩到与测量结果一致的态。例如,如果
的测量结果是0,那么这个量子比特测量后的态就变为了
。这也是量子力学的基本假设之一。从单次测量中,我们只能得到关于单个量子比特的信息。只有无穷多个相同的量子比特被测量,才能够确定
,得到一个完整的叠加态方程
。当一个量子比特处于一个封闭的量子系统,并且不执行任何的“测量”时,显然这时候它记录了所有描述这个态的连续变量,如
。从某种意义上说,在量子比特态下,大自然隐藏了大量的“隐藏信息”。
1.2.1 多个量子比特
两个经典比特有四个可能的态:00,01,10和11。相应地,一个双量子比特的系统的计算基态是
![]()
。一对量子比特可以形成这四个态的叠加态,因此两个量子比特的量子态将一个复系数(有时称为振幅)与每个计算基态相关联,这样描述两个量子比特态的向量就是:
![]()
。
测量结果
![]()
发生的概率为
![]()
,测量后的量子比特的态是
![]()
。归一化条件:
![]()
,即
![]()
。
对于两个量子比特系统,我们可以测量量子比特的一个子集。比如,测量第一个量子比特为0的概率是
![]()
,测量后的态为:
![]()
。测量后的态由
![]()
重新归一化。
补充:一个重要的两个量子比特态是
Bell态(或EPR对):
。
Bell态的特性是,在测量第一个量子比特时,可以得到两个可能的结果:得到0概率为1/2,测量后的态为
![]()
;
得到1概率为1/2,测量后的态为
。因此,测量第二个量子比特的结果总是与测量第一个量子比特的结果相同。也就是说,测量结果是相关的。事实上,通过首先对第一个或第二个量子比特应用某些运算,可以在Bell态上进行其他类型的测量,而且在第一个量子比特和第二个量子比特的测量结果之间仍然存在有趣的相关性。而且Bell态下的测量相关性比经典系统之间存在的相关性更强。
更一般地,我们可以考虑一个有n个量子比特的系统。该系统的计算基态为
![]()
,这个系统的量子态是由
![]()
个振幅决定的。从原理上讲,大自然操纵着如此庞大的数据量,即使对于只有几百个原子的系统也是如此。这就好像大自然把
![]()
张隐藏的草稿纸放在一边,随着系统的发展,她在这些草稿纸上进行计算。这种巨大的潜在计算能力是我们非常想利用的。