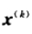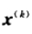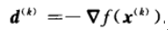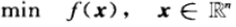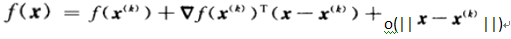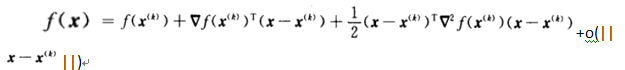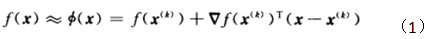本文由作者林洋港授权网易云社区发布。
一、 L-BFGS是什么
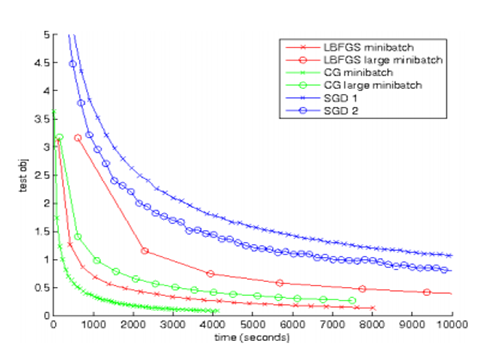
L-BFGS是解无约束非线性规划问题最常用的方法,具有收敛速度快、内存开销少等优点,在机器学习各类算法中常有它的身影。简单的说,L-BFGS和梯度下降、SGD干的同样的事情,但大多数情况下收敛速度更快,这点在大规模计算中很重要。下图是深度学习Autoencoder模型不同优化方法的比较。
二、 L-BFGS“之前”的那些方法
这里的“之前”并不是说L-BFGS问世之前就已经存在的方法,而是指为了更好的理解L-BFGS需要了解的其他方法。无约束问题定义:
我们先从泰勒展开开始,这可以说是本文介绍的所有方法的基础。f在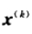
二阶泰勒展开为
去掉最后的余项,得到
2.1 最速下降法(Gradient descent)
CD算法的一个前提条件就是f在