本人刚开始接触深度学习,可以写一些简单的CNN网络,目前使用到的语言是python基础,搭配Pytorch框架,在一段时间内感到对深度学习的困惑,不知道进一步学习的方向。
在学习深度学习之前,无数的人告诉我,数学是学习深度学习的基础,不会就很麻烦,需要补。对于我个人来说,数学要是能学会,我又何必学习深度学习?于是各种尝试如何在数学基础一般的情况下,熟悉深度学习。
Don't BB ,show me the code!
就不!你咬我啊?
从CNN开始,不理解数学,硬写!写了一遍又一遍,把网络模型每一行都熟悉,抠除掉无关代码和核心框架,发现了网络模型的套路:
1、读取数据集,并进行数据预处理;
2、构建合适的网络模型,训练数据;
3、调用优化器(感知器),进行参数优化;
4、反向传播,更新参数,进行新一轮数据测试;
5、评估网络模型的准确率。
就在此时,看到了大神写的CNN,居然发现了其中可以优化的地方(PS:别问我为什么要优化,还不是因为设计的模型准确率不高、适应性不强):
首先可以优化的地方是参数:学习率、批数(btch_size),结果效果不怎么明显;
其次优化的是网络模型,涉及到的主要是网络模型的层数和激活函数,卷积层中可以设置的又主要是卷积核数、步长值、填充,激活函数主要是函数的选择上;
到此,一般的深度学习的科普工作就完成了,已经可以自己动手设计自己的网络模型了,有没有很兴奋?
那么,如果你目前没有深度学习的项目时,你就会迷茫,不知道下一步的工作在哪里。
经过一段时间的沉默,也是因为大神的指导,要想进一步优化,需要更改网络模型中常见函数的设置,即函数的优化。
在这,你有没有想明白为什么一开始说学习深度学习,要学习数学呢?
在这里,深度学习涉及到的数学知识就开始体现了,线代、概率、矩阵论、离散、运筹等等,各种预苦无泪啊,数学不好。
也许是运气太好了,我又遇见深度学习上的另一位大神,神说,对于计算机来说,数学是工具、是基础,那么对于数学来说,计算机也是工具、是基础。理解代码,就能理解数学。
在这样的指导下,再次回头去看自己写的代码,从中找到目前可以做的工作,对比激活函数的区别,进行网络模型优化:
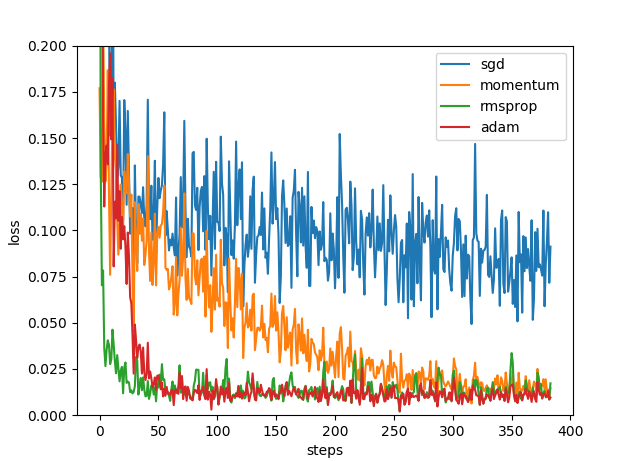
SGD(随机梯度下降):
Momentum(在SGD的基础上,加载梯度下降的动量):
RMSprop:
Adam:
然而,真正地,准确率更高的这些个网络模型的核心就是这里的区别,自己设计的激活函数和感知器。剩下的先不说了,给放个代码感受下最简单的感知器的设计:
# -*-coding:utf-8-*-
# 自定义SGN感知器
import numpy as np
a = 0.3
x = np.array([[1, 1, 3], [1, 2, 5], [1, 1, 8], [1, 2, 15], [1, 3, 7], [1, 4, 29]])
d = np.array([1, 1, -1, -1, 1, -1])
w = np.array([1, 0, 0])
def sgn(v):
if v >= 0:
return 1
else:
return -1
def comy(myw, myx):
return sgn(np.dot(myw.T, myx))
def neww(oldw, myd, myx, a):
pred = comy(oldw, myx)
print(oldw + a * (myd - pred) * myx)
return oldw + a * (myd - pred) * myx
for i in range(len(x)):
w = neww(w, d[i], x[i], a)
print("%d or %d" % (x[i][1], x[i][2]), comy(w, x[i]))
test1 = np.array([1, 9, 19])
print(comy(w, test1))
test = [1, 9, 64]
print(comy(w, test))
test=[1,5,11]
print(comy(w,test))
这其实就是一个机器学习的小例子,但是如你所愿,在没有学习太多数学的前提下,你已经完成了一小部分深度学习及其优化的问题。
分析上面的小例子,可以看出在每一步骤都可以找到一组优化后的参数组W,也了解了深度学习以矩阵为载体所进行的优化,那么我们接下来把自己做的以手写体和caifa10等数据集为数据源的卷积神经网络,我们尝试在过程中使用numpy包把多维数据变成一维数据进行计算,可以看到参数究竟是怎么优化的,所以当你自己再去设计网络模型的时候,就可以从底层设计感知器和激活函数了。
好吧,编不下去了,因为我的理解也就先到这了,如果对你有用,记得点个赞。