先将静态波函数展开为本征态的线性叠加：

我们再本节将会用之前求解的一维无限深势阱的波函数和量子谐振子的波函数进行线性叠加，深入理解叠加态的概念，并建立物体图像。

一维无限深势阱的叠加态（Superposition for a particle in a box）

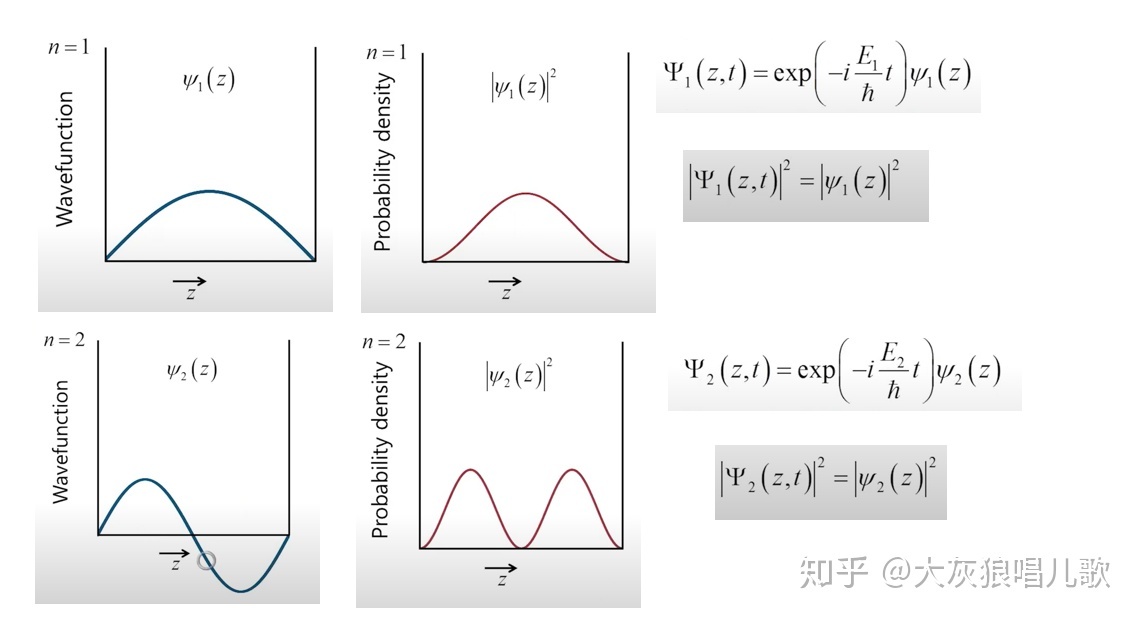
有一个无限深的势井，里面存在一个粒子，我们假设我们的解是第一能量本征值和第二能量本征值的线性叠加，且二者系数也相同，那么根据（9.1-1）式time-dependent 波函数有：

对应每一个本征函数我们都成对应的加入和时间有关的项，之后线性叠加。我们可以计算概率函数（probability density）

我们可以看到式（9.1-3）中

震荡的角频率只和能量的差值有关，而和能量的起始位置无关。那么接下来我们将类似的画出图1那样的概率密度分布图：

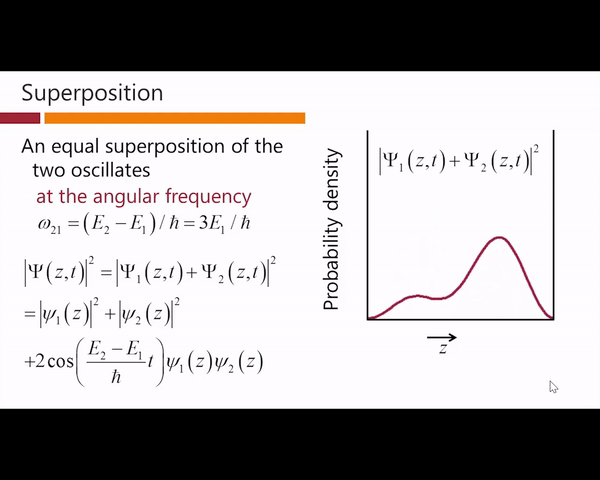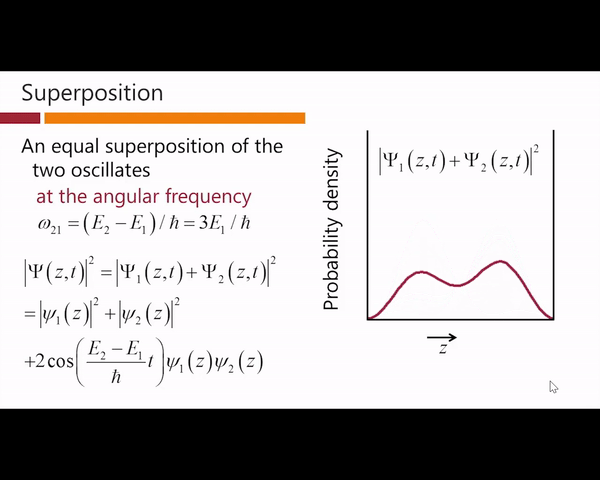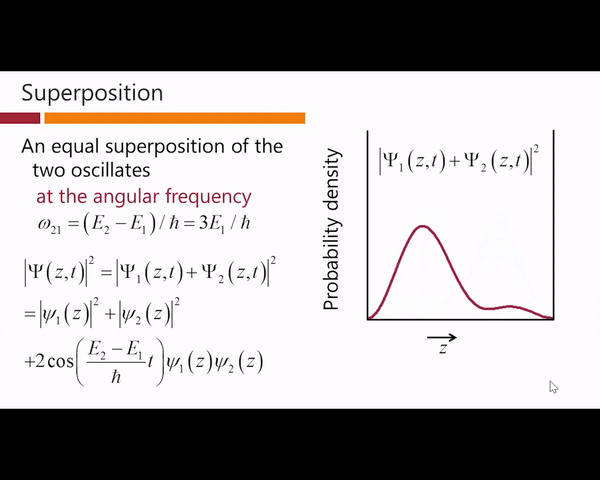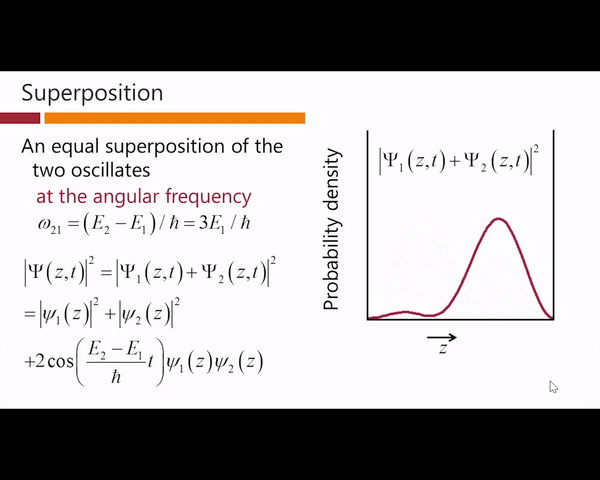
我们发现概率密度函数不再是一个常数，而是一个不断在震荡的函数，此时我们看到了和经典理论中的波动一样的，与时间有关的震荡，因此time-dependent波函数可以描述系统是如何随时间变化的。值得注意的是在量子力学中叠加态的额概率密度是

量子谐振子的叠加态（Superposition for the harmonic oscillator）

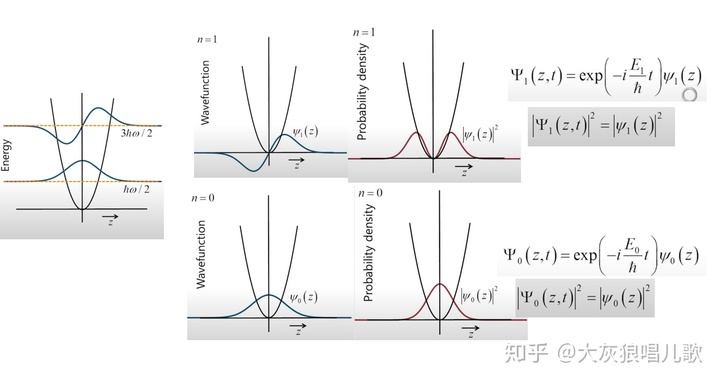
我们仍然去取能量最低的两个能量本征值

那么概率密度为：

该概率密度函数的图像为图4所示，其震荡频率为：

相干态（coherent state）

想干态的定义如下：In physics, specifically in quantum mechanics, a coherent state is the specific quantum state of the quantum harmonic oscillator, often described as a state which has dynamics most closely resembling the oscillatory behavior of a classical harmonic oscillator.

相干态是薛定谔1926年解释经典力学中的谐振子和量子力学中波函数的关系时提出的。我们加下来学习的相干态是1960年代罗伊·杰·格劳伯（Roy Glauber）提出的。Roy Glauber是现代激光量子力学和相干光的奠基人之一。他因对光学相干性的量子理论的贡献，而获得一半的2005年诺贝尔物理学奖。

对于一个频率为

其中

当N=1时，

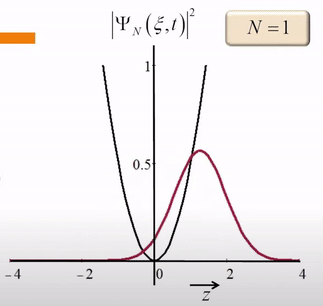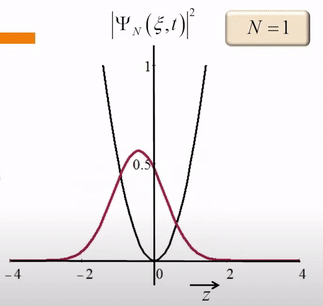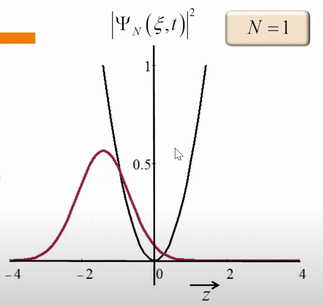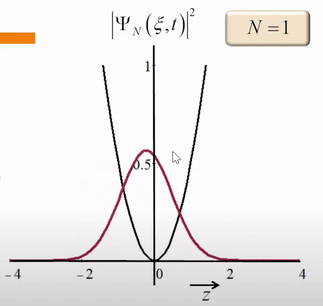
但这仍然不是经典力学中，一个小球在抛物线的势能中的运动。我们改变N的取值，可以看到

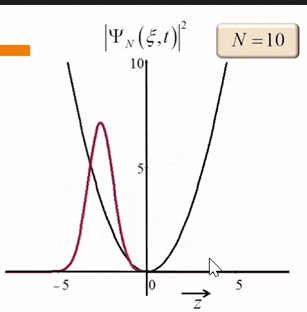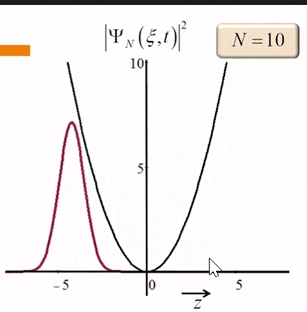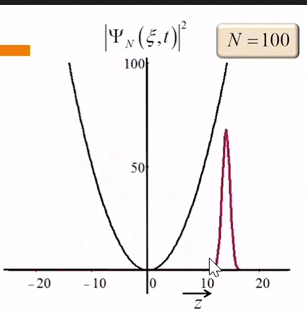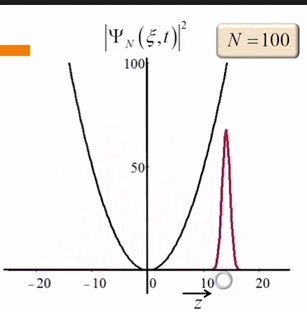
我们再来看一下无限深势阱中三个本征函数的等强度叠加，因为本征能量之间的差值不成固定比值，所以叠加态的波函数永远不会出现重复的分布：

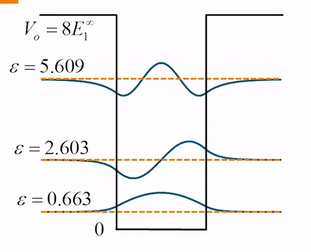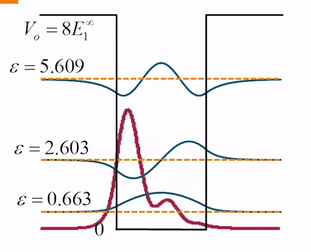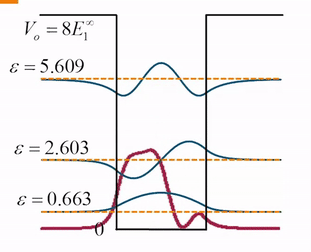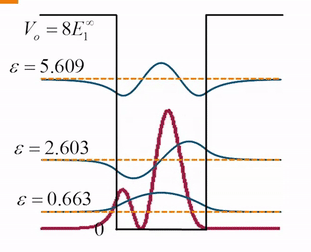
那么下一节，我们将讲解在自由空间运动的粒子如何用量子力学波函数的叠加态表示。