C语言数组
一、数组的概念
用来存储一组数据的构造数据类型
特点:只能存放一种类型的数据,如全部是int型或者全部是char型,数组里的数据成为元素。
二、数组的定义
格式: 类型 数组名[元素个数];
举例:存储5个人的年龄
Int agrs[5]; //在内存中开辟4x5=20个字节的存储空间
可以在定义数组的同时对数组进行初始化:
Int ages[5]={17,18,19,20,21};
遍历数组:
For(int i=0;i<5;i++)
{
Printf(“ages[%d]=%d\n”,i,ages[i]);
}
注意:
(1)数组的初始化
①. Int ages[5]={17,18,19,20,21};//一般写法
②. Int ages[5]={17,18};//只对前两个元素赋值
③. Int ages[5]={[3]=10,[4]=11};//对指定的元素赋值,这里为第三个和第四个
④. Int ages[]={11,12,13}.//正确,右边的元素确定,则个数可以省略这里为3个。
⑤. Int ages[];//错误,编译器无法知道应该分配多少的存储空间
⑥. Int ages[5];ages={17,18,19,20,21};//错误,只能在定义数组时这样进行初始化
⑦. Int ages[‘A’]={1,2,3};//正确,相当于是ages[65]
⑧. Int count=5;int ages[count];//如果不进行初始化,则这种写法正确,编译器不会报错为其分配20个字节的存储空间,ages[0]=1;ages[1]=2;可以像这样对数组的元素进行赋值,但是2,3,4等元素的值时不确定的。
⑨. 而int count=5;int ages[count]={1,2,3,4,5};//这种写法是错误的,在定义数组时对数组进行初始化,元素的个数必须为常量或者不写,不能是一个变量
(2)计算数组元素
当没有表明数组元素个数时,如何对其进行遍历(要求使用数组元素个数)?
可以使用sizeof运算符来计算数组元素的个数
Int count=sizeof(ages)/sizeof(int); //数组的总长度除以单个的长度等于元素个数
三、数组内存存储细节
假设有数组如下:
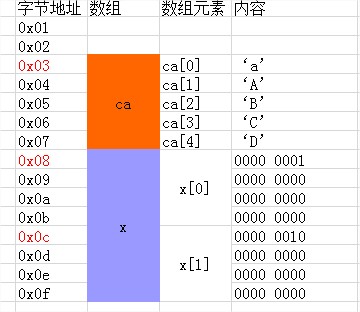
Int x[]={1,2};
Char ca[5]={‘a’,‘A’,‘B’,‘C’,‘D’};
数组名即代表数组的地址,数组的地址==数组名(ca)==数组的首元素的地址&ca[0]
在内存中,内存从大到小进行寻址,为数组分配了存储空间后,数组的元素自然的从上往下排列存储,整个数组的地址为首元素的地址。
模拟该数组的内存存储细节如下:
注意:字符在内存中是以对应ASCII值的二进制形式存储的,而非上表的形式。
在这个例子中,数组x的地址为它的首元素的地址0x08,数组ca的地址为0x03。
四、数组-传址调用
Void change(int array[]) //数组可以作为函数的形参,可以省略数组元素的个数
{
Array[0]=100;
}
Void change2(int a) //基本类型作为函数的形参
{
a=200;
}
Int main()
{
Int ages[5]={1,2,3,4,5};
Change2(ages[0]);
Change(ages);
Return 0;
}
Array数组与ages数组的地址一致,若以数组作为函数的参数,这种传递方式是传址调用,传递的是整个数组的地址,修改形参数组元素的值,就是修改实参的值。
当你把一个数组当做参数来传递时,它会看做是一个指针,在该函数体内使用sizeof运算符来计算数组的长度,得出的数值永远为8,而非数组的实际长度,因为任何类型的指针都占8个字节的存储空间。
提示:数组作为一个函数的参数时,如果函数体涉及到数组遍历等操作,通常把数组的实际元素个数也作为参数传递给函数。
如 void maxofarray(int array[],sizeof(ages)/sizeof(int)){....}
五、二维数组
Int ages[50];//数组能够存放50个int类型的数据
Int ages1[3][10];//数组能够存放3个数组,每个数组存放10个数值,共3x10=30个述职数值。
一个二维数组a,a包括两个一维数组a[0]和a[1],每个一维数组都包括三个元素。
使用场合:五子棋,俄罗斯方块等,
假设:
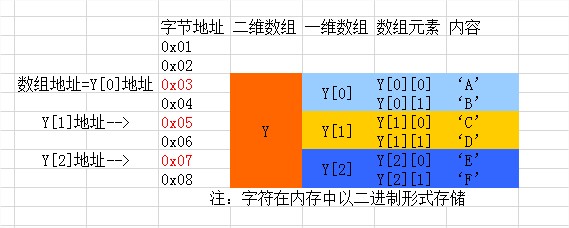
char Y[3][2]={
{‘A’,‘B’},
{‘C,‘D’},
{‘E,‘F’}
};
内存情况: