前言
尝试总结立体几何中常见几何体的建系类型,比如正四面体中、正三棱柱中、四棱锥等中的建系方法,坐标计算方法等,便于学习。
典例剖析
例1【正四面体中的建系】
如图,正四面体\(P-ABC\)中,\(D\)、\(E\)分别是\(AB\)和\(PC\)的中点,则直线\(AE\)与\(PD\)所成角的余弦值是多少?
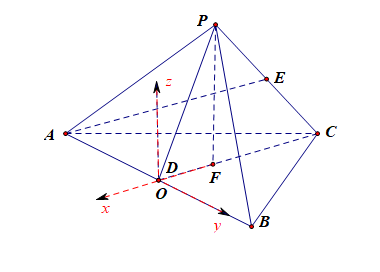
法1:空间向量法,如图所示,\(PF\perp\)面\(ABC\),\(F\)为\(\Delta ABC\)的中心,
以点\(D\)为坐标原点,以\(DF\)、\(DB\)以及与\(FP\)平行的直线分别为\(x\),\(y\),\(z\)轴建立如图所示的空间直角坐标系,
令正四面体的棱长为\(2\),则得到以下点的空间坐标
\(D(0,0,0)\),\(A(0,-1,0)\),\(B(0,1,0)\),
\(C(-\sqrt{3},0,0)\),\(P(-\cfrac{\sqrt{3}}{3},0,\cfrac{2\sqrt{6}}{3})\),\(E(-\cfrac{2\sqrt{3}}{3},0,\cfrac{\sqrt{6}}{3})\),
则有\(\overrightarrow{PD}=(\cfrac{\sqrt{3}}{3},0,-\cfrac{2\sqrt{6}}{3})\);\(\overrightarrow{AE}=(-\cfrac{2\sqrt{3}}{3},1,\cfrac{\sqrt{6}}{3})\);
令异面直线\(PD\)和\(AE\)的夹角为\(\theta\),则有\(cos\theta\)
\(=\cfrac{|\cfrac{\sqrt{3}}{3}\cdot (-\cfrac{2\sqrt{3}}{3})+0\cdot 1+(-\cfrac{2\sqrt{6}}{3}\cdot \cfrac{\sqrt{6}}{3})|}{\sqrt{(\cfrac{\sqrt{3}}{3})^2+(-\cfrac{2\sqrt{6}}{3})^2}\cdot \sqrt{(-\cfrac{2\sqrt{3}}{3})^2+1^2+(\cfrac{\sqrt{6}}{3})^2}}=\cfrac{2}{3}\)。
说明:向量的夹角范围为\([0,\pi]\),两异面直线的夹角范围\([0,\cfrac{\pi}{2}]\)。
法2:立体几何法,先作再证后算。
思路:异面直线所成的角,一般是经过平移,使其相交,构建三角形来计算。
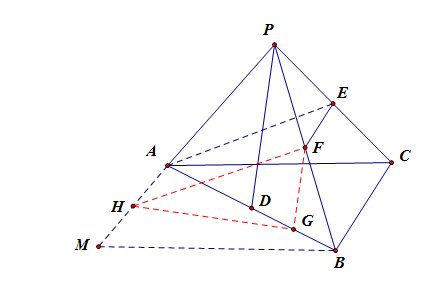
过点\(A\)做\(AM//BC\),过点\(B\)做\(BM//AC\)交\(AM\)于点\(M\),
点\(F\)、\(H\)、\(G\)分别是线段\(PB\)、\(AM\)、\(BD\)的中点,连接\(HF\)、\(FG\)、\(HG\),
则有\(EF//==AH\),则\(AE//FH\),又\(PD//FG\),故\(\angle HFG\)为两条异面直线所成的角。
设正四面体的棱长为\(2\),