前缀树及C++实现

文章目录

- - 前缀树

前缀树

1 什么是Trie树

Trie树，即前缀树，又称单词查找树，字典树，是一种树形结构，是一种哈希树的变种。典型应用是用于统计和排序大量的字符串（但不仅限于字符串），所以经常被搜索引擎系统用于文本词频统计。

Trie树的核心思想是空间换时间，利用字符串的公共前缀来降低查询时间的开销以达到提高效率的目的。它的优点是：最大限度地减少无谓的字符串比较，查询效率比哈希表高。

它有3个基本性质：

根节点不包含字符，除根节点外每一个节点都只包含一个字符。
从根节点到某一节点，路径上经过的字符连接起来，为该节点对应的字符串。
每个节点的所有子节点包含的字符都不相同。

2 树的构建与查询

根据一个例子来描述trie树的构建：
题目：给定100000个长度不超过10的单词，判断每一个单词是否出现过，如果出现过，给出第一次出现的位置。
思路：如果对每一个单词都遍历整个单词序列，那么时间复杂度就是 $O(n^2)$ ，单词序列的长度是100000，显然这样的时间复杂度代价太高了。但是考虑100000个单词肯定有一些字符串的重复，trie树，即前缀树来解决这个问题最恰当不过了。一个前缀树的形式是什么样的呢？
假设有abc，abd，bcd，efg，hii，那么我们构建如下一个树结构用于表示这些单词：

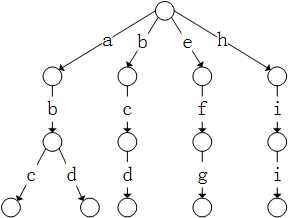
但是构造一个前缀树就是为了使遍历那些有相同的前缀的单词时更快速，目前这个多叉树上从根节点到叶节点每一条路径都是一个单词，如果我们增加了单词b，abcd两个单词呢，还是这样一条路走到黑，我们无法区分字母短的单词是否已经存储过，为了解决这个问题，我们可以在节点上记录信息，比如如果到达该字母后单词结尾，我们就在时候的节点上记录end+1，这样就可以知道有几个以该前缀结尾的单词，修改之后结构如下：

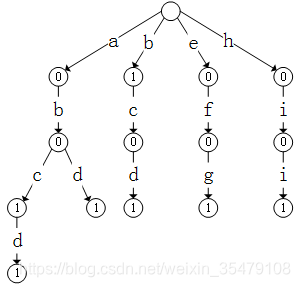
这是我们可以很明显看出来如最左边一条路径上，有一个单词是abc，一个单词是abcd。根据新添加的信息，我们可以知道所有字符串中有多少个该字符串，如果现在有另外一个问题，我想知道所有字符串中有多少个以该字符串作为前缀，那是不是得遍历该条路径后面的节点，将所有的end加起来。为了简单，我们仍然可以在节点中多存入一个信息，每个节点被划过了多少次，也就是在建立多叉树的时候就记录了以所有字符串中有多少个以某字符串作为前缀，划过的次数就是这个值。调整后结构如下：注：在C++实现部分，图中所有的S都加1，单词本身也是以他自己作为前缀的。

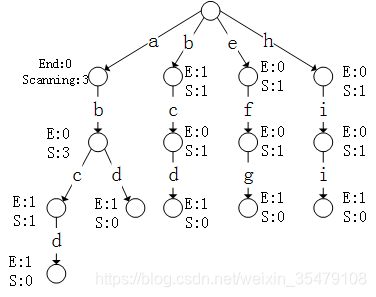
回到最初的题目，这样的结构可以根据节点的信息得到一个单词时候出现过（End>0），但是有一个要求我们没有满足，那就是如果存在这个单词我们如何返回这个单词在原来列表中的位置呢？根据前面介绍的多叉树结构的介绍，我想这个问题也很容易解决，节点中我们再多存入一些信息就可以，对于非结尾字符End=0，不需要存储其他的信息，对于结尾字符End>0，此时再存入信息，标注该单词在100000个单词词表中的位置，构建查询多叉树的时候就可以直接返回这个位置信息了。

3 Trie树的应用

除了本文引言处所述的问题能应用Trie树解决之外，Trie树还能解决下述问题（节选自此文：海量数据处理面试题集锦与Bit-map详解，说实话，作者总结的内容挺全的，但是总感觉乱七八糟的……吐槽是不对，我反省……）：

3、有一个1G大小的一个文件，里面每一行是一个词，词的大小不超过16字节，内存限制大小是1M。返回频数最高的100个词。
9、1000万字符串，其中有些是重复的，需要把重复的全部去掉，保留没有重复的字符串。请怎么设计和实现？
10、一个文本文件，大约有一万行，每行一个词，要求统计出其中最频繁出现的前10个词，请给出思想，给出时间复杂度分析。
13、寻找热门查询：搜索引擎会通过日志文件把用户每次检索使用的所有检索串都记录下来，每个查询串的长度为1-255字节。假设目前有一千万个记录，这些查询串的重复读比较高，虽然总数是1千万，但是如果去除重复和，不超过3百万个。一个查询串的重复度越高，说明查询它的用户越多，也就越热门。请你统计最热门的10个查询串，要求使用的内存不能超过1G。
(1) 请描述你解决这个问题的思路；
(2) 请给出主要的处理流程，算法，以及算法的复杂度。

4 C++实现Trie树，以及解决一些字符串问题

一个字符串类型的数组arr1，另一个字符串类型的数组arr2。

arr2中有哪些字符串，是arr1中出现的？请打印
arr2中有哪些字符串，是作为arr1中某个字符串前缀出现的？请打印
arr2中有哪些字符串，是作为arr1中某个字符串前缀出现的？请打印arr2中出现次数最大的前缀。

结果如图，具体实现在下面：

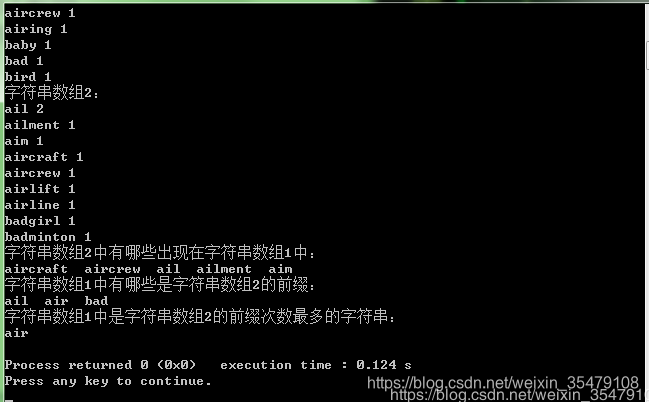
#include <iostream>
#include <string>
#include <string.h>

using namespace std;
const int MaxBranchNum = 26;//可以扩展

class TrieNode{
public:
    string word;
    int path;  //该字符被划过多少次，用以统计以该字符串作为前缀的字符串的个数
    int End; //以该字符结尾的字符串
    TrieNode* nexts[MaxBranchNum];

    TrieNode()
    {
        word = "";
        path = 0;
        End = 0;
        memset(nexts,NULL,sizeof(TrieNode*) * MaxBranchNum);
    }

};

class TrieTree{
private:
    TrieNode *root;
public:
    TrieTree();
    ~TrieTree();
    //插入字符串str
    void insert(string str);
    //查询字符串str是否出现过，并返回作为前缀几次
    int search(string str);
    //删除字符串str
    void Delete(string str);
    void destory(TrieNode* root);
    //打印树中的所有节点
    void printAll();
    //打印以str作为前缀的单词
    void printPre(string str);
    //按照字典顺序输出以root为根的所有单词
    void Print(TrieNode* root);
    //返回以str为前缀的单词的个数
    int prefixNumbers(string str);
};

TrieTree::TrieTree()
{
    root = new TrieNode();
}


TrieTree::~TrieTree()
{
    destory(root);
}

void TrieTree::destory(TrieNode* root)
{
    if(root == nullptr)
        return ;
    for(int i=0;i<MaxBranchNum;i++)
    {
        destory(root->nexts[i]);
    }
    delete root;
    root = nullptr;
}


void TrieTree::insert(string str)
{
    if(str == "")
        return ;
    char buf[str.size()];
    strcpy(buf, str.c_str());
    TrieNode* node = root;
    int index = 0;
    for(int i=0; i<strlen(buf); i++)
    {
        index = buf[i] - 'a';
        if(node->nexts[index] == nullptr)
        {
            node->nexts[index] = new TrieNode();
        }
        node = node->nexts[index];
        node->path++;//有一条路径划过这个节点
    }
    node->End++;
    node->word = str;
}

int TrieTree::search(string str)
{
    if(str == "")
        return 0;
    char buf[str.size()];
    strcpy(buf, str.c_str());
    TrieNode* node = root;
    int index = 0;
    for(int i=0;i<strlen(buf);i++)
    {
        index = buf[i] - 'a';
        if(node->nexts[index] == nullptr)
        {
            return 0;
        }
        node = node->nexts[index];
    }
    if(node != nullptr)
    {
        return node->End;
    }else
    {
        return 0;
    }
}

void TrieTree::Delete(string str)
{
    if(str == "")
        return ;
    char buf[str.size()];
    strcpy(buf, str.c_str());
    TrieNode* node = root;
    TrieNode* tmp;
    int index = 0;
    for(int i = 0 ; i<str.size();i++)
    {
        index = buf[i] - 'a';
        tmp = node->nexts[index];
        if(--node->nexts[index]->path == 0)
        {
            delete node->nexts[index];
        }
        node = tmp;
    }
    node->End--;
}

int TrieTree::prefixNumbers(string str)
{
    if(str == "")
        return 0;
    char buf[str.size()];
    strcpy(buf, str.c_str());
    TrieNode* node = root;
    int index = 0;
    for(int i=0;i<strlen(buf);i++)
    {
        index = buf[i] - 'a';
        if(node->nexts[index] == nullptr)
        {
            return 0;
        }
        node = node->nexts[index];
    }
    return node->path;
}
void TrieTree::printPre(string str)
{
    if(str == "")
        return ;
    char buf[str.size()];
    strcpy(buf, str.c_str());
    TrieNode* node = root;
    int index = 0;
    for(int i=0;i<strlen(buf);i++)
    {
        index = buf[i] - 'a';
        if(node->nexts[index] == nullptr)
        {
            return ;
        }
        node = node->nexts[index];
    }
    Print(node);
}

void TrieTree::Print(TrieNode* node)
{
    if(node == nullptr)
        return ;
    if(node->word != "")
    {
        cout<<node->word<<" "<<node->path<<endl;
    }
    for(int i = 0;i<MaxBranchNum;i++)
    {
        Print(node->nexts[i]);
    }
}

void TrieTree::printAll()
{
    Print(root);
}


int main()
{
    cout << "Hello world!" << endl;
    TrieTree trie;
    string str = "li";
    cout<<trie.search(str)<<endl;
    trie.insert(str);
    cout<<trie.search(str)<<endl;
    trie.Delete(str);
    cout<<trie.search(str)<<endl;
    trie.insert(str);
    cout<<trie.search(str)<<endl;

    trie.insert(str);
    cout<<trie.search(str)<<endl;

    trie.Delete("li");
    cout<<trie.search(str)<<endl;
    trie.Delete("li");
    cout<<trie.search(str)<<endl;
    trie.insert("lia");
    trie.insert("lic");
    trie.insert("liab");
    trie.insert("liad");
    trie.Delete("lia");
    cout<<trie.search("lia")<<endl;
    cout<<trie.prefixNumbers("lia")<<endl;

    return 0;
}