排序
(参考大话数据结构第9章,归并排序没有看,快速排序的优化部分没有看)
相关概念:
1.内排序与外排序:根据在排序过程中待排序的记录是否全部被放置在内存中分为内排序和外排序。本文讨论的7种排序算法都是内排序。
2.稳定性:能保证排序前两个相等的数据其在序列中的先后位置顺序与排序后它们两个先后位置顺序相同。即:如,如果Ai==Aj,Ai原来在Aj位置前,排序后Ai仍然是在Aj位置前
冒泡排序:
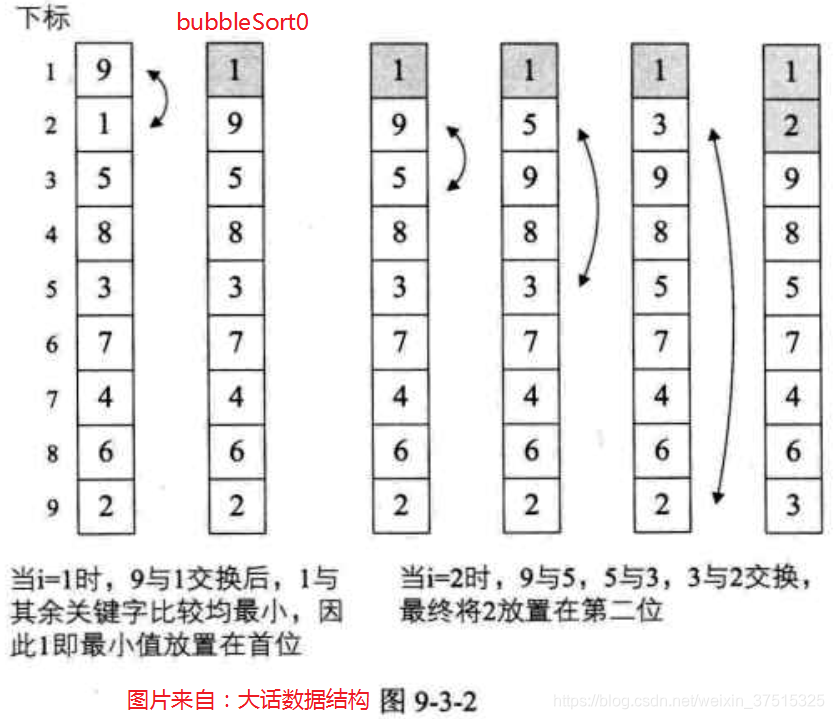
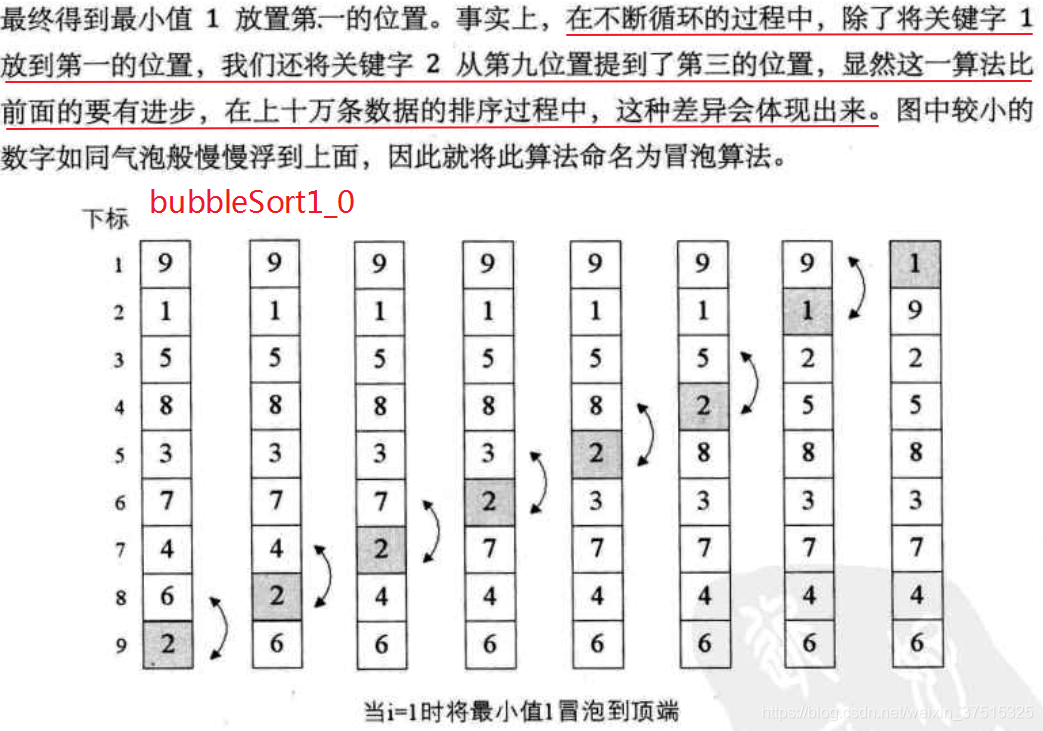
bubbleSort0:最基础版冒泡排序:j从前往后循环,j每循环一次只是将剩下数据中的最小值提到最前面
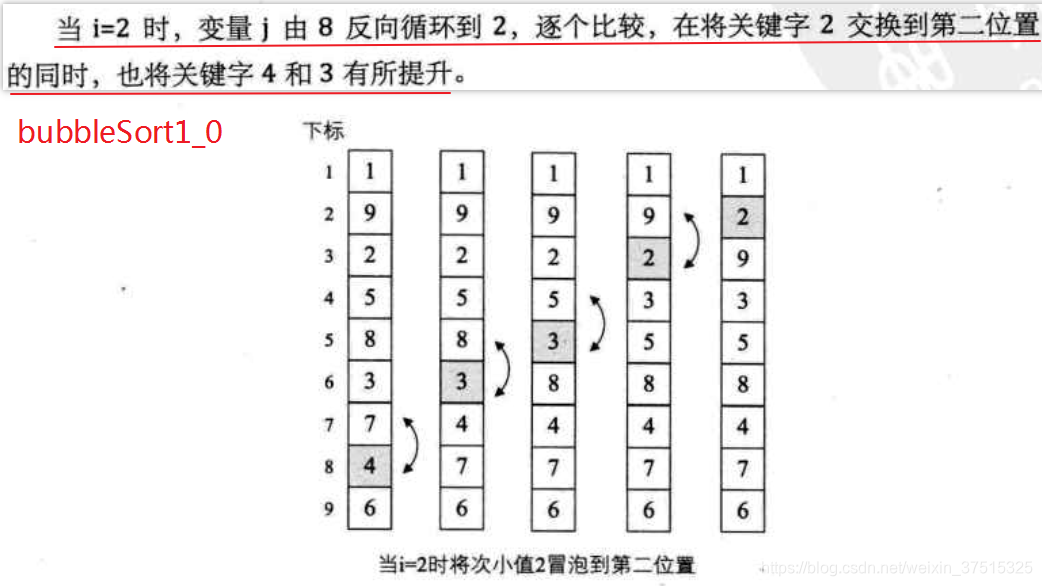
bubbleSort1:将bubbleSort0中的j从前往后循环变为j从后往前循环,
j每循环一次不仅将剩下数据中的最小值提到最前面,还将其他较小值的位置向前提,与bubbleSort0相比,降低了swap次数,但是比较的次数一样多
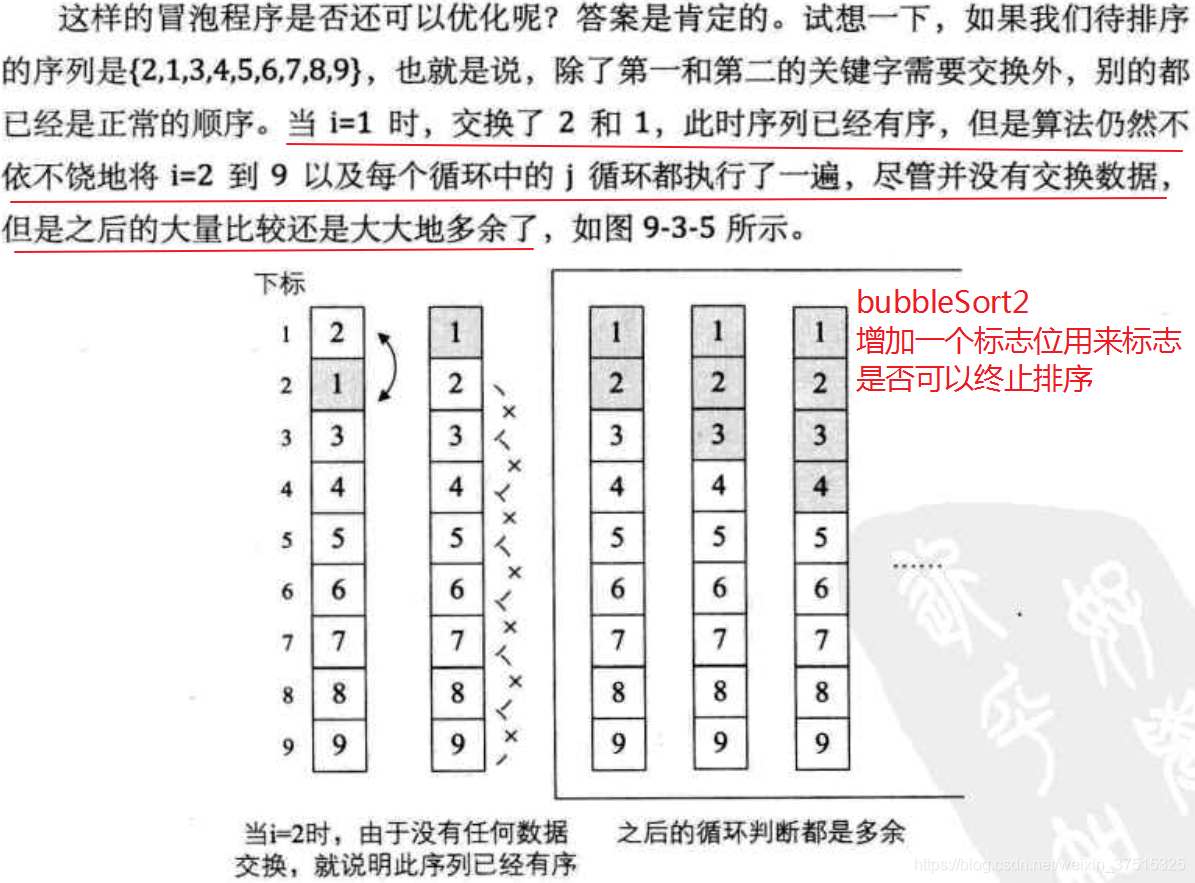
bubbleSort2:在bubbleSort1的基础上增加标志位,因为可能在bubbleSort1中的某个阶段就已经完成全部数据的排序,此时可以终止算法,不需要继续下去,相比于bubblesort1,swap次数一样多,降低了比较的次数
20210515:从分析来看,的确bubbleSort1比bubbleSort0好像好些,但我测试来看,同样的数据集,swap的次数一样多,但是bubbleSort2必须在bubbleSort1上才能实现。
20221030:在特定的场景下,bubbleSort2的确效率更高,但是bubbleSort0,bubbleSort1,bubbleSort2算法复杂度还都是O(n²)
C代码实现:
#define MAXSIZE 10
typedef struct{
int ele[MAXSIZE];//用于存储要排序数组
int length; //数组长度
}SqList;
void swap(SqList *L,int i,int j)
{
int temp = L->ele[i];
L->ele[i] = L->ele[j];
L->ele[j] = temp;
}
/****
bubbleSort0:最基础版冒泡排序:j从前往后循环,j每循环一次只是将剩下数据中的最小值提到最前面
bubbleSort1:将bubbleSort0中的j从前往后循环变为j从后往前循环,
j每循环一次不仅将剩下数据中的最小值提到最前面,还将其他较小值的位置向前提,与bubbleSort0相比,降低了swap次数,但是比较的次数一样多
bubbleSort2:在bubbleSort1的基础上增加标志位,因为可能在bubbleSort1中的某个阶段就已经完成全部数据的排序,此时可以终止算法,不需要继续下去
****/
/*默认按从小到大排列
最基础版冒泡排序*/
void bubbleSort0(SqList *L)
{
for(int i=0;i<L->length;i++)
{
for(int j=i+1;j<L->length;j++)
{
if(L->ele[j]<L->ele[i])
{
swap(L,i,j);
}
}
}
}
/*优化版1冒泡排序*/
void bubbleSort1(SqList *L)
{
for(int i=0;i<L->length;i++)
{
for(int j=L->length-2;j>=i;j--)
{
if(L->ele[j+1]<L->ele[j])//如果后面的比前面的小
{
swap(L,j+1,j);
}
}
}
}
/*优化版2冒泡排序*/
void bubbleSort2(SqList *L)
{
int flag = 1;//增加一个是否进行了swap操作的标志位
for(int i=0;i<L->length&&flag;i++)
{
for(int j=L->length-2;j>=i;j--)
{
flag = 0;//如果j循环一圈都没有swap,说明此时从i->j的部分数据已经按要求排序完成,不需要再排序了
if(L->ele[j+1]<L->ele[j])//如果后面的比前面的小
{
swap(L,j+1,j);
flag = 1;
}
}
}
}快速排序:是冒泡排序的优化。
20221030参考:对于快排讲的非常好!快速排序详解_凉夏y的博客-CSDN博客_快速排序
排序过程:
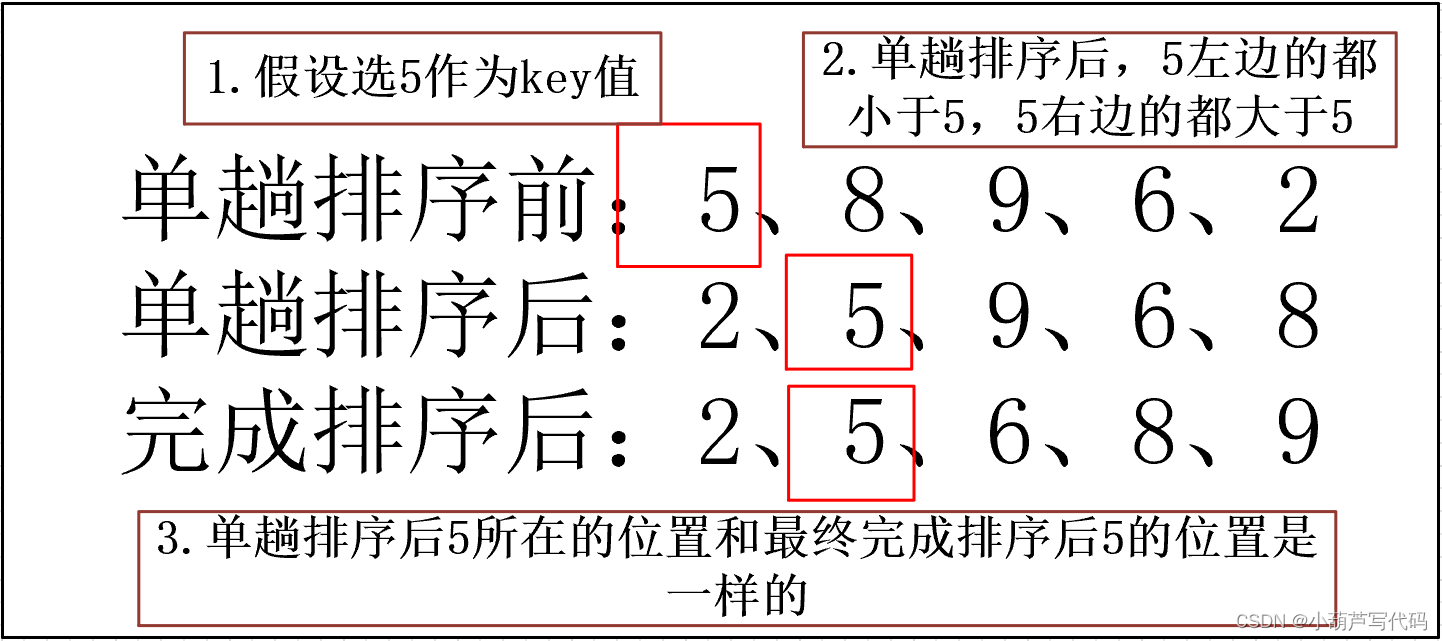
1.任选数组中的一个值作为key值,通过一次排序实现数组左边的部分比key小,右边的部分比key大,通过这样一次排序就把key值放在了最终排序完成应放在的位置上。所以这个过程是将key值放在了正确的位置上。
2.对上一次排序后左右两侧分割成两个数组,重复1的过程,直至分割后的数组只包含一个元素。整体排序完成。
单趟排序过程:
3.注意,如果key取最左边的值,要right先计算。如果key取最右边的值,要left先计算。这个原因是:当key取左边值,右边先动能保证left和right相遇时,相遇点的值是小于key的。如果取左边值为key值且left先动,这点无法保证。
3.注意,如果key取最左边的值,要right先计算。如果key取最右边的值,要left先计算。这个原因是:当key取左边值,右边先动能保证left和right相遇时,相遇点的值是小于key的。如果取左边值为key值且left先动,这点无法保证。切记切记!更深层的原因可以再分析下。
C代码实现:
static int swapCount = 0;
void swap(int arr[],int i,int j){
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
swapCount++;//记录swap次数
}
/*快排*/
/*partTwo 根据分割值key将数组分割成两部分,左部分为小于key的部分,右部分为大于key的部分*/
int partTwo(int arr[], int left, int right){
int key = arr[left];//取最左边为key值
printf("key = %d\n",key);
int pos_key = left;
while(left!=right){
//注意,如果key取最左边的值,要right先计算。如果key取最右边的值,要left先计算。
//这个原因是:当key取左边值,右边先动能保证left和right相遇时,相遇点的值是小于key的。如果取左边值为key值且left先动,这点无法保证。
while(left!=right&&arr[right]>=key) {right--;}
while(left!=right&&arr[left]<=key) {left++;}
swap(arr,left,right);
}
swap(arr,pos_key,left);
return left;
}
void quickSort(int arr[],int left,int right){
printf("left=%d,right=%d\n",left,right);
if(left<right){
int pos = partTwo(arr,left,right);
quickSort(arr,left,pos-1);
quickSort(arr, pos+1, right);
}
}
int main(void) {
printf("Hello World\n");
int arr[5] = {4,2,5,8,1};
quickSort(arr,0,4);
for(int i=0;i<5;i++){
printf("%d ",arr[i]);
}
return 0;
}算法复杂度:
对n个元素进行快速排序的过程构成一棵递归树,在这样的递归树中,每一层最多对n个元素进行划分,所花的时间为O(n)。当每次划分的两个子区间中的元素个数大致相等时,递归树高度为log2n,快速排序呈现最好情况,即最好情况下的时间复杂度为O(nlog2n)即O(nlogn)。
优化方向:
1.可以通过三数取中法或九数取中法获取较好的枢轴。
2.优化必要的交换。
3.优化小数组的排序方案。
4.优化递归操作。
简单选择排序:
通过n-i次关键字间的比较,从n-i+1个记录中选出关键字最小的记录,并和第i个数据交换。
与冒泡排序相比,冒泡是每比较一次发现顺序不对就立刻交换,而简单选择排序是比较一圈后选出最小(或最大)的,只交换一次。
C代码实现:
void selectSort(SqList *L)
{
for(int i=0;i<L->length;i++)
{
int min=i;
for(int j=i+1;j<L->length;j++)
{
if(L->ele[min]>L->ele[j]) {min=j;}//选出最小的
}
if(min != i) {swap(L,min,i);}
}
}堆排序:是对选择排序的优化。
堆是具有下列性质的完全二叉树:每个节点的值都大于或等于其左右孩子节点的值,称为大顶堆。
堆是具有下列性质的完全二叉树:每个节点的值都小于或等于其左右孩子节点的值,称为小顶堆。
进行从大到小排序,使用小顶堆。进行从小到大排序,使用大顶堆。
定义:将待排序的序列构造成一个大顶堆。此时整个序列的最大值就是根节点。将其移走,然后将剩下的n-1个节点重新构造成一个大顶堆,重复进行。
需要解决两个问题:
1.如何由一个无序序列构成一个大顶堆。
2.输出堆顶元素后,调整剩余元素称为一个新的堆
C代码实现:
#define MAXSIZE 10
typedef struct{
int ele[MAXSIZE];//用于存储要排序数组
int length; //数组长度
}SqList;
/*
前提:L中start_id->end_id除L->ele[start_id]都满足大顶堆,只是调整start_id到正确的位置
将顺序表L中start_id->end_id的部分调整成一个大顶堆,默认L中的元素按二叉树层序排序分布
start_id是一个有孩子的节点(至少有一个左孩子节点),根节点的id=1,节点id从1开始递增*/
void bigHeapAdjust(SqList *L,int start_id,int end_id)
{
int child_max_id = start_id*2;//完全二叉树性质,左孩子节点id = 对应父节点id*2,这里先假设左孩子节点是左右孩子节点中的最大值。
int temp = L->ele[start_id];
while(child_max_id<=end_id) //左孩子节点存在
{
if(child_max_id+1<=end_id) //右孩子节点存在
{
if(L->ele[child_max_id+1]>L->ele[child_max_id]) {child_max_id = child_max_id+1;} //取左右孩子节点的最大值给左孩子节点
}
if(temp>=L->ele[child_max_id]) //父节点的值大于子节点,大顶堆构建结束
{
break;
}
L->ele[start_id] = L->ele[child_max_id];//取子节点最大值给父节点
start_id = child_max_id;
child_max_id*=2;
}
L->ele[start_id] = temp;
}
void heapSort(SqList *L)
{
/*将L中的元素构造成一个大顶堆*/
for(int i=L->length/2;i>0;i--)
{
bigHeapAdjust(L,i,L->length);//i=L->length/2意味着从堆中最后一个有子节点的父节点开始构造,直至根节点
}
for(int i=L->length;i>1;i--)
{
swap(L,1,i);
bigHeapAdjust(L,1,i-1);
}
}
int main()
{
SqList test;
/*注意,这里的数组从id=1开始存,而不是从id=0开始存,因为堆中的根节点id是从1开始的,对应起来bigHeapAdjust处理会很方便*/
test.length = 9;
test.ele[1] = 50;
test.ele[2] = 10;
test.ele[3] = 90;
test.ele[4] = 30;
test.ele[5] = 70;
test.ele[6] = 40;
test.ele[7] = 80;
test.ele[8] = 60;
test.ele[9] = 20;
heapSort(&test);
for(int i=1;i<10;i++)
{
ADI_PRINT("i=%d,data=%d\n",i,test.ele[i]);
}
return SUCCESS;
}直接插入排序:
将一个记录插入到已经排好序的有序表中,从而得到一个新的、记录数量增加1的有序表。
C代码实现:
void insertSort(SqList *L)
{
/*从i=1开始排序(第0个元素是已经排好序的)*/
int i,j;
for(i=1;i<L->length;i++)
{
if(L->ele[i]<L->ele[i-1])
{
int temp = L->ele[i];
for(j=i;temp<L->ele[j-1]&&j>0;j--)
{
L->ele[j] = L->ele[j-1];/*记录不断后移*/
}
L->ele[j] = temp;
}
}
}
int main()
{
SqList test;
test.length = 6;
test.ele[0] = 1;
test.ele[1] = 2;
test.ele[2] = 4;
test.ele[3] = 6;
test.ele[4] = 3;
test.ele[5] = 5;
insertSort(&test);
for(int i=0;i<test.length;i++)
{
ADI_PRINT("i=%d,data=%d\n",i,test.ele[i]);
}
return SUCCESS;
}希尔排序(缩小增量排序):是直接插入排序的优化。
步骤如下:
1.确定希尔增量(分组间隔),这个值没有要求,初始值通常使用待排序长度的一半(这种增量称为希尔增量)。
根据希尔增量分组,进行组内排序(使用插入排序)。
2.将希尔增量/2,再次进行分组,排序。
3.重复上述过程,直至希尔增量变为1,相当于对全组进行一次插入排序。
原理:
1.直接插入排序对基本有序的数据操作时,效率高,可以达到线性排序的效率。
2.直接插入排序对于数据量很少时,效率也很高。
希尔排序通过增量将待排序数据转化为数据量较小的多组数据,利用上述的第二点。不断缩小增量使得整体数据趋于有序态,利用上述第1点,达到效率较高。
C代码实现:
void shellSort(SqList *L)
{
int gap=L->length/2;//增量使用希尔增量,也可以使用其他增量如大话数据结构使用的是:gap = leng/3+1; gap更新也不是除2,而是gap=gap/3+1。
int i,j;
while(gap>=1)
{
for(i=gap;i<L->length;i++)
{
if(L->ele[i]<L->ele[i-gap])
{
int temp = L->ele[i];
for(j=i-gap;j>=0 && temp<L->ele[j];j=j-gap)
{
L->ele[j+gap] = L->ele[j];
}
L->ele[j+gap] = temp;
}
}
gap=gap/2;
}
}
int main()
{
SqList test;
test.length = 9;
test.ele[0] = 83;
test.ele[1] = 29;
test.ele[2] = 30;
test.ele[3] = 5;
test.ele[4] = 99;
test.ele[5] = 34;
test.ele[6] = 12;
test.ele[7] = 66;
test.ele[8] = 88;
shellSort(&test);
for(int i=0;i<test.length;i++)
{
ADI_PRINT("i=%d,data=%d\n",i,test.ele[i]);
}
return SUCCESS;
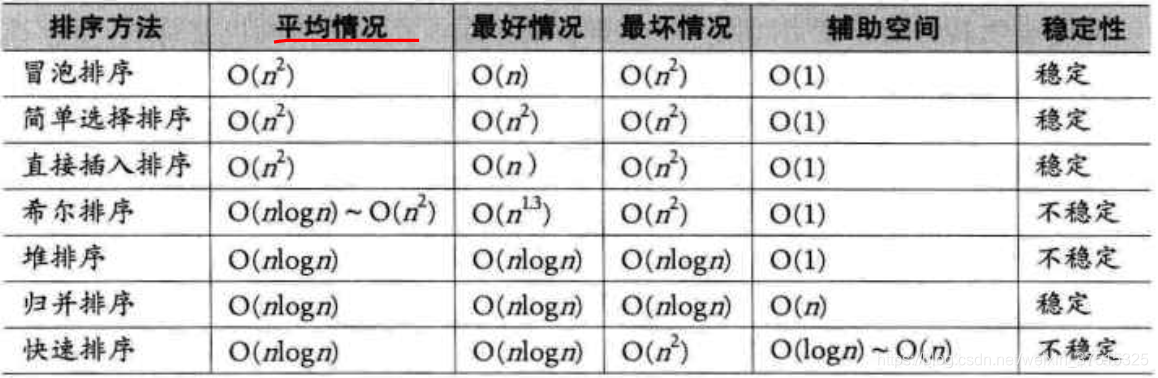
}算法复杂度分析:
注意分析包含数据比较和数据移动两个方面。
冒泡排序:使用最后优化过的代码分析:
最好情况(数据原本就是递增的):只需要n-1次比较,不需要数据移动。
最差情况(数据严格递减):需要1+2+3....+n-1=n(n-1)/2次比较,等数量级的数据移动(这里的数据移动指的是调用swap做数据交换)。
所以,复杂度O(n2)。
简单选择排序:最大特点就是数据移动次数相当少。
无论最好最差情况:比较的次数都是n(n-1)/2。
最好情况:交换是0次。最差情况,交换是n-1次。
所以,复杂度O(n2)。性能上略优于冒泡排序。
直接插入排序:
最好:只需n-1次比较,不需要移动数据。
最差:需要比较2+3+.....+n=(n+2)(n-1)/2,移动:3+4+....n+(n+1)=(n+4)(n-1)/2
(这里的移动和冒泡排序不一样,冒泡中的是做数据交换,交换一次相当于3次数据移动)
算法复杂度O(n2),性能优于冒泡排序和选择排序。
希尔排序:
O(nlogn)--O(n2) 最好O(n1.3) 最差O(n2) 与使用的增量有关。使用希尔增量最坏的时间复杂度是O(n2)。
堆排序:
时间复杂度O(nlogn)。堆对原始记录的排序状态并不敏感,所以无论是最好、最坏和平均时间复杂度都是O(nlogn)。
由于构建初始堆需要的比较次数比较多,堆排序不适合待排序序列个数比较少的情况。
快速排序:
最好情况是枢轴每次都能均匀划分序列,算法复杂度O(nlogn)
最坏情况是枢轴为最大或最小数字,算法复杂度O(n2)
平均复杂度O(nlogn)
对于快速排序时间复杂度的分析,可以看这篇文章:https://www.cnblogs.com/fengty90/p/3768827.html
个人理解:最好时间复杂度:递归为logn次,每次partTwo要进行n次比较,时间复杂度:O(nlogn)
最差时间复杂度:递归为n次,时间复杂度: O(n2)