论文:Point Feature Extraction on 3D Range Scans Taking into Account Object Boundaries
论文阅读
- 摘简介
- 使用点云生成的距离图像
- 提取了前景到背景的边界
- 使用NARF特征,提出了3维数据的特征点和描述符提取方法
<1>:特征点需要所在平面稳定(具有稳定的法线)
<2>:利用局部视图中的物体边界(因为物体边界是特殊的,边界的特征点和描述符会使整个过程更加具有鲁棒性),提出了一种边界提取方法
- border extraction(边界提取)
-
可以将边界分为三个类型:object borders(物体边界)、shadow borders(遮挡边界),veil points(过渡边界)
-
过渡边界是3D距离中一种特征,可以提高匹配精度和分类效果
-
使用两个指标提取边界区域:法线变化、锐角、相邻点之间的距离变化(对于噪声和分辨率具有非常强的鲁棒性)
-
对于距离图像中的每一个点和其邻域进行如下操作:
<1> :使用启发式方法,计算不穿过边界的邻域点的距离值
<2> :计算评分:用来描述点为边界的可能性
<3> :区分边界点的类型
<4> :使用非极大值抑制找到准确的边界位置 -
启发式算法
某个点的所有2d邻域点,对应3d距离位于同一平面的点
p i p_i pi距离图像中的某一像素点
{ n 1 , . . . , n s 2 } : \{n_1,...,n_{s^2}\}: {n1,...,ns2}:像素 p i p_i pi为中心点的邻域点集,大小为S×S
{ d 0 , . . . , d s 2 } : \{d_0,...,d_{s^2}\}: {d0,...,ds2}:邻域点对应的3D距离
{ d 0 ′ , . . . , d s 2 ′ } : \{d'_0,...,d'_{s^2}\}: {d0′,...,ds2′}:按增量顺序排序的,邻域点对应的3D距离
M : M: M:表示领域点内与像素点 p i p_i pi位于同一平面的点的最少个数
δ = d M ′ \delta=d'_M δ=dM′:表示代表性距离( p i − s p_i-s pi−s,不包含越界点)
文章中 S S S=5, M = ( ( s + 1 ) 2 ) 2 = 9 M=(\frac{(s+1)}{2})^2=9 M=(2(s+1))2=9,具有最大值M的点,意味该点位于直角点 -
计算可信度/评分
计算四个方向具有边界的可能性(向上、向下、向左、向右):
以向右为例:
其右侧3维平均距离为:
P x , y : P_{x,y}: Px,y:表示深度图像在x,y的点
m p : m_p: mp:表示右侧用来计算点的个数,论文中为3
p r i g h t = 1 m p ∑ i = 1 m p p x + i , y p_{right}=\frac{1}{m_p}\sum_{i=1}^{m_p}p_{x+i,y} pright=mp1i=1∑mppx+i,y
使 p r i g h t p_{right} pright作为右邻域点,计算偏移:
d r i g h t = ∣ ∣ p x , y − p r i g h t ∣ ∣ d_{right}=||p_{x,y}-p_{right}|| dright=∣∣px,y−pright∣∣
使用 d r i g h t ∈ [ 0 , 1 ) d_{right}\in[0,1) dright∈[0,1)和 δ \delta δ计算评分,分数越高具有边界可能性越高:
s r i g h t = m a x ( 0 , 1 − δ d r i g h t ) s_{right}=max(0,1-\frac{\delta}{d_{right}}) sright=max(0,1−drightδ) -
平滑去除噪声 (略)
-
区分边界类型
通过判断距离值实现:
p x , y p_{x,y} px,y一个像素点
{ 物 体 边 界 p x , y < p r i g h t 遮 挡 边 界 p x , y > P r i g h t \begin{cases} 物体边界&p_{x,y}<p_{right}\\ 遮挡边界&p_{x,y}>P_{right}\\ \end{cases} {物体边界遮挡边界px,y<prightpx,y>Pright
对于所有可能为边界点的 P x , y P_{x,y} Px,y,查找其右边对应的遮挡边界:
在2D(x,y)像素邻域内(论文中文为3),找到评分做高的值,作为 s s h a d o w s_{shadow} sshadow,轻微的减小 s r i g h t s_{right} sright,如下:
s r i g h t ′ = m a x ( 0.9 , 1 − ( 1 − s s h a d o w ) 3 ) ∗ s r i g h t s'_{right}=max(0.9,1-(1-s_{shadow})^3)*s_{right} sright′=max(0.9,1−(1−sshadow)3)∗sright
再检查 s r i g h t ′ > 0.8 s'_{right}>0.8 sright′>0.8,且为相邻点 p x − 1 , y p_{x-1,y} px−1,y和 p x + 1 , y p_{x+1,y} px+1,y的最大值:将 p x , y p_{x,y} px,y标记为物体边界,并标记对应遮挡边界,将遮挡边界与物体边界之间的区域标志为过渡区域。
最后得到效果如下:
- interest point extraction(兴趣/特征点提取)
-
作用:减少搜索空间使特征提取聚焦于重要的点中
-
对于兴趣点的指标:
<1>: 必须考虑到边界和平面结构信息
<2>: 对与一个视点从不同的视度均可以提取到(兴趣点在各个方向上均有明显变化)
<3>: 具有稳定的法线或者相应的描述符可计算 -
计算步骤
<1> :遍历图像上的每一点,得到平面变化程度的评分(包含边界信息):曲率
<2> :计算图像每一个点的周围的主要方向,得到一个兴趣值(指标<1>),计算这些兴趣值之间的差异(指标<2>)、计算点所在局部平面的变化程度(指标<3)
<3> :对兴趣值进行平滑处理
<4> :执行非最大抑制找到兴趣点
上述过程中,最重要的指标为,支撑半径: σ \sigma σ,用来计算主导方向的兴趣值,与用来计算描述符需要考虑点的范围值相同,该值与想找到几何尺寸相关,值越大计算越大,特征越稳定,但是如果用来识别物体,该值越小越好,避免部分遮挡的影响,通常该值取待识别物体尺寸的0.25,如果识别大小不同的物体,需要使用多尺度。 -
注意事项
从之前的步骤,已知每一个点的上下左右的边界,对每一个边界像素仪45度步长对边界方向进行编码,
×通过计算邻域多个边界点的平均值可以减少误差
×应为距离图像为球坐标系下的值,在进行2D可视化时会失真,因此文中使用局部法线值(采用2D局部邻域内的像素点,使用PCA降维得到,忽略3D距离大于2 δ ( 边 界 估 计 时 的 参 数 ) \delta(边界估计时的参数) δ(边界估计时的参数)与的点)。 -
<1> :细节
表面变化与边界无关,对于每个点计算其邻域内的主曲率,得到其曲率的主方向和最大特征值。
图像中每一个点都会得到一个主方向向量 v v v:是边界点的主方向或者非边界点的主方向,
这些方向点的权重和为1,相对于其他点的权重为 1 − ( 1 − λ ) 3 1-(1-\lambda)^3 1−(1−λ)3 -
当有足够的点,在三维直径 σ \sigma σ内,有足够的点,该结果对分辨率、视距和非均匀点分布保持不变,
-
<2>
-
对于每一个像素上的点p;
其邻域值为 { n 0 , . . . , n N } ( 距 离 小 于 0.5 σ ) \{n_0,...,n_N\}(距离小于0.5\sigma) {n0,...,nN}(距离小于0.5σ),且邻域内的点没有边界点;
每个点 n i n_i ni,有一个主方向 v n i v_{ni} vni,权重 w n i w_{n_i} wni,为了减少来自于法线估计的噪声,将方向向量映射到与(像素点P与传感器位置连线之间构成的直线垂直)平面,对于每个 n i n_i ni我们都会得到一个一维角度 a n i a_{n_i} ani
由于两个相反的向量不能确定唯一的位置,且主曲率也不能分析得到唯一的方向,文中采用如下方式得到位移的角度:
α ′ = { 2 ∗ ( α − 180 ° ) α > 90 ° 2 ∗ ( α + 180 ° ) α < = − 90 ° \alpha'=\begin{cases} 2*(\alpha-180°) &\alpha>90°\\ 2*(\alpha+180°) &\alpha <=-90° \end{cases} α′={2∗(α−180°)2∗(α+180°)α>90°α<=−90°
得到效果图如下:
-
<3>
使用有界高斯核平滑角度和权重
得到点 p p p兴趣点 I p I_p Ip如下,将超过阈值 I I I的值作为兴趣点:
I 1 ( p ) = m i n i ( 1 − w n i m a x ( 1 − 10 ∗ ∣ ∣ p − n i ∣ ∣ σ , 0 ) ) f ( n ) = w n ( 1 − ∣ 2 ∗ ∣ ∣ p − n ∣ ∣ σ ∣ − 0.5 ) I 2 ( p ) = m a x i , j ( f ( n i ) f ( n j ) ( 1 − ∣ c o s ( α n i ′ − α n j ′ ) ∣ ) ) I ( p ) = I 1 ( p ) ∗ I 2 ( p ) I_1(p)=min_{i}(1-w_{n_i}max(1-\frac{10*||p-n_i||}{\sigma},0))\\ f(n)=\sqrt{w_n(1-|\frac{2*||p-n||}{\sigma}|-0.5)}\\ I_2(p)=max_{i,j}(f(n_i)f(n_j)(1-|cos(\alpha'_{n_i}-\alpha'_{n_j})|))\\ I(p)=I_1(p)*I_2(p) I1(p)=mini(1−wnimax(1−σ10∗∣∣p−ni∣∣,0))f(n)=wn(1−∣σ2∗∣∣p−n∣∣∣−0.5)I2(p)=maxi,j(f(ni)f(nj)(1−∣cos(αni′−αnj′)∣))I(p)=I1(p)∗I2(p)
I 1 : I_1: I1:可以提取具有高权重的的点值/平面剧烈变化
I 2 : I_2: I2:可以提取又有一对相邻点的主方向具有剧烈变化的点
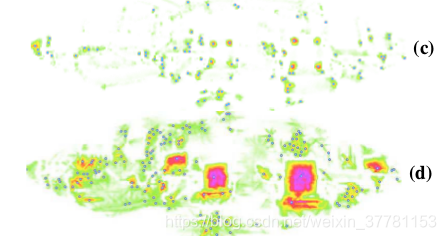
下图具有不同的 σ 值 \sigma值 σ值
下图中十字符号表示一个兴趣点位置。
- NARF 描述子
-
用来有效比较两个兴趣点的相似度
-
作用
<1> 利用被占空间和自由空间描述物体表面和物体轮廓
<2> 使位置点具有鲁棒性(缩放旋转)
<3> 为提取点提供了独特的局部坐标系
<4> 机器人的滚动不变性可能会不必要地增加搜索空间的大小,因为机器人大部分时间都会以零滚动角运行。NARF描述符使我们能够在正常情况下提取一个独特的方向 -
计算兴趣点的NARF步骤
<1> 锁定视角:计算出距离图像上某点一个法向对齐距离值的局部平面,并沿法相方向观察该点(我认为是切平面)
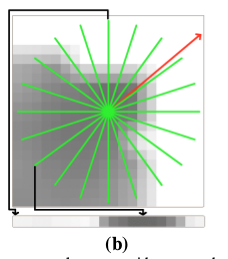
<2> 在该面片上覆盖一个星形图案,其中每个光束对应于最终描述符中的一个值
<3> 它捕捉光束变化下像素的大小,从描述符中提取唯一的方向 (可选)
<4> 并根据该值(方向)移动描述符,使其对旋转保持不变 (可选) -
计算对齐平面
1)采用局部坐标系:以兴趣点为原点,z轴指向法向量,y轴根据世界坐标系中的垂直向量定向,将位于支撑半径 σ / 2 \sigma/2 σ/2内的所有点映射到该平面
2)x,y,z坐标系就是描述符单元的坐标系,一个cell的值为所有映射点中,z值最小的,没有3D点映射的cell为 0.5 σ 0.5\sigma 0.5σ
3)法线计算:PCA计算所有点,确保描述符具有最大的稳定性
4)图像块(用来计算法线):大小应当适中,过大会导致结构失真,也不能过小超过分辨率,一般选用10×10大小
5)高斯差值:防止在原始扫描分辨率较低的部分失真
6)将具有n(一般n=36,每束光之间的差值为 10 ° 10\degree 10°)束星形投影到兴趣点所在的局部坐标,每束光 b i b_i bi对应一个网格的点集 { c 0 , . . . , c m } \{c_0,...,c_m\} {c0,...,cm}( c 0 c_0 c0为块的中间值,其余值按到 c 0 c_0 c0的距离排序)
7)第i个光束的描述符 D i D_i Di为w ( c j ) : w(c_j): w(cj):权重,块中间权重为2
w ( c j ) = 2 − 2 ∗ ∣ ∣ c j − c 0 ∣ ∣ σ w(c_j)=2-\frac{2*||c_j-c_0||}{\sigma} w(cj)=2−σ2∗∣∣cj−c0∣∣
D i ′ D'_i Di′:几何意义离中心越近,表面的变化越大,变化越强烈,值越偏离0
D i ′ = ∑ j = 0 m − 1 ( w ( c j ) ( c j + 1 − c j ) ) ∑ j = 0 m − 1 w ( c j ) D'_i=\frac{\sum^{m-1}_{j=0}(w(c_j)(c_{j+1}-c_j))}{\sum_{j=0}^{m-1}w(c_j)} Di′=∑j=0m−1w(cj)∑j=0m−1(w(cj)(cj+1−cj))
D i D_i Di:将 D i ′ D'_i Di′归一化到 [ − 0.5 , 0.5 ] [-0.5,0.5] [−0.5,0.5]
D i = a t a n 2 ( D i ′ , σ 2 ) 180 ° D_i=\frac{atan2(D_i',\frac{\sigma}{2})}{180°} Di=180°atan2(Di′,2σ)
最后得到了下图b(可视化描述符),左边箭头指向的网格具有低值(白色),右边箭头网格有较高值(黑色)
8)旋转不变性:将得到的描述符(360度)离散化为直方图,每个 β \beta β方向的单元格对应值如下:选择其中最大值作为主方向,并保存其中超过主方向 0.8 0.8 0.8倍的作为副方向
γ i : \gamma_i: γi:角度方向上的第i个描述网格
h ( β ) = 0.5 + 1 2 ∑ i = 1 n D i ( 1 − ∣ β − γ i ∣ 180 ° ) 2 h(\beta)=0.5+\frac{1}{2}\sum_{i=1}^nD_i(1-\frac{|\beta-\gamma _i|}{180°})^2 h(β)=0.5+21i=1∑nDi(1−180°∣β−γi∣)2
9)描述符匹配:使用曼哈顿距离除以描述符中的单元数,这将距离标准化为[0,1]中的值,得到图c:
- 验证旋转不变性、匹配效果、时间(略)
使用
- 核心代码
pcl::RangeImageBorderExtractor BEXT; //边缘提取容器
pcl::RangeImage& range_image = *rangeimage_ptr;
BEXT.setRangeImage(&range_image);
- 具体使用
#include <iostream>
#include <boost/thread/thread.hpp>
#include <pcl/range_image/range_image.h>
#include <pcl/io/pcd_io.h>
#include <pcl/visualization/range_image_visualizer.h>
#include <pcl/visualization/pcl_visualizer.h>
#include <pcl/features/range_image_border_extractor.h>
#include <pcl/console/parse.h>
#include <pcl/visualization/common/float_image_utils.h>
#include <pcl/io/png_io.h>
#include <pcl/point_types.h>
#include <pcl/io/ply_io.h>
#include <pcl/filters/statistical_outlier_removal.h>
using namespace std;
using namespace pcl;
#define PointType pcl::PointXYZRGB
boost::shared_ptr<pcl::visualization::PCLVisualizer> RGB_viwer(pcl::PointCloud<pcl::PointXYZ>::Ptr cloud,
pcl::PointCloud<pcl::PointWithRange>::Ptr cloud1,
pcl::PointCloud<pcl::PointWithRange>::Ptr cloud2,
pcl::PointCloud<pcl::PointWithRange>::Ptr cloud3){
boost::shared_ptr<pcl::visualization::PCLVisualizer> viewer(new pcl::visualization::PCLVisualizer("3D Viewer"));
int v1(0);
viewer->addPointCloud<pcl::PointXYZ>(cloud,"simple cloud");
//设置点云属性
viewer->setPointCloudRenderingProperties(pcl::visualization::PCL_VISUALIZER_POINT_SIZE,1,"simple cloud");
pcl::visualization::PointCloudColorHandlerCustom<pcl::PointWithRange> single_color1(cloud1,0,255,0);
viewer->addPointCloud<pcl::PointWithRange>(cloud1,single_color1,"XYZ add color1");
viewer->setPointCloudRenderingProperties(pcl::visualization::PCL_VISUALIZER_POINT_SIZE,3,"XYZ add color1");
int v2(1);
pcl::visualization::PointCloudColorHandlerCustom<pcl::PointWithRange> single_color2(cloud2,255,0,0);
viewer->addPointCloud<pcl::PointWithRange>(cloud2,single_color2,"XYZ add color2");
viewer->setPointCloudRenderingProperties(pcl::visualization::PCL_VISUALIZER_POINT_SIZE,3,"XYZ add color2");
int v3(2);
pcl::visualization::PointCloudColorHandlerCustom<pcl::PointWithRange> single_color3(cloud3,0,0,255);
viewer->addPointCloud<pcl::PointWithRange>(cloud3,single_color3,"XYZ add color3");
viewer->setPointCloudRenderingProperties(pcl::visualization::PCL_VISUALIZER_POINT_SIZE,3,"XYZ add color3");
viewer->addCoordinateSystem(1.0);
return (viewer);
}
/**
* @brief 保存为图片
*/
void Range_Image_write(const pcl::RangeImage::Ptr& rangeimage_ptr){
float *ranges = rangeimage_ptr->getRangesArray();
unsigned char* rgb_image = pcl::visualization::FloatImageUtils::getVisualImage(ranges,rangeimage_ptr->width,rangeimage_ptr->height);
pcl::io::saveRgbPNGFile("/home/n1/notes/pcl/extra_broder/saveRangeImageRGB.png",rgb_image,rangeimage_ptr->width,rangeimage_ptr->height);
}
// class MyBEXT:pcl::RangeImageBorderExtractor{
// public:
// void setParams(){
// }
// }
int main(int argc, const char** argv) {
PointCloud<PointXYZ>::Ptr cloud(new PointCloud<PointXYZ>());
pcl::PointCloud<pcl::PointWithViewpoint> far_ranges;
//读取点云
io::loadPCDFile("/home/n1/notes/pcl/extra_broder/test.pcd",*cloud);
io::loadPCDFile("/home/n1/notes/pcl/extra_broder/test.pcd",far_ranges);
// //io::loadPLYFile("/home/n1/notes/pcl/extra_broder/init.ply",*cloud);
// //转换为深度图
StatisticalOutlierRemoval<PointXYZ> SOR;// 初始化对像离群点滤波
SOR.setInputCloud(cloud);
SOR.setMeanK(50); ///最临近距离求取均值点的个数
SOR.setStddevMulThresh(1); //设置阈值 阈值=均值+设置系数*标准差 小于阈值为内点,大于阈值为离群点
SOR.filter(*cloud);
pcl::RangeImage::CoordinateFrame coord_frame=pcl::RangeImage::CAMERA_FRAME;//X向右,y向下,z向前
float angulareslution=(float)(0.5f*(M_PI/180.0f)); //1度
float noiseLevel=0.0;
float minRangle=0.0; //通过归一化的Z缓冲器创建图像,minRangle>0,可视化最小距离
int borderSize=1; /*border_size获得深度图像的边缘的宽度:在裁剪图像时,如果 borderSize>O ,将在图像周围留下当前视点不可见点的边界*/
pcl::RangeImage::CoordinateFrame coordinate_frame = pcl::RangeImage::CAMERA_FRAME;
pcl::RangeImage::Ptr rangeimage_ptr(new pcl::RangeImage());
Eigen::Affine3f sensor_pose= (Eigen::Affine3f)Eigen::Translation3f(0.0f, 0.0f, 0.0f);
rangeimage_ptr->createFromPointCloud(*cloud,angulareslution,pcl::deg2rad(360.0f),pcl::deg2rad(180.0f),sensor_pose,coordinate_frame,noiseLevel,minRangle,borderSize);
rangeimage_ptr->integrateFarRanges(far_ranges); //很重要
//保存为图片
Range_Image_write(rangeimage_ptr);
//提取边界 提取物体边界、阴影边界、毗连与被遮挡背景的点集
pcl::RangeImageBorderExtractor BEXT; //边缘提取容器
pcl::RangeImage& range_image = *rangeimage_ptr;
BEXT.setRangeImage(&range_image);
pcl::PointCloud<pcl::BorderDescription> border_descriptions;//边界点的描述信息
// BorderDescription:
// x,y,bitset(32)
BEXT.compute(border_descriptions);
pcl::PointCloud<pcl::PointWithRange>::Ptr obscaleborder_ptr(new pcl::PointCloud<pcl::PointWithRange>());
pcl::PointCloud<pcl::PointWithRange>::Ptr viaborder_ptr(new pcl::PointCloud<pcl::PointWithRange>());
pcl::PointCloud<pcl::PointWithRange>::Ptr shadownborder_ptr(new pcl::PointCloud<pcl::PointWithRange>());
for(int i=0;i<rangeimage_ptr->height;i++){
for(int j=0;j<rangeimage_ptr->width;j++){
//当为物体边界
if(border_descriptions.points[i*range_image.width + j].traits[pcl::BORDER_TRAIT__OBSTACLE_BORDER]){
obscaleborder_ptr->points.push_back(range_image.points[i*range_image.width + j]);
}
//via
if(border_descriptions.points[i*range_image.width + j].traits[pcl::BORDER_TRAIT__VEIL_POINT]){
viaborder_ptr->points.push_back(range_image.points[i*range_image.width + j]);
}
//隐藏点
if(border_descriptions.points[i*range_image.width + j].traits[pcl::BORDER_TRAIT__SHADOW_BORDER]){
shadownborder_ptr->points.push_back(range_image.points[i*range_image.width + j]);
}
}
}
//可视化
cout<<"obscaleborder_ptr size:"<<obscaleborder_ptr->size()<<endl;
cout<<"viaborder_ptr size:"<<viaborder_ptr->size()<<endl;
cout<<"shadownborder_ptr size:"<<shadownborder_ptr->size()<<endl;
boost::shared_ptr<pcl::visualization::PCLVisualizer> viewer (new pcl::visualization::PCLVisualizer ("3D Viewer"));
viewer=RGB_viwer(cloud,obscaleborder_ptr,viaborder_ptr,shadownborder_ptr);
while (!viewer->wasStopped()){
viewer->spinOnce (100);
boost::this_thread::sleep (boost::posix_time::microseconds (100000));
}
return 0;
}
- 修改参数(不建议使用)
自定义一个类:
class MyBEXT:public pcl::RangeImageBorderExtractor{
public:
void set_params(int max_no_of_threads=2,int pixel_radius_borders=3,int pixel_radius_plane_extraction=2,
int pixel_radius_border_direction=3,float minimum_border_probability=0.8f,int pixel_radius_principal_curvature=2){
parameters_.max_no_of_threads=max_no_of_threads;
parameters_.pixel_radius_borders=pixel_radius_borders;
parameters_.pixel_radius_plane_extraction=pixel_radius_plane_extraction;
parameters_.pixel_radius_border_direction=pixel_radius_border_direction;
parameters_.minimum_border_probability=minimum_border_probability;
parameters_.pixel_radius_principal_curvature=pixel_radius_principal_curvature;
// int max_no_of_threads=1; 线程数
// int pixel_radius_borders=3; 边阶搜索半径
// int pixel_radius_plane_extraction=2; 计算平面变化棒经
// int pixel_radius_border_direction=3; 点主要防线的半径
// float minimum_border_probability=0.8f; score评分超过该值认为是边界点
// int pixel_radius_principal_curvature=2; 计算兴趣点主曲率的半径
}
};
替换:
// pcl::RangeImageBorderExtractor BEXT; //边缘提取容器
// pcl::RangeImage& range_image = *rangeimage_ptr;
// BEXT.setRangeImage(&range_image);
// pcl::PointCloud<pcl::BorderDescription> border_descriptions;//边界点的描述信息
// // BorderDescription:
// // x,y,bitset(32)
// BEXT.compute(border_descriptions);
MyBEXT BEXT; //边缘提取容器
pcl::RangeImage& range_image = *rangeimage_ptr;
BEXT.setRangeImage(&range_image);
BEXT.set_params(2,3,2,3,0.7,2);
pcl::PointCloud<pcl::BorderDescription> border_descriptions;//边界点的描述信息
BEXT.compute(border_descriptions);