摘要：

知识蒸馏已成为提高小型神经网络性能的标准方法。目前知识蒸馏主流的方法是：对网络的输出层进行蒸馏和对网络的中间特征层进行蒸馏。一些文献表明：蒸馏网络的中间层更能提高学生网络的性能。以往的大部分研究都提出在一个对一个的空间匹配方式下，将教师网络的表示特征转移到学生网络中。然而，人们往往忽视了一个事实，即由于架构差异，同一空间位置上的语义信息通常会有所不同。这极大地削弱了一个对一个蒸馏方法的基本假设。因此，RMIT大学和阿里巴巴团队提出了一种新颖的一对多空间匹配的知识蒸馏方法。具体来说就是通过教师网络中间层特征图的每个像素点与学生网络特征图的每个像素点的相似度的计算，对学生网络特征图的每一个像素间进行加权计算，这种相似性是由一个面向目标的Transformer生成的，即蒸馏损失是所有学生组成部份的加权总和。这种方法在各种计算机视觉基准上（例如ImageNet、Pascal VOC和COCOStuff10k）明显超越了现有方法。

论文连接： https://arxiv.org/pdf/2205.10793.pdf
论文代码： https://github.com/sihaoevery/TaT

一、动机

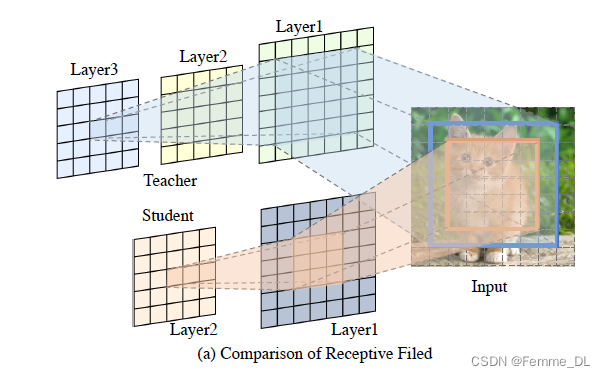
主要动机是对神经网络中间层进行知识蒸馏时，对于同一位置上的教师接受域和学生接受域的点学到的感受野的大小不同，教师网络的网络层数更多，因此，接受域学习到的语义信息更加丰富。如图（a)所示：教师网络的layer3特征图的中间接受域和学生网络layer2特征图的中间接受域对应的input图像中的感受野的大小却是不相同的。

如果此时，将教师网络和学生网络中的这两个特征图进行一一匹配知识蒸馏的话，就会导致学生特征图和教师特征图学习到的语义信息存在差异，此时得到的就是次优解。

二、TaT Knowledge Distillation 介绍

符号假设：
$T$ 和 $S$ 分别表示教师网络和学生网络，都为卷积神经网络
$F^T\in {\mathbb{R}}^{H\times W\times C}$: 教师特征图
$F^S\in {\mathbb{R}}^{H\times W\times C^{{}^{\prime }}}$: 学生特征图
其中，$H$,$W$ 表示特征图的高和宽，$C$ 表示通道数。
$\Gamma (\cdot )$ : 将特征张量从3维转换成2维的函数
$f_i^t,f_i^s$ : 分别表示教师网络和学生网络在同一空间位置的第 $i$ 个特征图

1. 对神经网络的输出层进行知识蒸馏

神经网络的输出层的神经元，往往表示的是输入为某个类别的概率值，因此对于input $x$，对应的教师网络的输出经过softmax函数后得到类别的概率输出为$\sigma (T(x))$，学生网络的输出为$\sigma (S(x))$，计算这两个输出之间的损失，就是计算这两个向量之间的距离，使用KL散度公式：
$${\mathcal{L}}_{\mathrm{KL}}=\mathrm{KLD}\left(\sigma \left(\frac{T(x)}{\tau }\right),\sigma \left(\frac{S(x)}{\tau }\right)\right)$$，其中 $\tau$ 是蒸馏温度。

2. 对神经网络的中间层进行知识蒸馏

在不失一般性的情况下，假设 $C$ 和 $C^{{}^{\prime }}$ 的大小相同，将所有通道的教师特征图和学生特征图reshape为2D矩阵，矩阵中的每一行都是一个特征图通过$N=H\times W$ 得到的：
$$\begin{array}{rl}{f}^s& =\Gamma \left(F^S\right)\in {\mathbb{R}}^{N\times C},\\ f^t& =\Gamma \left(F^T\right)\in {\mathbb{R}}^{N\times C}.\end{array}$$
变形：
$$\begin{array}{rl}{f}^{s\top }& =\left[f_1^s,f_2^s,f_3^s,\dots ,f_N^s\right]\\ f^{t^{\top }}& =\left[f_1^t,f_2^t,f_3^t,\dots ,f_N^t\right].\end{array}$$
通过空间位置上，一对一特征匹配（FM）的方式计算特征图之间的损失：
$${\mathcal{L}}_{\mathrm{FM}}={\Vert F^S-F^T\Vert }_2=\sum _{i=1}^N{\Vert f_i^s-f_i^t\Vert }_2$$

3. TaT方法的介绍

3.1 非参数版本的 TaT 算法

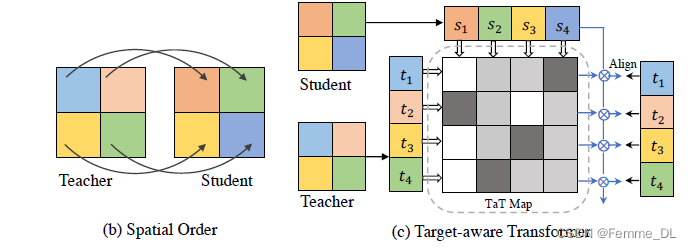
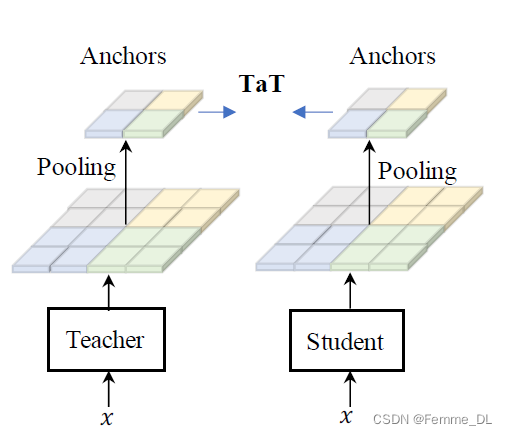
TaT 提出了一种一对多的空间匹配知识蒸馏，允许教师的每个特征位置以动态方式教导整个学生特征。为了使整个学生模拟教师的空间组成部分，TaT 提出了Target-aware Transformer（TaT），以教师网络智能地重新配置学生特征在特定位置的语义。给定教师的空间组成部分（对齐目标），使用TaT指导整个学生在相应位置重构特征。在对齐目标的条件下，TaT应该反映出与学生特征的组成部分的语义相似性。我们使用线性操作符来避免改变学生语义的分布。转换操作符 $W^i$ 的表述可以定义为：
$$\begin{array}{rl}{W}^i& =\sigma \left(⟨f_1^s,f_i^t⟩,⟨f_2^s,f_i^t⟩,\dots ,⟨f_N^s,f_i^t⟩\right)\\ & =\left[w_1^i,w_2^i,\dots ,w_N^i\right]\end{array}$$
其中，$<\cdot ,\cdot >$ 表示内积，$\Vert W^i\Vert =1$，$\sigma$ 对内积进行归一化。每一个 $W^i$ 类似于门，控制着教师网络中的2维矩阵的每个像素点传播到第i个重新配置的学生特征像素点的语义量。然后，每个学生网络的特征信息点乘以相对应的语义权重，得到的学生特征图与原来的教师网络在这个空间位置的特征图做损失，就是图中表示的Align。

公式表示如下：
$$f_i^{s^{\prime }}=w_1^i\times f_1^s+w_2^i\times f_2^s+\cdots +w_N^i\times f_N^s$$
然后得到的乘过语义权重的学生特征矩阵$f_i^{s^{{}^{\prime }}}$ 与 教师网络的特征矩阵 $f_i^t$ 计算损失差异得到了TaT损失函数：
$${\mathcal{L}}_{\mathrm{TaT}}={\Vert f^{s^{\prime }}-f^t\Vert }_2$$

3.2 参数版本的TaT 算法

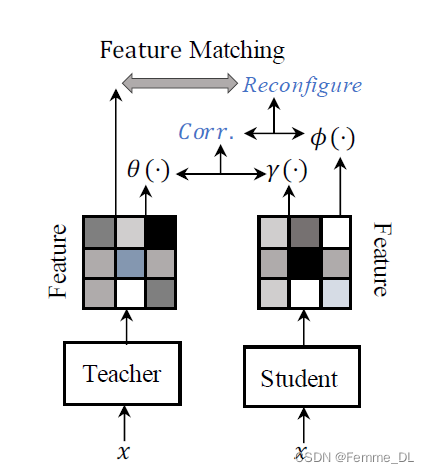
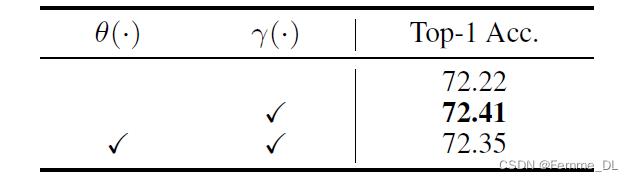
首先需要说明的是，作者在实验中发现参数版本的TaT算法比非参数版本的TaT算法的效果要好，这是因为，非参数方法仅依赖于原始特征，在引入了带有额外线性转换的参数化方法应用于学生特征和教师特征。观察到，在消融研究中，参数化版本表现比非参数化版本更好。因此，学生网络中经过计算权重特征的公式如下：
$$f^{s^{\prime }}=\sigma \left(\gamma \left(f^s\right)\cdot \theta {\left(f^t\right)}^{\top }\right)\cdot \varphi \left(f^s\right),$$
其中，$\theta (\cdot )$, $\gamma (\cdot )$ 是$3\times 3$的卷积加批归一化操作组成的线性方程。

3.3 TaT算法的损失函数

算法的损失函数由硬损失、软损失和TaT损失三部分组成，公式如下：
$$\mathcal{L}=\alpha {\mathcal{L}}_{\text{Task }}+\beta {\mathcal{L}}_{\mathrm{KL}}+ϵ{\mathcal{L}}_{\mathrm{TaT}}$$
其中, $\alpha$,$\beta$,$\gamma$ 表示这三种损失的权重系数。

3.4 分层蒸馏

虽然TaT的方法克服了以往一对一空间匹配方式的限制，但是想象一下，教师网络中的每一个二位特征图的像素点都要和学生网络的特征像素点做内积，这样就会有很大的计算量。当处理大型特征图时，TaT映射的计算复杂性将变得难以处理。假设特征图的空间维度为 $H$ 和 $W$，这意味着计算复杂度将达到 $O(H^2\cdot W^2)$。因此，论文中提出了一种分层蒸馏的方法来解决这种大型特征图的限制。该方法包括两个步骤：1）补丁组蒸馏，将整个特征图分割成较小的 patch，从而从教师到学生蒸馏局部信息；2）进一步将局部补丁总结为一个向量，并对全局信息进行蒸馏。

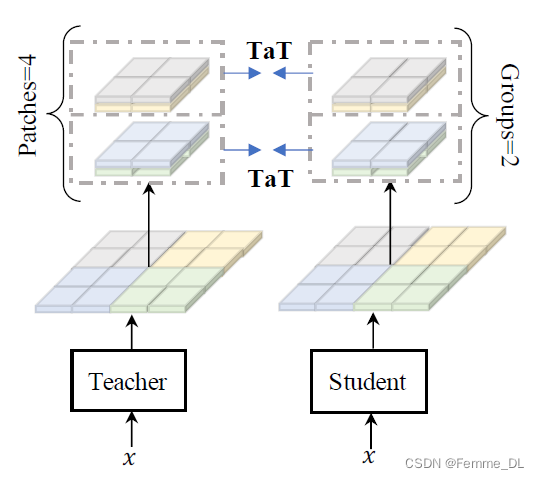
3.4.1 Patch-group distillation

在上述提到的情况下，随着输入特征图的空间维度增加，知识蒸馏变得更加困难。一种直接的解决方案是将特征图分割成小块，并在各个小块内进行独立的知识蒸馏。然而，这种方法完全忽略了小块之间的相关性，导致了次优的解决方案。这种方法允许学生从小块中学习局部特征，并在一定程度上保留它们之间的相关性。给定原始的学生特征$F^S$和教师特征$F^T$，它们被分割成大小为 $h\times w$ 的 $n\times m$ 个小块，其中 $h=H/n$，$w=W/m$。它们被进一步按顺序排列成 $g$ 个组，每个组包含 $p=n\cdot m/g$ 个小块。具体而言，组内的小块将以通道方式进行拼接，形成一个新的大小为 $h\times w\times c\cdot g$ 的张量，后续将用于蒸馏。这样，新张量的每个像素包含来自原始特征的 $p$ 个位置的特征，明确包含了空间模式。因此，在蒸馏过程中，学生不仅可以学习单个像素，还可以学习它们之间的相关性。直观来说，较大的组会引入更丰富的相关性，但复杂的相关性会变得更难学习。我们在实验中研究了不同组大小的有效性。
小块组蒸馏可以简单地通过用重新组织后的输入取代原始输入来表示，这个变体被标记为$L_{TaT}^p$。为了放宽对小块组中空间模式的严格限制，在我们的实验中将 $\theta (\cdot )$ 设定为线性变换。

3.4.2 Anchor-point distillation

Patch-group distillation 方法可以学习到细粒度特征，保留了一定程度上的 patch 之间的空间相关性，但无法感知远距离的依赖关系。对于复杂场景，长距离依赖是捕捉不同对象之间关系（例如布局）的重要因素。作者提出了 anchor-point distillation 方法来解决这一困境。该方法通过将局部区域总结为紧凑的表示，称为锚点，以代表描述给定区域语义的局部区域，形成新的较小尺寸的特征图。由于新特征图包含原始特征的摘要，因此可以近似替代原始特征图以获取全局依赖关系。作者使用平均池化提取锚点，然后将所有锚点分散到关联位置，形成新的特征图。锚点特征用于蒸馏（distillation），并且通过 $L_{TaT}^A$ 目标进行表示。patch-group distillation 方法使得学生模仿局部特征，而 anchor-point distillation 方法允许学生在粗糙的锚点特征上学习全局表示，两者相辅相成。因此，将这两个目标组合起来可以发挥两种方法的最佳效果。

三、实验结果

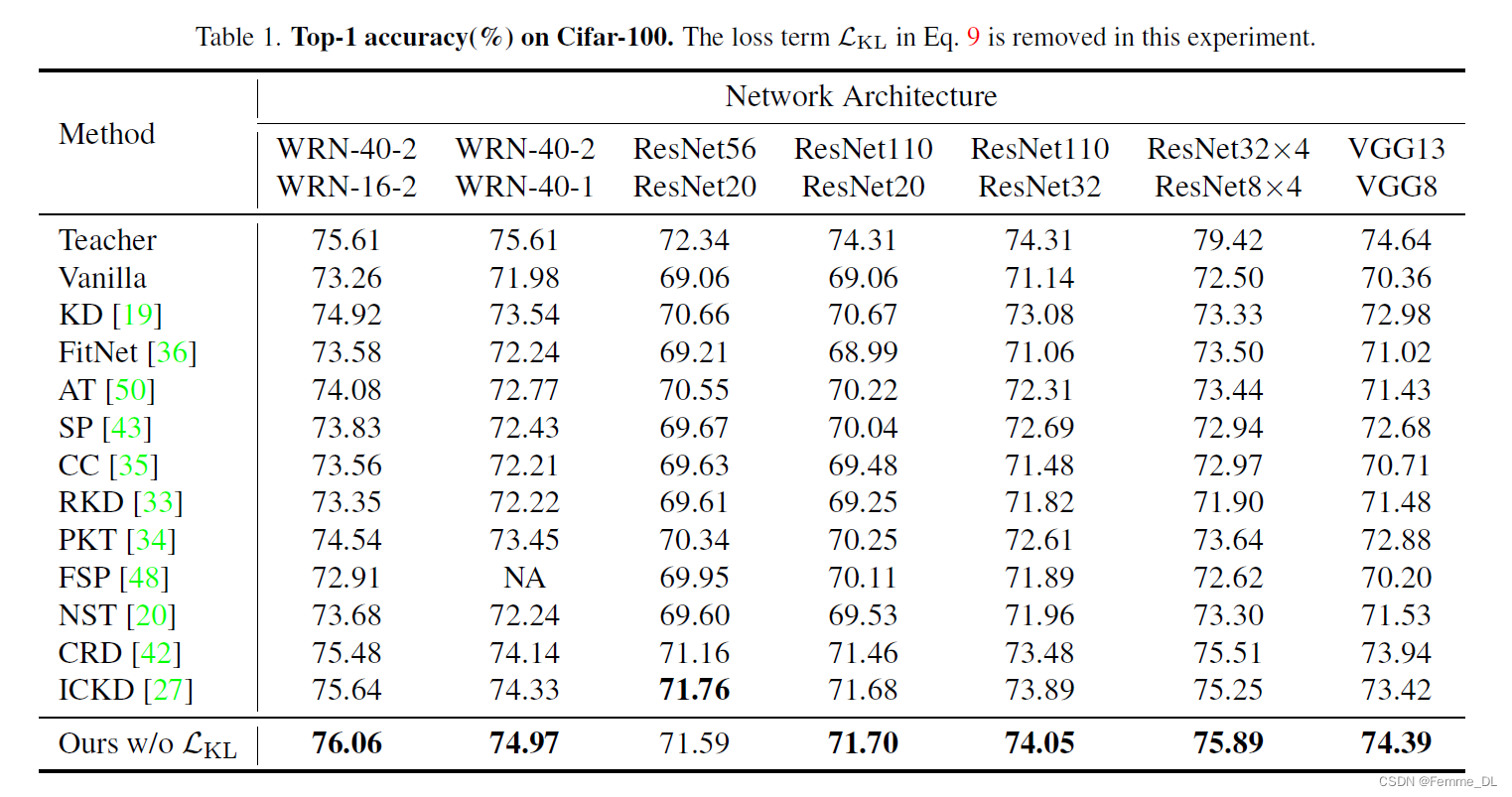
1. 图像分类实验

• 下图是非参数TaT算法在分类任务上的表现（Cifar100）：
  
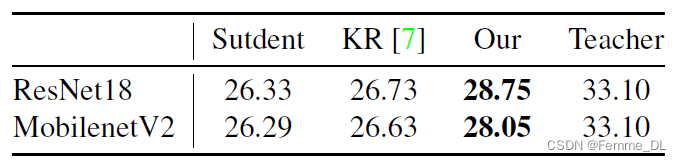
• 参数化TaT算法在分类任务上的表现（ImageNet）：
  

2. 图像分割实验

四、结论

这项工作发展了一个知识蒸馏的框架，通过一种Target-aware Transformer，使得学生模型能够汇聚有用的语义信息，以增强每个像素的表达能力，从而使学生模型能够整体行动来模仿教师模型，而不是并行地最小化每个空间位置上的特征差异。该方法成功地扩展到语义分割，通过提出的分层蒸馏方法，包括补丁组和锚点蒸馏，旨在关注局部特征和长距离依赖关系。经过彻底的实验证明了该方法的有效性，并推动了最新技术的发展。