前言

对于成功的数据预处理而言，把握数据的全貌是至关重要的，基本统计描述可以用来识别数据的性质，凸显哪些数据值应该视为噪声或者是离群点。这一节我们将要讨论三类数据的基本统计描述，包括数据的中心趋势的度量，数据的离散趋势度量以及基本的统计作图。

一、数据的中心趋势度量

直观的来说是给定数据中的一个属性，那么这个属性的值大部分落在何处呢？具体的我们接下来会讨论。代表中心属性的几个指标包括均值，中位数，众数和中列数。考察度量数据中心趋势有很多方法，在这里我们主要介绍均值，中位数和众数，我们先看一个数据，这个数据如下表：

某个属性$X$对应着工资水平，它记录了$x_1,x_2,\dots ,x_N$为属性$X$的$N$个观测值。我们想知道大部分值是落在哪里？这也是反映了数据的中心趋势的思想。刚才我们说了中心趋势，它的度量包括均值，中位数，众数中列数。那么数据集的中心呢是最常用，最有效的这种度量方法就是均值。所以呢咱们首先从均值讲起，

1、平均值

$$\mathrm{x}\text{ 的平均值 }=\bar{x}=\frac{{\sum }_{i=1}^N{x}_i}{N}$$
假设工资水平是如下的值，我们把这个工资水平按照递增顺序排列。那么我们用上面的均值的计算公式能够得到这个工资水平的平均值为58000美元。
$$30,31,47,50,52,52,56,60,63,70,70,110$$
则均值为：$$(30+31+47+50+52+52+56+60+63+70+70+110)/12=58$$

2、加权平均值

有的时候属性x的每一个观测值它的权重是不一样的。权重呢反映出他们所依附的对应值的意义，重要性或者出现的频率。在这种情况下呢，我们可以计算加权平均值，加权平均值的计算公式如下：
$$\text{ 加权平均值 }=\frac{{\sum }_{i=1}^N{x}_i\cdot w_i}{{\sum }_{i=1}^N{w}_i}$$
其中，$w_i$是每个数据值的权重。加权算术平均的计算方法在对于不同数值它有不同的权重来说是非常有用的。

3、截尾均值

尽管均值是描述数据集当中最有用的一个指标。但是他并非总是最佳的方法，有的时候这个均值对有一些极端值的影响非常敏感，比如说公司的平均薪水可能会被少数几个高收入的经理显著的推高了，或者一个班的考试平均成绩可能会被少数的几个很低的成绩给拉低了。为了抵消这种少数极端值的影响，我们可以用截尾均值。截尾均值有时也被翻译成修剪的平均数，结尾均值就是丢弃极端之后的均值，比如说我们对上面的工资观测值进行排序并且计算均值之前去掉最高的和最低的2%不要在两端截取太多，比如说有的同学截取20%因为这可能会导致丢失很有价值的信息。

4、中位数

对于倾斜的或者非对称的数据来说，数据中心更好度量的是中位数。中位数是有序数据值的中间值，它是把数据较高的一半和较低的一半分开的这个值。在概率和统计学当中，中位数一般是对于数值数据，然而我们把这一概念推广到序数数据。假设给定某属性$X$的$N$个值按照递增顺序排列：

• 如果$N$是奇数，则中位数则是该有序级的中间值
• 如果$N$是偶数，则中位数不唯一，它是最中间的两个值和他们之间的任意值，在x是数值属性的情况下根据约定中位数取作最中间两个值的平均值。

我们一起来看个例子吧仍然是上面这个工资水平的数据集，大家找一找它的中位数是多少？我们先把这个数据按照递增顺序排序，
$$30,31,47,50,52,52,56,60,63,70,70,110$$
发现有偶数个观测值一共12个，因此中位数不唯一，它可以是最中间两个值，52和56中间的任意一个值。根据咱们的约定，我们指定了这两个最中间的值的平均值为中位数也就是52和56的均值54，所以工资收入的中位数是54000美元。假设我们只有该表当中的前11个值，$$30,31,47,50,52,52,56,60,63,70,70$$
也就是奇数的观测值，那么这个中位数就是第6个数据值52.

5、众数

数据集的众数是集合当中出现最频繁的值，因此可以对定性和定量属性确定众数，可能最高频率对应多个不同的值，导致多个众数具有一个，两个，三个众数的数据结合，分别对应于单峰的，双峰的和三峰的。一般的来说：

• 有两个或者更多的众数的数据集是多峰的；
• 在另一种极端的情况下，如果每个数据值仅出现了一次，那么他没有众数。

还是看这个工资收入水平的例子吧，
$$30,31,47,50,52,52,56,60,63,70,70,110$$
有两个众数，52000美元和7万美元对于适度倾斜非对称的单峰数据，我们有下面的经验关系
平均数-众数约等于三倍的平均数减中位数
这意味着如果均值和中位数已知，则适度倾斜的单峰频率曲线的众数容易近似的计算。

中列数

中列数也可以用来评估数值数据的中心趋势，中列数是数据集的最大和最小值的平均值，我们看这个例子。
$$30,31,47,50,52,52,56,60,63,70,70,110$$
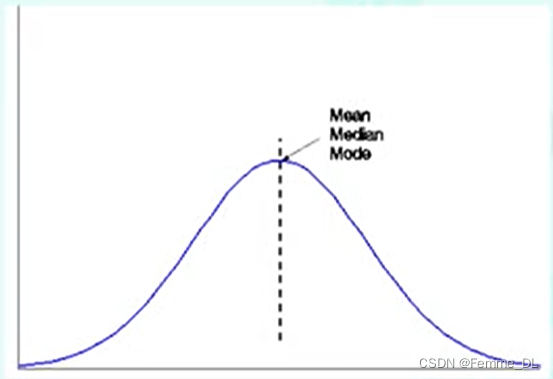
最小值为3万，最大值为11万，所以我们的中列数为两个的平均值7万。在具有完全对称的数据分布的单峰频率曲线当中，均值、中位数和众数都具有相同的中心值这个可以从下图当中看出来。

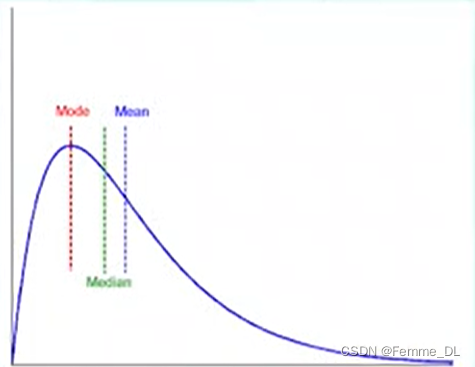
在大部分实践应用中数据都是不对称的，他们可能是正倾斜的，其中众数出现在小于中位数的值上。

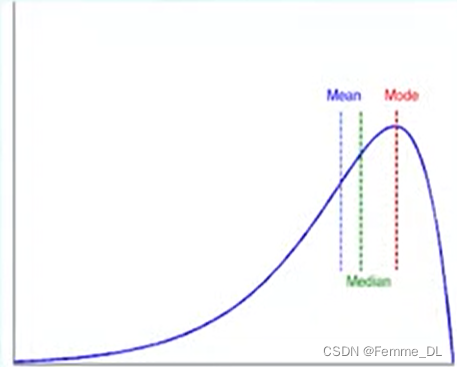
或者是负倾斜的，其中众数出现在大于中位数的值上。

二、数据的离散趋势

数据的离散程度，也就是数据的离散分布。最常见的有分位数，极差，分位数极差，五数概括以及盒图，盒图呢也称为箱线图，以及标准差和变异系数，对于识别离群点这些度量都是十分有用的。

1、极差

极差也叫全距，是整个距离的意思，设$x_1,x_2,\dots ,x_N$是某数值属性$X$的观测值，该数据集的极差是最大值与最小值之差我们记为公式 $$\mathrm{Range}(X)=\mathrm{Max}(X)-\mathrm{Min}(X)$$

• 极差是数据中最大与最小间的差距，
• 是衡量数据变异程度最简单的描述，
• 对最大与最小数的值敏感性很强。

2、分位数

中位数是分位数的一个特例。
假设属性$X$的数据以数值递增的顺序排列，我们可以挑选某些数据点把数据分布化成大小相等的连贯集，这些数据的点我们称之为分位数，分位数也被称为分位数点，是指一个随机变量的概率分布范围分为几个等份的数值点，常用的有

• 中位数
• 4分位数，
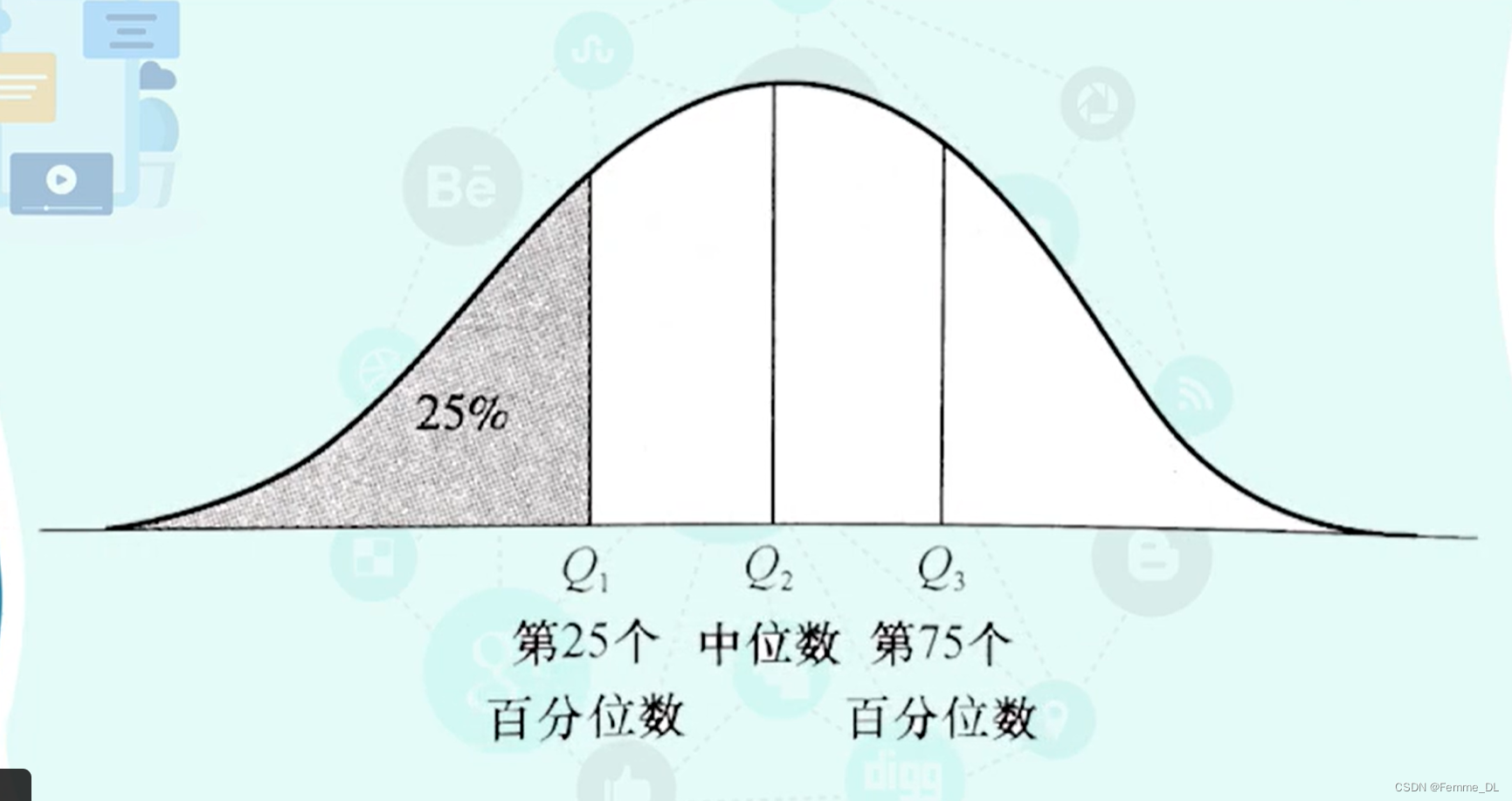
• 百分位数，
  

在这里第 $p$ 个百分位数就是指至少有 $p$ 的数据小于或等于这个值而且至少有$(100-p)\%$ 的数据项大于或等于这个值。

计算方法是

• 先递增排序，
• 然后计算位置的指数，$i=p/100\times n$
• 如果$i$不是整数，则向上取整如果$i$是整数，则$p$分位数为第2项和第2+1项的数据的平均值。
  例子：
  
  以上70个数据，计算$90\%$分位数：

• 则位置的指数：$\mathrm{i}=(\mathrm{p}/100)\mathrm{n}=(90/100)70=63$
  63是整数，所以$90\%$分位数是63位和64位数的平均数：
• \text { 90th Percentile }=(580+590) / 2=585

3、四分位数

四分位数是特定的百分位数，

• 第一个四分位数为$25\%$百位数；
• 第二个四分位数为$50\%$百分位数，也就是中位数;
• 第三个四分位数为$75\%$百分位数。
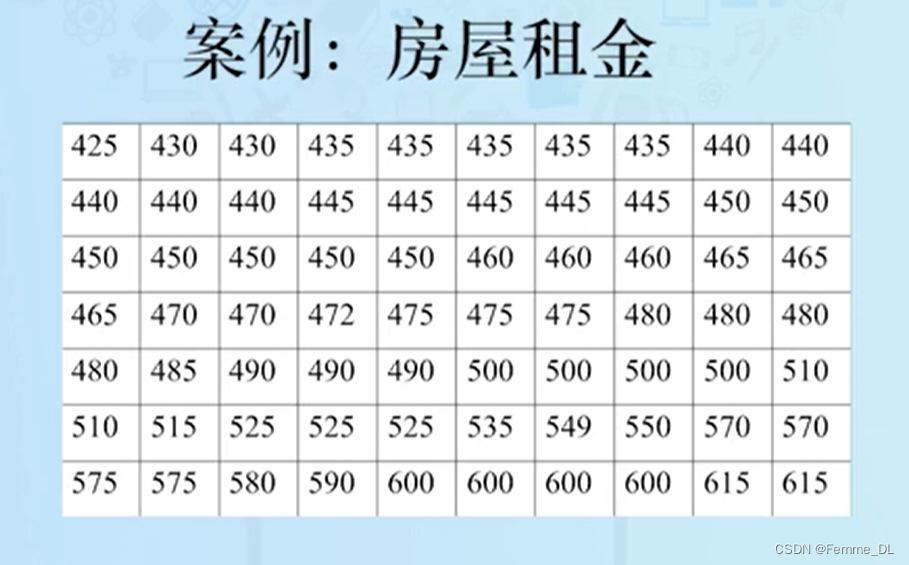
  仍以上图中的房屋租金的数据为例，计算一下第三个四分位数也就是$75\%$百分位数：

1. 将数字从小到大排序，计算位置指数：$$\mathrm{i}=(\mathrm{p}/100)\mathrm{n}=(75/100)70=52.5\approx 53$$（向上取整）
2. 租金的第53位是525，所以房屋租金的第三个四分位数是525.

4、四分位极差

定义： 第1个和第3个四分位数之间的距离。
公式：$\mathrm{IQR}=\mathrm{Q}3-\mathrm{Q}1$
特点： 该距离是散布的一种简单度量，能够克服极端值的影响;
仍以房屋租金为例：
Interquartile Range 四分位极差, 又称四分位点内距

• Interquartile Range $=$ Q3 - Q1 $=525-445=80$
• 3rd Quartile $(\mathrm{Q}3)=525$ 1st Quartile $(\mathrm{Q}1)=445$

5、分布的五数概括

最能反映数据重要特征的五个数是中位数、四分位数、最小和最大观测值组成这五个数，也称为分布的五数概括。按照次序依次是minimum ，$Q1$，median, $Q3$， maximum，把他们写出来就是五数概括。识别可疑的离群点有一个通用的规则，这个规则是如果数值落在第三个四分位数之上或第一个四分位数之下至少$1.5\times IQR$处的值可以被看作是可疑的离群点。

6、箱线图

和五数概括有关的就是箱线图，箱线图也称之为盒图——box plot。盒图体现了五数概括有以下几个特征，

• 在盒图当中，第一个四分位数和第三个四分位数分别确定了盒子的底部和顶部；
• 盒子中间的粗线就是中位数所在的位置；
• 由盒子向上向下伸出的垂直部分称之为触须，表示数据数据的散布范围，通常最原点是$1.5\times IQR$。

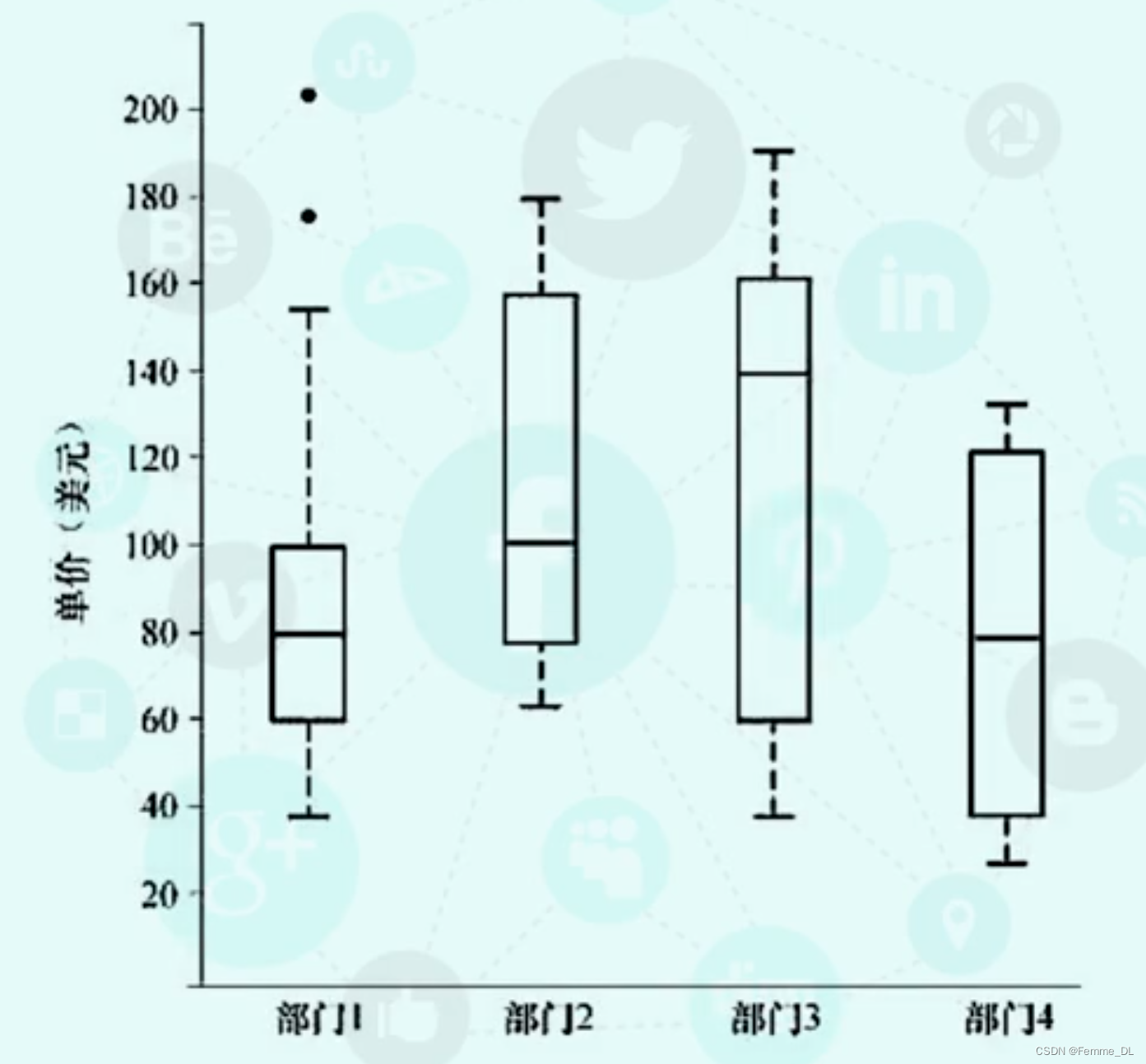
让我们来看一个盒图： 这个盒图是给定的时间段，四个部门销售的商品单价数据的盒图。

说明：对于部门一，我们看到销售商品单价的中位数是80美元，$Q1$是60美元，$Q3$ 是100美元，IQR的值是40， 1.5倍的IQR值是60。值得注意的是该部门的两个边缘的观测值，它们被个别的绘出来，因为他们的值175和202都超过了第三个四分位数的1.5倍的IQR。

方差和标准差

方差variance和标准差standard deviation都是数据离散度量的指标，方差是各个数据值与平均值之间的差异如果方差或者标准差比较小，则表示数据观测值趋向于均值如果标准差或者是方差比较大，那么表示数据分布在一个较大的值域中。我们令数值属性$X$ 的$N$ 个观测值 $x_1,x_2,\dots ,x_N$，记方差是：
$${\sigma }^2=\frac{\sum {\left(x_i-\mu \right)}^2}{N}$$
观测值的标准差是方差的平方根：
$$\sigma =\sqrt{{\sigma }^2}$$
注意 样本方差和总体方差有所不同，下面我们一起来看个例子, 以工资收入水平为例计算:
$$30,31,47,50,52,52,56,60,63,70,70,110$$

• 均值：58
• 令$N=12$，根据方差公式计算方差为：379.17
• 标准差：19.14
  作为发散性的度量，标准差的性质有如下，

1. 当选择均值作为中心度量时，可以选择标准差度量数据的发展程度；
2. 仅当不存在发散时，也就是说当所有的观测值都具有相同值的时候，标准差等于零，否则标准差大于零；
3. 一个观测值一般不会远离均值超过标准差的数倍；
4. 变异系数等于标准差和均值的比值，再乘以100。

总结

数据的描述性统计旨在对数据集进行总结和描述，以便更好地理解数据的特征和分布。其中包括集中趋势（central tendency）和离散趋势（dispersion）这两个重要概念。

集中趋势（Central Tendency）：

1. 均值（Mean）： 是数据集中所有数值的总和除以数据点的个数。它是最常用的度量数据集集中趋势的统计量，但受极端值影响较大。

2. 中位数（Median）： 是将数据集中的所有数值按大小排列后位于中间的数值。它对极端值不敏感，能够更好地表示数据的中心位置。

3. 众数（Mode）： 是数据集中出现次数最频繁的数值。有时数据集可能有多个众数。
   。。。

离散趋势（Dispersion）：

1. 范围（Range）： 是数据集中最大值和最小值之间的差异。虽然简单，但受极端值影响较大，不能提供关于数据分布的全面信息。

2. 方差（Variance）和标准差（Standard Deviation）： 方差是每个数据点与均值之差的平方的平均值，标准差是方差的平方根。它们度量数据点与均值的离散程度，标准差更常用且在统计中更具代表性。

3. 四分位数和IQR（Interquartile Range）： 四分位数将数据集分为四个部分，中间的两个分别是中位数的左右两边。IQR表示第三四分位数和第一四分位数之间的距离，提供了关于数据分布紧密程度的信息。
   。。。

这些描述性统计量提供了对数据集中心位置和离散程度的不同角度描述。它们帮助分析人员更好地理解数据的特征，从而做出更准确的推断和决策。选择适当的统计量取决于数据集的特性以及你希望了解的信息。