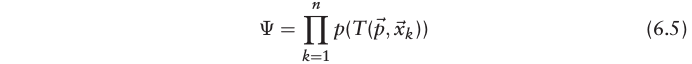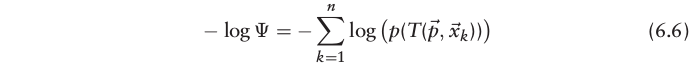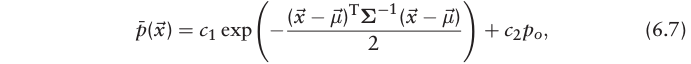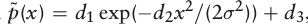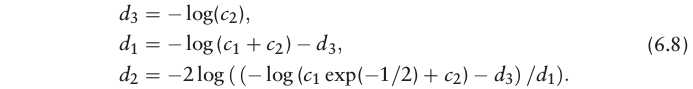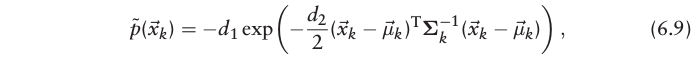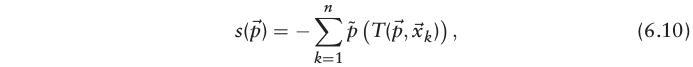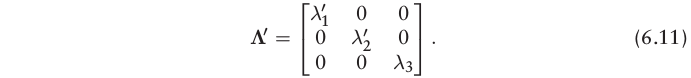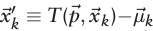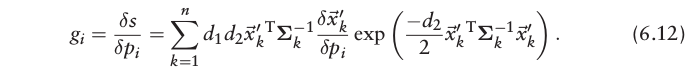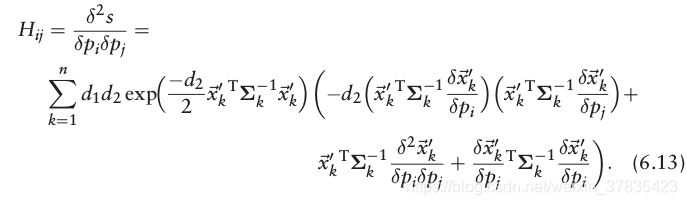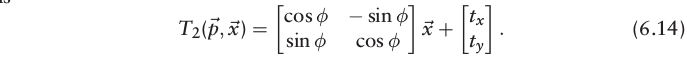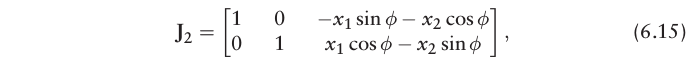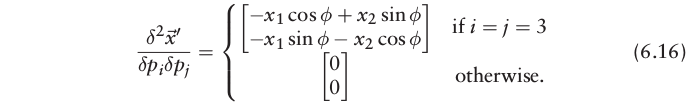前言

NDT算法因其具有较强的鲁棒性而被广泛的应用，下面这些项目中的点云配准算法采用的都是NDT:
Autoware
hdl_graph_slam
hdl_localization
可见该配准方法的重要性，下面我将对这个算法进行分析．

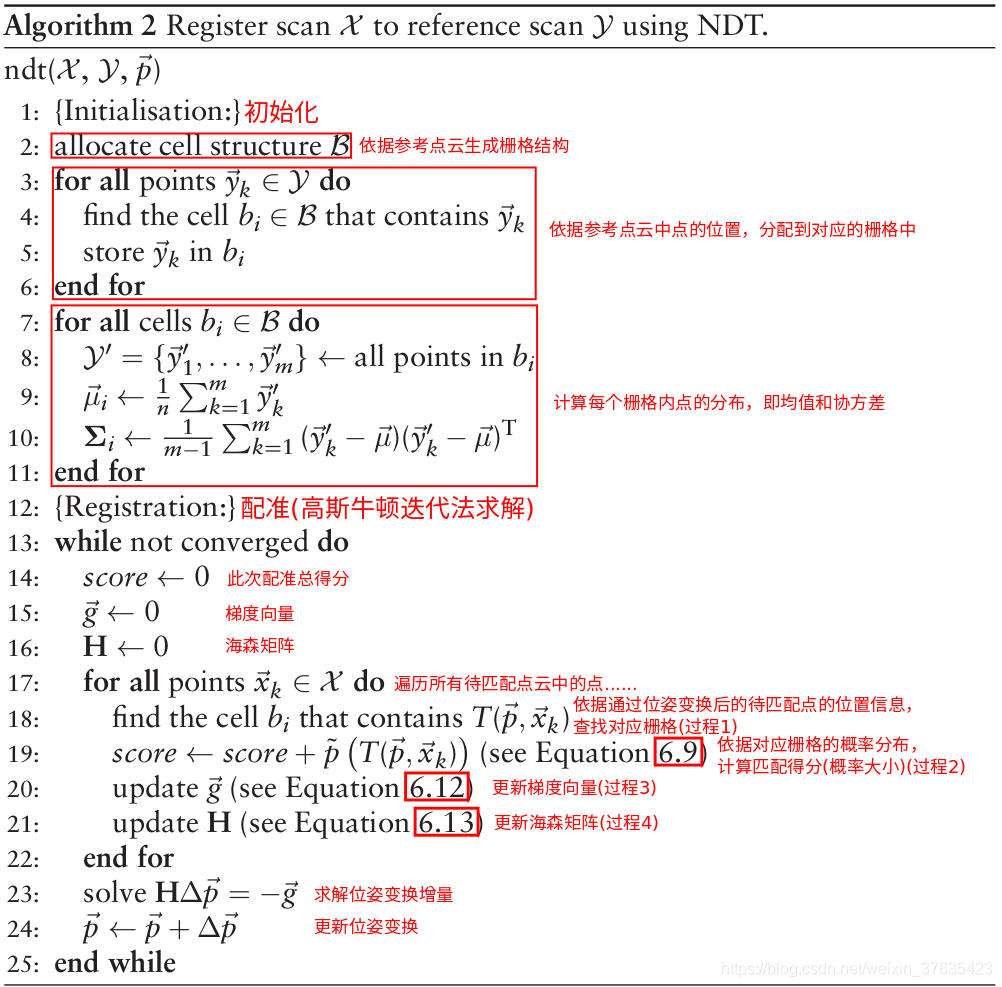
算法流程

依据上述伪码流程可以看出，该算法主要的思路就是将目标点云刻画成多个概率分布，然后通过位姿变换关系将待配准点云转换到目标点云坐标系下，计算转换后待配准点云的总概率，并将此概率的负值作为目标函数，通过高斯牛顿迭代法优化该目标函数以求获得负的最小概率值(即最大概率值)．高斯牛顿迭代公式见第23行，由梯度向量、海森矩阵和待求的位姿增量组成，因此最后整个NDT算法可以简单的归为求解梯度向量、求解海森矩阵和求解位姿增量三个主要过程．下面主要分析较复杂的梯度向量和海森矩阵的求解．

目标函数(对应伪码中的 $score$)

总概率计算如下:

为了能使用高斯牛顿迭代法，需要将目标函数转换成求最小值，而我们的目标是要求取公式(6.5)的最大值，因此可通过下式进行转换，将求取公式(6.5)的最大值转换成求取公式(6.6)的最小值:

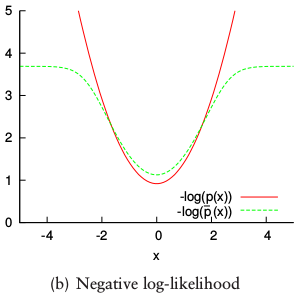
假设每个栅格内点的分布呈正态分布，按公式(6.6)对一个正态分布的PDF求取-log值会出现下图红线所示的没有最大边界问题，该问题会使得噪声对优化结果产生很大影响(如果噪声很大，-log值会非常大，导致优化算法主要的目标是去优化噪声了，结果将会被严重影响)

为了抑制噪声影响，提出了如下正态分布与均匀分布结合的概率分布模型，可以实现图中绿线所示的有边界的效果:

其中常数 $c_1,c_2$ 可以通过要求 $\bar{p}(\vec{x})$ 的概率质量在一个单元格跨越的空间内等于1来确定。公式(6.7)没有简单的一阶、二阶微分．但通过观察上图发现公式(6.7)可以被下式近似:

式中的 $d_1,d_2,d_3$ 可通过令 $x=0,x=\sigma ,x=\infty$建立方程求解，结果为:

该式具有简单的微分方程．基于高斯近似后的概率分布函数如下:

于是最终的目标函数由(6.6)转换成了下式:

注意:
虽然目标函数已确定，但目标函数中的协方差矩阵 $\Sigma$ 的确定需要采取一些策略．因为目标函数中需要求取协方差矩阵的逆 ${\Sigma }^{-1}$ ，如果栅格中的点是共面或共线的，协方差矩阵是奇异的，无法求取逆矩阵，因此由三维空间中三个及以下的点来求取协方差矩阵必然是奇异的．为了解决该问题，NDT算法中的PDF计算要求至少需要5个点，并且当 $\Sigma$ 几乎为奇异值时，就对该协方差进行调整，调整的策略为: 如果 $\Sigma$ 最大的特征值 ${\lambda }_3$ 比 ${\lambda }_1,{\lambda }_2$ 大100倍时，令 ${\lambda }_1={\lambda }_2={\lambda }_3/100$ ，然后再令 $\Sigma =\mathbf{V}{\wedge }^{{}^{\prime }}\mathbf{V}$，其中 $\mathbf{V}$ 包含了 $\Sigma$ 的特征向量，${\wedge }^{{}^{\prime }}$ 的计算如下:

至此确定了NDT算法的目标函数．

梯度向量的求解

令

可得梯度向量:

海森矩阵的求解

示例

从上面的分析可知，NDT算法主要的任务是对梯度向量和海森矩阵的求解，而从公式(6.12)和(6.13)可以看出，针对不同场景，主要的差异体现$\frac{\delta {\vec{\mathbf{x}}}_k^{{}^{\prime }}}{\delta {\mathbf{p}}_i}$和$\frac{{\delta }^2{\vec{\mathbf{x}}}_k^{{}^{\prime }}}{\delta {\mathbf{p}}_i\delta {\mathbf{p}}_j}$．下面以2D场景为例对这两项进行解算．
假设位姿变换参数为$\vec{\mathbf{p}}=(t_x,t_y,\varphi )$，待转换的点为$\vec{\mathbf{x}}=(x_1,x_2)$，则转换位姿变换方程如下:

则$\frac{\delta {\vec{\mathbf{x}}}_k^{{}^{\prime }}}{\delta {\mathbf{p}}_i}$结果为:

$\frac{{\delta }^2{\vec{\mathbf{x}}}_k^{{}^{\prime }}}{\delta {\mathbf{p}}_i\delta {\mathbf{p}}_j}$的结果为:

对于3D场景的示例可查看论文，与二维场景相比，只对三维位姿的求导存在差异．

PCL实现(直接链接PCL库)

2D场景实现
3D场景实现
测试直接看官方demo吧，很简单．

NDT改进版本

ndt_omp

改进1: 引入cpu多线程支持OpenMP
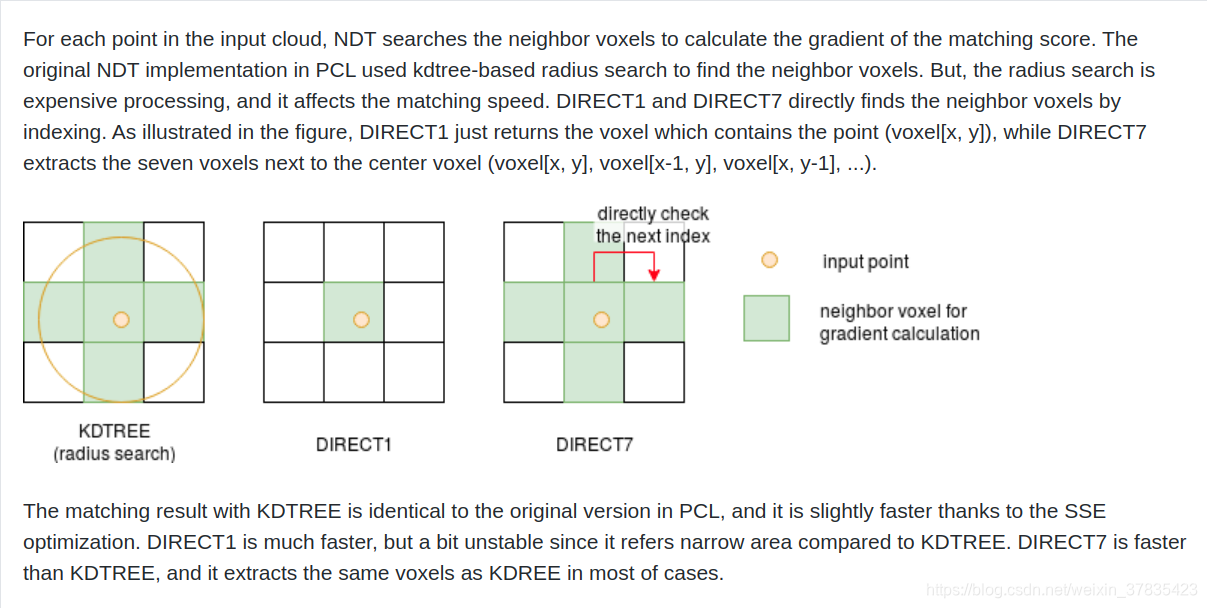
改进2: 搜索速度提升，提升策略如下

参考论文

The Three-Dimensional Normal-Distributions Transform — an Efficient Representation for Registration, Surface Analysis, and Loop Detection