SOSdp 简介 (by zzuzxy)

​

翻译自：
codeforces sos dp
先学知识：状压dp

SOSdp

全称是 $SumoverSubsetsdynamicprogramming$, 意思就是子集和dp，其实在我看来就是状压dp的一种

从一个例题引出$SOSdp$
$$F[mask]=\sum _{i\in mask}A[i]$$
我们说 $i\in mask$即为 $i\&mask=i$, 回忆状压$dp$，这应该很好理解
然后你发现，咦不太对，这个和$FWT$好像，$i\&mask=i和i|mask=mask$是一回儿事
所以破案了，$FWT=SOSdp$
FWT
方法1，$O(4^n)$暴力枚举

for(int mask =0;mask < (1<<N); ++i){
		for(int i = 0;i < (1<<N); ++i)
			if(i&mask == i)
				F[mask] += A[i];
	}   

方法2，$O(3^n)$ 枚举所有子集

for(int mask = 0;mask < (1<<N); ++mask){
		F[mask] = A[0];
		for(int i = mask; i > 0; i = (i-1)&mask)
			F[mask] += A[i];
	} 

方法3，SOS dp $O(n\ast log(n))$

$dp[mask][i]$ 代表$x\&mask=x,x^{\wedge }mask<2^{i+1}$的$A[x]$的和, 意思就是 $dp[mask][i]$是和 $mask$ 只有前$i$个位不同的$A[x]$的和
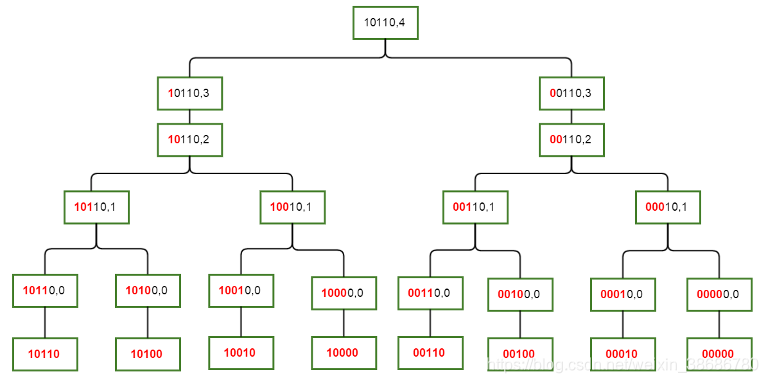
$$dp[mask][i]=\begin{array}{cc}dp[mask][i-1]& mask\&(2^i)=0\\ dp[mask][i-1]+dp[mask\oplus (2^i)][i-1]& mask\&(2^i)=2^i\end{array}$$

如下图

//iterative version
for(int mask = 0; mask < (1<<N); ++mask){
	dp[mask][-1] = A[mask];	//handle base case separately (leaf states)
	for(int i = 0;i < N; ++i){
		if(mask & (1<<i))
			dp[mask][i] = dp[mask][i-1] + dp[mask^(1<<i)][i-1];
		else
			dp[mask][i] = dp[mask][i-1];
	}
	F[mask] = dp[mask][N-1];
}

//memory optimized, super easy to code.
for(int i = 0; i<(1<<N); ++i)
	F[i] = A[i];
for(int i = 0;i < N; ++i) for(int mask = 0; mask < (1<<N); ++mask){
	if(mask & (1<<i))
		F[mask] += F[mask^(1<<i)];
}

扩展及应用

1. CF1208F
   题意：求 $max(a_i|(a_j\&a_k)),1\le i<j<k\le n$
   分析: 从后往前依次将每一个数加入$SOSdp$中，记忆化一下
   参考代码:code

2. SPECIAL PAIRS
   题意： 求$a_i\&a_j=0$的$(i,j)$的个数
   分析：sos dp 即可
   参考代码： code1-FWT code2-sosdp

3. E. Compatible Numbers
   题意： 给定$a_1,..a_n$求对于每一个$a_i$是否存在$a_j$满足$a_i\&a_j=0$
   分析：同上一题一样，只需要记录一下转移从何处而来即可

4. E - Vowels
   题意：字符集大小为24，有n个单词，每个单词有三个字母，如果其中有一个元音，我们就称这个单词是合法的，元音的集合有$2^{24}$种可能，求这$2^{24}$种元音集合的正确单词数的平方的异或和。
   分析：现在的问题变成了 $a_i\&mask!=0$,我们注意到字母的个数很小，那么我们就可以使用容斥定理，求出一个字母的，两个字母，三个字母的贡献，然后进行$SOSdp$即可
   参考代码:code

5. Covering Sets CodeChef - COVERING
   题意: 给定集合$A,B,C$,定义运算$A(i),B(i),C(i)$，返回集合的第i个值(从0开始), 定义一个三元组$(\text{A}(i),\text{B}(j),\text{C}(k))$ 的并集为$i|j|k$,如果 $l\&(i|j|k)=l$,那么我们就称$(\text{A}(i),\text{B}(j),\text{C}(k))$ 覆盖 $l$，$R(l)$定义所有的覆盖 l的三元组的乘积的和即
   $$R(l)=\sum _{l\&(i|j|k)=l}A(i)\ast B(j)\ast C(k)$$
   求$R(0)+R(1)+R(2)+...R(2^N-1)$
   分析：直接枚举 $l$求满足的集合是不行的，我们可以统计每一个三元组$(\text{A}(i),\text{B}(j),\text{C}(k))$的贡献,我们发现它能够对 $t=2^{d(i|j|k)}$个$l$有贡献 ，所以我们统计所有的三元组，这样的复杂度过大，但是如果$i|j|k$相等的集合统一算贡献就可以了，对$A，B，C$都计算一次$SOSdp$, 然后我们就计算出了相乘，但是这样会有重复，我们需要减去$i|j|k$的真子集，把$SOSdp$倒着做一次即可
   参考代码：code

6. D. Jzzhu and Numbers给定 $a_1,..a_n$求有多少集合按位与的值为0
   参考代码： code1

7. COCI 2011/2012 Problem KOSARE给定$a_1,..{.}_n$ 求有多少个集合按位或为全集
   以上两题其实可以看做是一个题，先做一遍$SOSdp$求出 $F[mask]$，然后容斥
   参考代码：code2

8. hackrank subsets
   题意：
   操作1：在集合中插入一个元素
   操作2：在集合中删除一个元素
   操作3：查询集合中有多少个元素满足$a\&s=a$
   分析:
   我们用$bit(a)$表示$a$的二进制表示1的数量
   方法1：修改枚举前8位，查询枚举后八位，子集枚举复杂度 $O(Q\ast 8\ast 2^8)$
   $dp[i][j]$ 代表 $lo{w}_8\&i=lo{w}_8,hig{h}_8=j$的a个数
   修改的时候枚举包含前八位的集合
   查询的时候，枚举后八位的子集，前8位的子集就是 $dp[lo{w}_8]$
   方法2：维护3个数组$F,D,E$
   F: 维护的是$a$中$bit(a)>8)$，$F[i]$就是通常的$F[mask]$,即$mask\&a=a$
   D:维护的是$a$中$bit(a)\le 8$,$D[i]$是$a=i$的a的数量
   E:维护的是$a$中$bit(a)\le 8$,$E[mask]$是$mask\&a=mask$的数量
   修改操作

   1. $bit(a)\le 8$,修改$D,E$
   2. $bit(a)>8$,修改F，修改F就直接暴力修改，枚举所有包含$a\&mask=a$的集合
      查询操作
   3. $bit(s)\le 8$, 查询$D$即可，枚举$a$的所有子集
   4. $bit(s)>8$ ,$F[s]$为$bit(a)>8$的贡献，考虑怎么求$bit(a)\le 8$的贡献，我们对$s$取反得到$ss$,求$a\&ss!=0$的个数，这就变成了第4题
      参考代码code 1code2

9. Jersey Number
   题意:给定一个字符串，求有多少对区间有至少一个相同的字符
   分析：（icpc上这道题不能提交，数据是错的）先处理出来所有的区间的值，然后进行$SOSdp$即可
   参考代码：code

10. Beautiful Sandwich
    题意：给定一个字符串，字符集不超过18个，定义一个字符串的value 为 连续相同字符个数的平方，求每次删除几种字符后字符串的价值。
    分析：仔细想想其实和上一题有相似之处，平方我们可以拆开，$A\ast A={(1+...1)}_{A个1}\ast {(1+...1)}_{A个1}$,1代表一个字符出现一次，例如$abacaa$，我们考虑第一个a的贡献，从位置1开始，每次加入一个新的$a$，如果删除$b$，那么增加的值是$1(第一个a)\ast 1(第二个a)\ast 2$,如果删除$bc$,那么贡献就又增加了 $1\ast 2(第三个，第四个a)\ast 2$,这样就把贡献拆开，利用$SOSdp$来做
    参考代码：code,注意爆int

11. K. Pepsi Cola
    题意： 求 $2^N$子集合所有元素或的三次方
    分析：需要求出来每个值有多少个集合，采用$SOSdp$,需要搞懂第5题

12. Uchiha Brothers and Two Products

    题意：物品有两个属性，价值$p_i$和营养价值$a_i$，定义一个集合的营养价值为$\&a_i(i\in S)$,定义一个集合的价值为${\prod }_{i\in S}{p}_i$，给定营养价值$s$，取所有营养价值相同为s的集合的价值的和.
    分析：会发现营养价值这个条件就是$SOSdp$的内容，怎么将所有营养价值的和变成乘积，最后发现这个其实也是dp,比方说加入一个价值为b的$dp[i]=dp[i]+dp[i]\ast b+b$.将原本sosdp的内容修改即可，然后我们求出来$F[mask]$，依然要做一次反$SOSdp$

    参考代码：code

13. Strange Functions
    题意：给定$A[i]$,已知$$\begin{gathered} F[i]={A[i]}^2+\sum _{(i\&j)=jandj<i}G[j]{)}^2 \\ G[i]=\sum _{(i\&j)=jandj\le i}{(F[j])}^2 \end{gathered}$$
    分析: 老老实实按照$dp[mask][i]$来维护 $\sum G[i]$和$\sum {F[i]}^2$
    参考代码: code

14. D. Varying Kibibits
    题意：题意有些复杂，建议自己理解
    分析：怎么维护平方呢？不知道有没有做过线段树维护区间和平方那个题，就是维护一次项和二次项，怎么维护集合的平方呢？考虑再维护集合的个数即可，最后做一遍反 SOSdp即可
    参考代码:code