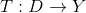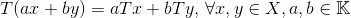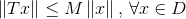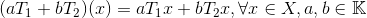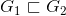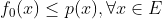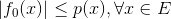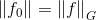1 有界线性算子
1.1 定义与性质
设X,Y是(统一数域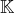

- 线性算子(齐次可加):
- 有界算子:存在常数M,使得
几个等价命题:
1.T一致连续;2.T连续;3.T在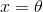
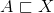
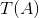
5.T有界;6.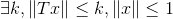
1.2 算子范数、算子空间
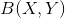

则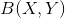
算子范数:
【如果Y是Banach空间,则B(X,Y)也是Banach空间。】

1.3 开映射、闭图像、共鸣定理
- open-mapping:设X,Y是Banach空间,
为有界线性算子,如果T(X)是Y中的第二纲集,则存在K>0,使得(满射)对于
使得
且有
【则对X中任一开集G,T(G)是Y中开集】
- 闭图像:设X,Y是Banach空间,
为闭算子,则T是有界的
- 共鸣(一致有界):设X是Banach空间,Y是赋范线性空间,
为有界线性算子。如果对于
,都有
,则
。

2 延拓与Hahn-Banach定理
2.1 延拓
设E是线性空间,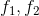
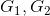
(1)
(2)
则称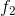
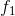

2.2 HBT
- 实:设G为实线性空间E的子空间,f是定义在G上的实线性泛函,p是定义在E上的次可加正齐泛函。f与p满足:
,则必存在定义在E上的实线性泛函
,满足(1)
;(2)
- 复:设G为复线性空间E的子空间,f是定义在G上的线性泛函,p是定义在E上的半范。f与p满足:
,则必存在定义在E上的实线性泛函
,满足(1)
;(2)
2.3 保范延拓
- 定理:设E是
空间,G是E的线性子空间,
是G上的有界线性泛函,则必存在E上的有界线性泛函
,满足:(1)
;(2)
- 推论:设E是
空间,G是E的线性子空间,
,若
,则存在E上的有界线性泛函f,使(1)
;(2)
- 【证明思路】构造f满足以上条件,令
,
显然其满足
,
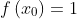
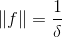
(1)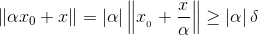
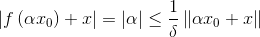
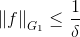
(2)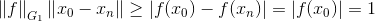
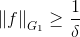
3 第二共轭空间 自然嵌入映射 自反空间
3.1 第二共轭空间
凸集分离定理
但是如果只满足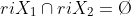
在C边界bdC上一点可以建立一个支撑超平面
参考文献:
[1]Hongxin Zhang 2007-06-21 State Key Lab of CAD&CG, ZJU