一、什么是Scara机器人?
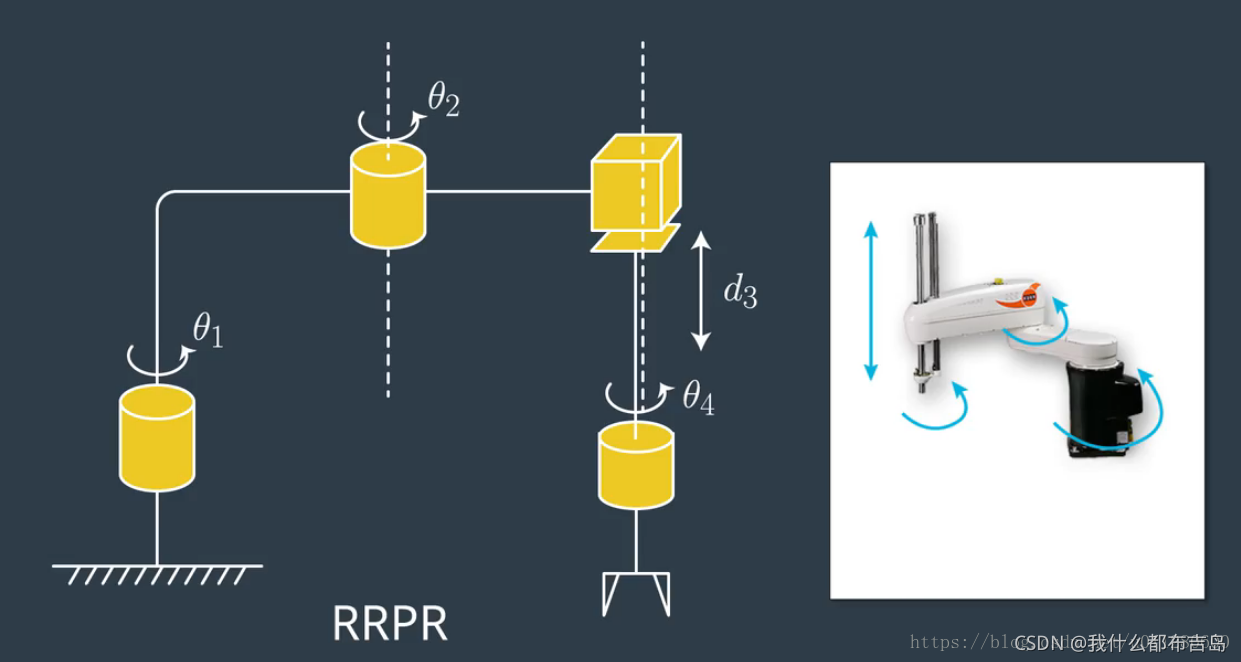
SCARA是Selective Compliance Assembly Robot Arm的缩写,意思是一种应用于装配作业的机器人手臂。它有3个旋转关节,最适用于平面定位。[1]
从图中可以看出Scara机器人共有四个关节,其结构是RRPR。
二、Scara机器人正解
MDH轴号是从1开始的,连杆编号则是从0开始,一个连杆一个坐标系,所以坐标系也是从0开始的。
Scara是一种常见的串联机器人,只需要按照一定步骤写出DH参数表即可得到正解。MDH参数建模步骤如下:
-
第一步,画出轴线的延长线(接下来都是相邻轴 i i i和 i + 1 i+1 i+1参照给出的);
-
第二步,若当前轴与下一轴有交点,交点作为连杆坐标系 { i } \{i\} {i}的原点;若平行,则任意公垂线与当前轴交点作为连杆坐标系 { i } \{i\} {i}的原点;若相异,唯一公垂线与当前轴交点作为连杆坐标系 { i } \{i\} {i}的原点;
-
第三步,令轴向与 Z ^ i \hat Z_i Z^i一致;
-
第四步,若当前轴与下一轴有交点,规定 X ^ i \hat X_i X^i为这两个轴的叉乘方向;若当前轴平行,随便选一个公垂线作为 X ^ i \hat X_i X^i;若为异面,仅有一个公垂线 X ^ i \hat X_i X^i;
-
第五步,右手法则给出 Y ^ i \hat Y_i Y^i;
Tips:从建模过程可以看出原点和 X ^ i \hat X_i X^i的方向可能不唯一,参数越简单越方便计算,一个切实有效的选取原则是:尽量使连杆参数为0。如,对于连杆坐标系 { 0 } \{0\} {0},当坐标系 { 1 } \{1\} {1}关节变量 θ 1 \theta_1 θ1为0时,连杆坐标系 { 0 } \{0\} {0} { 1 } \{1\} {1}完全重合!
- 延长线的画法最简单了,对于旋转关节轴线延长线是旋转轴,对于移动关节,则是运动方向(第一步完成);
- Scara机器人轴线延长线都是平行、重合关系,原点选取就有一定的弹性,为了尽可能减少参数书写(或者说让参数值为0),尽可能让 X X X轴共线,这样一来, d = 0 d=0 d=0;(第二步完成);
- 我们暂且规定向上为轴向,换句话说 Z Z Z轴都朝上;
- 这里所有的轴都是平行或者重合的,公垂线又过原点,所以确定了 X X X
- 右手法则,要不要都可以
这样我们就能写出我们想要的MDH参数表了:
| i i i | α i − 1 \alpha_{i-1} αi−1 | a i − 1 a_{i-1} ai−1 | d i d_i di | θ i \theta_i θi |
|---|---|---|---|---|
| 1 | 0 0 0 | 0 0 0 | 0 0 0 | θ 1 \theta_1 θ1 |
| 2 | 0 0 0 | l 1 l_1 l1 | 0 0 0 | θ 2 \theta_2 θ2 |
| 3 | 0 0 0 | l 2 l_2 l2 | − d 3 -d_3 −d3 | 0 0 0 |
| 4 | 0 0 0 | 0 0 0 | 0 0 0 | θ 4 \theta4 θ4 |
注:为什么 α \alpha α和 a a a的下表是轴号-1?答,因为这个过程发生在前一个轴。
根据
{
i
−
1
}
\{i-1\}
{i−1}变化到
{
i
}
\{i\}
{i}的一般表达式:
i
i
−
1
T
=
[
c
θ
i
−
s
θ
i
0
a
i
−
1
s
θ
c
α
i
−
1
c
θ
i
c
α
i
−
1
−
s
α
i
−
1
−
s
α
i
−
1
d
i
s
θ
i
s
α
i
−
1
c
θ
i
s
α
i
−
1
c
α
i
−
1
c
α
i
−
1
d
i
0
0
0
1
]
^{i-1}_iT=\begin{bmatrix} c\theta_i&-s\theta_i&0&a_{i-1}\\ s\theta c\alpha_{i-1}& c\theta_i c\alpha_{i-1}&-s\alpha_{i-1}&-s\alpha_{i-1}d_i\\ s\theta_{i} s\alpha_{i-1}&c\theta_i s\alpha_{i-1}&c\alpha_{i-1}&c\alpha_{i-1}d_i\\ 0&0&0&1 \end{bmatrix}
ii−1T=
cθisθcαi−1sθisαi−10−sθicθicαi−1cθisαi−100−sαi−1cαi−10ai−1−sαi−1dicαi−1di1
1
0
T
=
[
cos
θ
1
−
sin
θ
1
0
0
sin
θ
1
cos
θ
1
0
0
0
0
1
0
0
0
0
1
]
^0_1T= \begin{bmatrix} \cos\theta_1&-\sin\theta_1&0&0\\ \sin\theta_1&\cos\theta_1&0&0\\ 0&0&1&0\\ 0&0&0&1\\ \end{bmatrix}
10T=
cosθ1sinθ100−sinθ1cosθ10000100001
2
1
T
=
[
cos
θ
2
−
sin
θ
2
0
l
1
sin
θ
2
cos
θ
2
0
0
0
0
1
0
0
0
0
1
]
^1_2T= \begin{bmatrix} \cos\theta_2&-\sin\theta_2&0&l1\\ \sin\theta_2&\cos\theta_2&0&0\\ 0&0&1&0\\ 0&0&0&1\\ \end{bmatrix}
21T=
cosθ2sinθ200−sinθ2cosθ2000010l1001
3 2 T = [ 1 0 0 l 2 0 1 0 0 0 0 1 d 3 0 0 0 1 ] ^2_3T= \begin{bmatrix} 1&0&0&l_2\\ 0&1&0&0\\ 0&0&1&d_3\\ 0&0&0&1\\ \end{bmatrix} 32T= 100001000010l20d31
4 3 T = [ cos θ 4 − sin θ 4 0 0 sin θ 4 cos θ 4 0 0 0 0 1 0 0 0 0 1 ] ^3_4T= \begin{bmatrix} \cos\theta_4&-\sin\theta_4&0&0\\ \sin\theta_4&\cos\theta_4&0&0\\ 0&0&1&0\\ 0&0&0&1\\ \end{bmatrix} 43T= cosθ4sinθ400−sinθ4cosθ40000100001
Scara末端相对于基座标的旋转矩阵为:
4
0
T
=
1
0
T
2
1
T
3
2
T
4
3
T
=
[
cos
(
θ
1
+
θ
2
+
θ
4
)
−
sin
(
θ
1
+
θ
2
+
θ
4
)
0
l
2
cos
(
θ
1
+
θ
2
)
+
l
1
cos
θ
1
sin
(
θ
1
+
θ
2
+
θ
4
)
cos
(
θ
1
+
θ
2
+
θ
4
)
0
l
2
sin
(
θ
1
+
θ
2
)
+
l
1
sin
θ
1
0
0
1
d
3
0
0
0
1
]
(5)
^0_4T=^0_1T^1_2T^2_3T^3_4T=\begin{bmatrix} \cos(\theta_1 + \theta_2 + \theta_4)& -\sin(\theta_1 + \theta_2 + \theta_4)& 0& l_2\cos(\theta_1 + \theta_2) + l_1\cos\theta_1\\ \sin(\theta_1 + \theta_2 + \theta_4)& \cos(\theta_1 + \theta_2 + \theta_4)& 0& l_2\sin(\theta_1 + \theta_2 )+ l_1\sin\theta_1\\ 0& 0& 1& d_3\\ 0& 0& 0& 1\\ \end{bmatrix}\tag{5}
40T=10T21T32T43T=
cos(θ1+θ2+θ4)sin(θ1+θ2+θ4)00−sin(θ1+θ2+θ4)cos(θ1+θ2+θ4)000010l2cos(θ1+θ2)+l1cosθ1l2sin(θ1+θ2)+l1sinθ1d31
(5)
三、Scara机器人逆解
3.1 代数解法
代数解法无非就是利用三角恒等式进行变换,最后通过求解超越方程(也就是带有三角函数的方程?)得到逆解。
先求解
θ
2
\theta_2
θ2,式子(1)的结果告诉我们,该机构姿态等效于一个绕
Z
Z
Z旋转的角度,因此:
4
0
T
=
[
cos
(
θ
1
+
θ
2
+
θ
4
)
−
sin
(
θ
1
+
θ
2
+
θ
4
)
0
l
2
cos
(
θ
1
+
θ
2
)
+
l
1
cos
θ
1
sin
(
θ
1
+
θ
2
+
θ
4
)
cos
(
θ
1
+
θ
2
+
θ
4
)
0
l
2
sin
(
θ
1
+
θ
2
)
+
l
1
sin
θ
1
0
0
1
d
3
0
0
0
1
]
(5)
^0_4T=\begin{bmatrix} \cos(\theta_1 + \theta_2 + \theta_4)& -\sin(\theta_1 + \theta_2 + \theta_4)& 0& l2\cos(\theta_1 + \theta_2) + l1\cos\theta_1\\ \sin(\theta_1 + \theta_2 + \theta_4)& \cos(\theta_1 + \theta_2 + \theta_4)& 0& l2\sin(\theta_1 + \theta_2 )+ l1\sin\theta_1\\ 0& 0& 1& d_3\\ 0& 0& 0& 1\\ \end{bmatrix}\tag{5}
40T=
cos(θ1+θ2+θ4)sin(θ1+θ2+θ4)00−sin(θ1+θ2+θ4)cos(θ1+θ2+θ4)000010l2cos(θ1+θ2)+l1cosθ1l2sin(θ1+θ2)+l1sinθ1d31
(5)
令
ϕ
=
θ
1
+
θ
2
+
θ
4
\phi=\theta_1+\theta_2+\theta_4
ϕ=θ1+θ2+θ4,(5)可以写成:
[
cos
ϕ
−
sin
ϕ
0
x
sin
ϕ
cos
ϕ
0
y
0
0
1
z
0
0
0
1
]
(6)
\begin{bmatrix} \cos\phi&-\sin\phi&0&x\\ \sin\phi&\cos\phi&0&y\\ 0&0&1&z\\ 0&0&0&1 \end{bmatrix}\tag{6}
cosϕsinϕ00−sinϕcosϕ000010xyz1
(6)
令(5)(6)矩阵相等,有:
cos
ϕ
=
c
o
s
(
θ
1
+
θ
2
+
θ
4
)
(7)
\cos\phi=cos(\theta_1+\theta_2+\theta_4)\tag{7}
cosϕ=cos(θ1+θ2+θ4)(7)
sin
ϕ
=
s
i
n
(
θ
1
+
θ
2
+
θ
4
)
(8)
\sin\phi=sin(\theta_1+\theta_2+\theta_4)\tag{8}
sinϕ=sin(θ1+θ2+θ4)(8)
x
=
l
1
cos
θ
1
+
l
2
cos
(
θ
1
+
θ
2
)
(9)
x=l_1\cos\theta_1+l_2\cos(\theta_1+\theta_2)\tag{9}
x=l1cosθ1+l2cos(θ1+θ2)(9)
y
=
l
1
sin
θ
1
+
l
2
sin
(
θ
1
+
θ
2
)
(10)
y=l_1\sin\theta_1+l_2\sin(\theta_1+\theta_2)\tag{10}
y=l1sinθ1+l2sin(θ1+θ2)(10)
为了方便查看我们令
s
1
=
sin
θ
1
s_1=\sin\theta_1
s1=sinθ1,
c
1
=
cos
θ
2
c_1=\cos\theta_2
c1=cosθ2,
s
12
=
sin
(
θ
1
+
θ
2
)
s_{12}=\sin(\theta_1+\theta_2)
s12=sin(θ1+θ2),
c
12
=
cos
(
θ
1
+
θ
2
)
c_{12}=\cos(\theta_1+\theta_2)
c12=cos(θ1+θ2),(9)(10)可以写成:
x
=
l
1
c
1
+
l
2
c
o
s
12
(11)
x=l_1c_1+l_2cos_{12}\tag{11}
x=l1c1+l2cos12(11)
y
=
l
1
s
1
+
l
2
s
12
(12)
y=l_1s_1+l_2s_{12}\tag{12}
y=l1s1+l2s12(12)
对(11)(12)式子平方后求和有:
x
2
+
y
2
=
l
1
2
+
l
2
2
+
2
l
1
l
2
c
2
(13)
x^2+y^2=l_1^2+l_2^2+2l_1l_2c_2\tag{13}
x2+y2=l12+l22+2l1l2c2(13)
上面用到了三角函数同角度正余弦平方和等于1,和
sin
(
a
+
b
)
\sin(a+b)
sin(a+b)、
cos
(
a
+
b
)
\cos(a+b)
cos(a+b)。
因为
l
1
l_1
l1
l
2
l_2
l2不为零,所以有:
cos
θ
2
=
x
2
+
y
2
−
l
1
2
−
l
2
2
2
l
1
l
2
(13)
\cos\theta_2=\frac {x^2+y^2-l_1^2-l_2^2}{2l_1l_2}\tag{13}
cosθ2=2l1l2x2+y2−l12−l22(13)
上述方程有解的条件是,(2)右边等式的取值范围为[-1,1]。如果约束条件不满足,那么说明该点位于工作空间外(够不着)。
如果点位于工作空间内 ,那么有:
s 2 = ± 1 − c 2 2 (14) s_2= \pm\sqrt{1-c_2^2}\tag{14} s2=±1−c22(14)
利用双参数反正切函数atan可以轻松得到
θ
2
\theta_2
θ2:
θ
2
=
a
t
a
n
2
(
s
2
,
c
2
)
(15)
\theta_2=atan2(s_2,c_2)\tag{15}
θ2=atan2(s2,c2)(15)
PS:为什么不直接将(2)求反正切?原因有三个:
- atan2的值域 [ − π , π ] [-\pi,\pi] [−π,π]刚好是一个圆周,而acos值域为 [ 0 , π ] [0,\pi] [0,π],asin值域为 [ − π 2 , π 2 ] [-\frac{\pi}{2},\frac{\pi}{2}] [−2π,2π],如果你使用后面两种,为了支持圆周范围的角度,你需要额外加上周期;
- 数值上,atan2误差更加小[2]
求取
θ
1
\theta_1
θ1较为麻烦,将(11)(12)进行拆分后重新组合有:
x
=
k
1
−
k
2
s
1
(16)
x=k_1-k_2s1\tag{16}
x=k1−k2s1(16)
y = k 1 s 1 + k 2 s 2 (17) y=k_1s_1+k_2s_2\tag{17} y=k1s1+k2s2(17)
其中
k
1
=
l
1
+
l
2
c
2
k_1=l_1+l_2c_2
k1=l1+l2c2
k
2
=
l
2
s
2
k_2=l_2s_2
k2=l2s2,这里的小技巧是将
k
1
k_1
k1
k
2
k_2
k2想象成三角形的两个直角边,他们的斜边为
r
=
+
k
1
2
+
k
2
2
r=+\sqrt{k_1^2+k_2^2}
r=+k12+k22,夹角为
γ
=
a
t
a
n
2
(
k
2
,
k
1
)
\gamma=atan2(k_2,k_1)
γ=atan2(k2,k1)利用
r
r
r和
γ
\gamma
γ有:
k
1
=
r
cos
γ
k
2
=
r
sin
γ
(18)
k_1=r\cos\gamma\\k_2=r\sin\gamma\tag{18}
k1=rcosγk2=rsinγ(18)
于是(16)(17)可以写成:
x
r
=
cos
γ
cos
θ
1
−
sin
γ
sin
θ
1
x
r
=
cos
γ
sin
θ
1
+
sin
γ
cos
θ
1
(19)
\frac{x}{r}=\cos\gamma\cos\theta_1-\sin\gamma\sin\theta_1\\ \frac{x}{r}=\cos\gamma\sin\theta_1+\sin\gamma\cos\theta_1\tag{19}
rx=cosγcosθ1−sinγsinθ1rx=cosγsinθ1+sinγcosθ1(19)
继续化简:
x
r
=
cos
(
θ
1
+
θ
2
)
y
r
=
sin
(
θ
1
+
θ
2
)
(20)
\frac{x}{r}=\cos(\theta_1+\theta_2)\\ \frac{y}{r}=\sin(\theta_1+\theta_2)\tag{20}
rx=cos(θ1+θ2)ry=sin(θ1+θ2)(20)
利用反正切公式有:
γ
+
θ
1
=
a
t
a
n
(
y
,
x
)
\gamma+\theta_1=atan(y,x)
γ+θ1=atan(y,x)
从而得到
θ
1
=
a
t
a
n
2
(
y
,
x
)
−
a
t
a
n
2
(
k
2
,
k
1
)
(21)
\theta_1=atan2(y,x)-atan2(k_2,k_1)\tag{21}
θ1=atan2(y,x)−atan2(k2,k1)(21)
因为
k
2
k_2
k2
k
1
k_1
k1只与
θ
2
\theta_2
θ2有关,而
θ
2
\theta_2
θ2已知,所以,
θ
1
\theta_1
θ1可求,结合(7)(8)可以求得
θ
1
+
θ
2
+
θ
4
\theta_1+\theta_2+\theta_4
θ1+θ2+θ4的和,而
θ
1
\theta_1
θ1
θ
2
\theta_2
θ2已知,故有
θ
4
=
a
t
a
n
(
sin
ϕ
,
cos
ϕ
)
(22)
\theta_4=atan(\sin\phi,\cos\phi)\tag{22}
θ4=atan(sinϕ,cosϕ)(22)
因为只有第三个轴影响
Z
Z
Z轴,所以
d
3
=
z
d_3=z
d3=z
3.2 几何解法
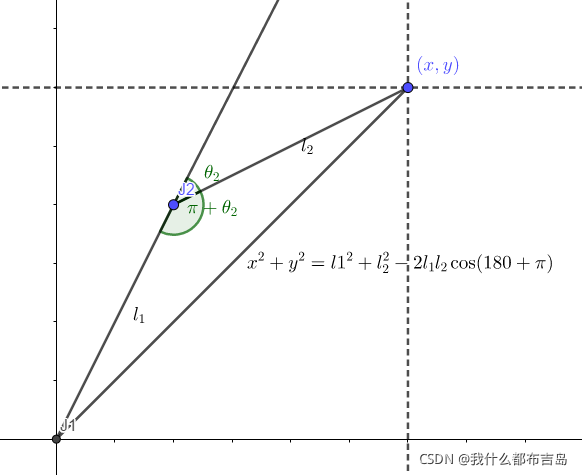
这种方法是将空间几何参数分解为若干个平面几何问题,这种方法在求解许多操作臂(尤其是 α \alpha α为0或90度时)相当容易。画出机器人的俯视图(上三角构型)如下:
J3所在的位置时机械手末端位置,根据余弦定理有:
x
2
+
y
2
=
l
1
2
+
l
2
2
−
2
l
1
l
2
c
o
s
(
π
+
θ
2
)
(23)
x^2+y^2=l_1^2+l_2^2-2l_1l_2cos(\pi+\theta_2)\tag{23}
x2+y2=l12+l22−2l1l2cos(π+θ2)(23)
整理有:
c
2
=
x
2
+
y
2
−
l
1
2
−
l
2
2
2
l
1
l
2
(24)
c_2=\frac{x^2+y^2-l_1^2-l_2^2}{2l_1l_2}\tag{24}
c2=2l1l2x2+y2−l12−l22(24)
上图所示的三角可以看出,
θ
2
∈
[
π
,
0
]
\theta_2 \in[\pi,0]
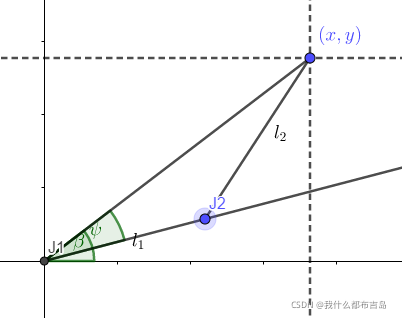
θ2∈[π,0],特别注意在此之前验证两边之和大于第三边这个约束。再来看下三角情况:
根据对称关系,容易得到另一种三角构型,
θ
2
′
=
−
θ
2
\theta_2^{\prime}=-\theta_2
θ2′=−θ2。下面求解
θ
1
\theta_1
θ1:
记
X
X
X轴到第一条臂的角度为
β
\beta
β,到两条臂的对边角度为
ψ
\psi
ψ,对于
β
\beta
β,由反正切公式容易得出:
β
=
a
t
a
n
2
(
y
,
x
)
(25)
\beta=atan2(y,x)\tag{25}
β=atan2(y,x)(25)
利用余弦定理:
cos
ψ
=
x
2
+
y
2
+
l
1
2
+
l
2
2
2
l
1
x
2
+
y
2
(26)
\cos\psi=\frac{x^2+y^2+l_1^2+l_2^2}{2l_1\sqrt{x^2+y^2}}\tag{26}
cosψ=2l1x2+y2x2+y2+l12+l22(26)
其中
ψ
∈
[
0
,
π
]
\psi\in[0,\pi]
ψ∈[0,π],注意我们需要确保一组变量满足几何关系才能使用这些定理。显然:
θ
1
=
β
±
ψ
(27)
\theta_1=\beta\pm\psi\tag{27}
θ1=β±ψ(27)
当
θ
2
>
0
\theta_2\gt0
θ2>0取负数,对应下三角图;当
θ
2
<
0
\theta_2\lt0
θ2<0取正数,对应上三角图。这种构型非常特殊,姿态角等于前三关节的和,对于逆解,我们已知姿态角
ϕ
:
\phi:
ϕ:
ϕ
=
θ
1
+
θ
2
+
θ
4
(28)
\phi=\theta_1+\theta_2+\theta_4\tag{28}
ϕ=θ1+θ2+θ4(28)
即:
θ
3
=
ϕ
−
θ
1
−
θ
4
(29)
\theta_3=\phi-\theta_1-\theta_4\tag{29}
θ3=ϕ−θ1−θ4(29)
因为只有第三个轴影响
Z
Z
Z轴,所以
d
3
=
z
(30)
d_3=z\tag{30}
d3=z(30)
2.3 机器人逆解小结
求解机器人逆解的时候常常都是在带三角函数的超越方程,求解超越方程的基本方法是变量代换,如上面角度合并到同一个三角函数中;其实,另一种求解逆解方便的方法是将三角函数通过万能公式转换成多项式,通过求解小于五阶的多项式间接求解。万能变换:
u
=
tan
θ
2
cos
θ
=
1
−
u
2
1
+
u
2
sin
θ
=
2
u
1
+
u
2
u=\tan\frac{\theta}{2}\\ \cos\theta=\frac{1-u^2}{1+u^2}\\ \sin\theta=\frac{2u}{1+u^2}
u=tan2θcosθ=1+u21−u2sinθ=1+u22u
[1]https://baike.baidu.com/item/SCARA/5158742?fr=aladdin
[2]https://blog.csdn.net/maple_2014/article/details/104594261
[3] John J. Craig, 贠超. 机器人学导论[M]. 机械工业出版社, 2006.