本节通过一个向量向线和平面投影,引出了投影向量和误差向量概念。误差向量表示空间中两个向量的差异的手段,其模的大小是误差量化的手段,模越大,误差越大。一个子空间有一个仅与自身有关的投影矩阵 P P P ,空间中任意向量都可以通过这个 P P P 求得投影和“偏差”大小。
引出投影向量和误差向量的概念是我们理解最小二乘解的关键,最小二乘法中的“最小”指的是误差向量最小。空间中两个向量只要不共线,一个向量就可以分解成另一个向量共线部分和剩余部分,最常见的一种方式就是“投影”,投影就是以一定的角度分解原向量,分解之后两个分量相互正交。这是一种非常特殊的一种分解,也是最符合人类习惯的一种方式。
一个不在某个子空间上的向量,是无法用某个子空间线性表示的。前面我们学习了很多求取向量在子空间的精确解的方法,但是对于子空间外的向量确无能为力。如果我们在子空间上找一个“差不多”的向量,进行近似表达这个向量,近似后的向量可以用子空间精确表达,对于原问题来说,这是近似的,但是对于子空间来说却是精确的。
根据三角形法则,将原向量分解为子空间上的向量和指向原向量终点向量。后者叫做误差向量,这个误差向量的大小可用来衡量近似的程度,误差向量的模越小,说明近似得越好,反之则越差。
那么什么样的分解是一个可以让误差尽可能小呢?投影!分解为正交于子空间向量和投影向量,这是根据经验得出的,一个向量上的点到直线最接近的方法是作垂线,一个向量到平面最接近的方法也是做垂涎,那么对于任意维度的子空间是不是正交是接近的。
对于原来的不在子空间上的向量左乘某个矩阵使得其分解为垂直子空间和在子空间上的向量的矩阵,称为投影矩阵。事实上,子空间上的投影是将一个更高维度的向量用子空间近似表示,获取近似向量的方法是通过投影矩阵。可见投影矩阵和要表示的向量的维数是有关系的,与向量矩阵的方向和大小是无关的。
一、子空间维数为1
向量减法的方向指向被减向量。
假设子空间是向量
a
\mathbf{a}
a ,所有能够表示的列空间是:
p
=
x
a
(
x
∈
R
)
(1)
\mathbf{p}=x\mathbf{a}\quad (x\in \mathbb{R})\tag{1}
p=xa(x∈R)(1)
其中
x
x
x 是一个实数。
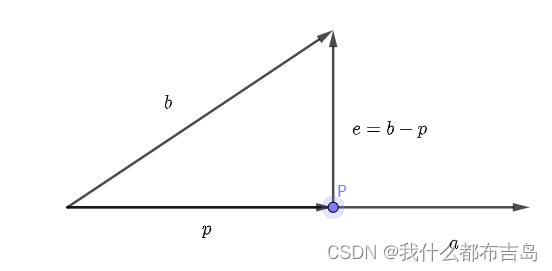
对于一个不属于其列空间的向量
b
\mathbf{b}
b,我们无法找到一个实数
x
x
x 用于表达这个向量,但是我们能够找到与之最接近的向量
p
\mathbf{p}
p 用于近似表示,这种近似表示是存在误差的,这个误差由近似表示的向量末端指向原来待表示向量:
e
=
b
−
p
(2)
\mathbf{e}=\mathbf{b}-\mathbf{p}\tag{2}
e=b−p(2)
从中学我们就知道点到直线最短距离为垂足,这个用于表示误差的向量
e
\mathbf{e}
e 模大小表示误差程度。这样正交关系使得:子空间
a
\mathbf{a}
a 与误差向量
e
\mathbf{e}
e 正交。
a
T
e
=
a
T
(
b
−
p
)
=
a
T
(
b
−
x
a
)
=
0
(3)
\mathbf{a}^T\mathbf{e}=\mathbf{a}^T(\mathbf{b}-\mathbf{p})=\mathbf{a}^T(\mathbf{b}-x\mathbf{a})=0\tag{3}
aTe=aT(b−p)=aT(b−xa)=0(3)
这样用来近似表示
p
\mathbf{p}
p 的线性组合就是我们的近似解。对
(
3
)
(3)
(3) 化简有:
x
=
a
T
b
a
T
a
(4)
x=\frac{\mathbf{a}^T\mathbf{b}}{\mathbf{a}^T\mathbf{a}}\tag{4}
x=aTaaTb(4)
对于任意向量
p
\mathbf{p}
p:
p
=
x
a
=
a
T
b
a
T
a
a
(5)
p=x\mathbf{a}=\frac{\mathbf{a}^T\mathbf{b}}{\mathbf{a}^T\mathbf{a}}\mathbf{a}\tag{5}
p=xa=aTaaTba(5)
因为
x
x
x 是一个数,所以:
p
=
x
a
=
a
a
T
b
a
T
a
(6)
p=x\mathbf{a}=\mathbf{a}\frac{\mathbf{a}^T\mathbf{b}}{\mathbf{a}^T\mathbf{a}}\tag{6}
p=xa=aaTaaTb(6)
假如我们将向量 b \mathbf{b} b 翻倍,那么投影向量 p \mathbf{p} p也将翻倍;假如向量 a \mathbf{a} a 翻倍或者反向,你会发现投影 p \mathbf p p 不会改变,它仍然是原投影向量。
在线性代数中我们称矩阵
P
P
P为投影矩阵,其的数值等于:
P
=
a
a
T
a
T
a
(7)
P=\frac{aa^T}{a^Ta}\tag{7}
P=aTaaaT(7)
于是经过FIxed 之后的近似向量以写成:
P
r
o
j
p
=
P
b
(8)
Proj_p=Pb\tag{8}
Projp=Pb(8)
可以看出,投影矩阵只与目标子空间情况有关,一旦子空间确定,所有向量都能通过投影矩阵映射到子空间上。投影矩阵有一些什么性质呢?
- 投影矩阵是一个对称矩阵,即 P T = P P^T=P PT=P;
- 投影矩阵的列空间是一个经过 a a a 向量的直线(因为是直线,所以 C ( P ) C(P) C(P) 的秩为1);
- 对一个向量执行多次投影等效于只执行1次;
为什么投影矩阵是一个对称矩阵?因为 A A T AA^T AAT一定是一个对称矩阵。证明: ( A A T ) T = A T T A T = A A T (AA^T)^T={A^T}^TA^T=AA^T (AAT)T=ATTAT=AAT,转置等于其本身,符合对称矩阵定义。
为什么投影矩阵的列空间是一个直线? P b = p Pb=p Pb=p 从方程角度上看,输入向量 b b b 是未知数,结果是投影,也就是结果向量,从上面分析来看,它的结果只能是与 a a a 共线的直线,换句话说列空间秩与子空间相同。
为什么 P 2 = P P^2=P P2=P 计算一下便知,长度是可以消去的。
二、子空间维数为2
设子空间由两个基
a
1
a_1
a1 和
a
2
a_2
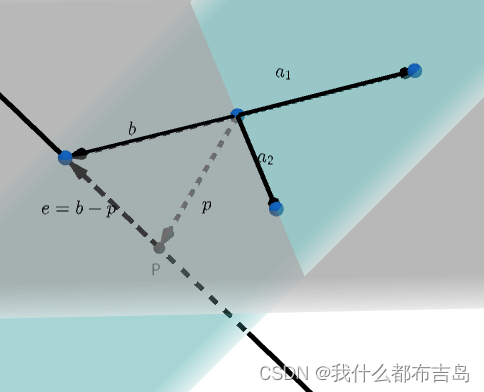
a2 组成,这两个基的线性组合分布在一个平面内,但是我们仍然希望能用这两个基近似表示。如下图:
子空间外的向量
b
b
b 通过投影的方式获取一个投影向量
p
p
p ,因为
p
∈
C
(
A
)
p\in C(A)
p∈C(A),所以:
A
x
^
=
p
(9)
A\hat{x}=p\tag{9}
Ax^=p(9)
对应的误差向量
e
e
e:
e
=
b
−
p
(10)
e=b-p\tag{10}
e=b−p(10)
因为误差向量垂直于子空间
C
(
A
)
C(A)
C(A),所以:
A
T
(
b
−
A
x
^
)
=
0
(11)
A^T(b-A\hat x)=0\tag{11}
AT(b−Ax^)=0(11)
整理得:
x
^
=
(
A
T
A
)
−
1
A
T
b
(12)
\hat x=(A^TA)^{-1}A^Tb\tag{12}
x^=(ATA)−1ATb(12)
定义投影矩阵
P
P
P:
P
=
A
(
A
T
A
)
−
1
A
T
(13)
P=A(A^TA)^{-1}A^T\tag{13}
P=A(ATA)−1AT(13)
这样一来,所有不属于子空间的向量都可以得到一个在子空间的近似向量:
p
=
P
b
(14)
p=Pb\tag{14}
p=Pb(14)
思考下面变换是否成立: P = A ( A T A ) − 1 A T = A A − 1 ( A T ) − 1 A T = I P=A(A^TA)^{-1}A^T=AA^{-1}(A^T)^{-1}A^T=I P=A(ATA)−1AT=AA−1(AT)−1AT=I
答案是否定的,因为 A A A不一定是可逆的。可逆的基本条件是他必须是一个方阵,且列和行都是满秩的。
假如 A A A确实是一个可逆矩阵,那么列空间将是整个 n n n维空间,投影矩阵 P = I P=I P=I。
一个矩阵的乘以其转置只能说明他是一个对称矩阵 A T A A^TA ATA,忘记了可以复习对称矩阵:https://blog.csdn.net/weixin_39258979/article/details/110306510
平面投影同样满足:
- P T = P P^T=P PT=P
- P 2 = P P^2=P P2=P
三、最小二乘法直线拟合
最小二乘法拟合直线(Least square fitting by a line)。
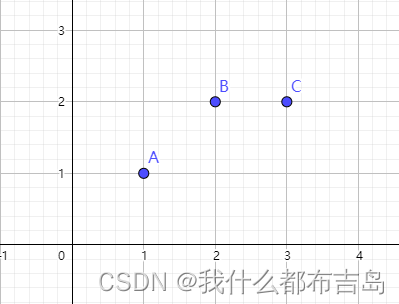
求一个经过
A
(
1
,
1
)
A(1,1)
A(1,1)
B
(
2
,
2
)
B(2,2)
B(2,2)
C
(
3
,
2
)
C(3,2)
C(3,2)的直线方程:
b
=
C
+
D
t
b=C+Dt
b=C+Dt
将点代入方程有:
C
+
D
=
1
C
+
2
D
=
2
C
+
3
D
=
2
C+D=1\\ C+2D=2\\ C+3D=2
C+D=1C+2D=2C+3D=2
写成矩阵形式:
[
1
1
1
2
1
3
]
[
C
D
]
=
[
1
2
2
]
\begin{bmatrix} 1&1\\1&2\\1&3 \end{bmatrix}\begin{bmatrix} C\\D \end{bmatrix}=\begin{bmatrix}1\\2\\2\end{bmatrix}
111123
[CD]=
122
记:
A
=
[
1
1
1
2
1
3
]
X
=
[
C
D
]
b
=
[
1
2
2
]
A=\begin{bmatrix} 1&1\\1&2\\1&3 \end{bmatrix}\quad X=\begin{bmatrix} C\\D \end{bmatrix}\quad b=\begin{bmatrix}1\\2\\2\end{bmatrix}
A=
111123
X=[CD]b=
122
A
X
=
b
AX=b
AX=b是无解的,因为
A
A
A是一个“瘦”子矩阵(方程组个数大于未知数),为了继续求解一个最优解,我们将等式两边同时乘以
A
T
A^T
AT:
A
T
A
x
^
=
A
T
b
A^TA\hat x=A^Tb
ATAx^=ATb
下节课将继续这个求解。