一维信号短时傅里叶变换域邻域降噪方法（MATLAB）

噪声在人类日常生活中无处不在,其会降低语音信号的质量和可懂度。在低信噪比的恶劣环境中,这种负面影响愈发严重。为了解决这个问题,众多研究人员在过去的几十年里提出了许多降噪算法。

根据原理的不同,降噪算法可大致分为五类:谱减法、最优滤波法、基于统计模型的方法、子空间方法、以及基于机器学习的方法。其中,最优滤波法是较为常用的一类,其将降噪问题转化为最优滤波器的设计问题。根据采用麦克风数量的不同,降噪算法又可分为单通道和多通道两类。此外,根据处理噪声信号的域,这些算法可以分为时域和变换域(如短时傅里叶变换域降噪算法。虽然这些方法已经取得了一定程度上的成功,但降噪仍然是一项具有挑战性的任务。基于相邻帧STFT系数互不相关的假设,早期的STFT域最优降噪方法绝大多数都是滤波增益,即每个频点的滤波器长度为1。然而,由于语音降噪时,语音帧需要有相互重叠,并且语音信号本身是强自相关的,所以当前帧的STFT系数与相邻帧的STFT系数高度相关。基于帧间相关性的不可忽略性,可推导出一组最优滤波器。

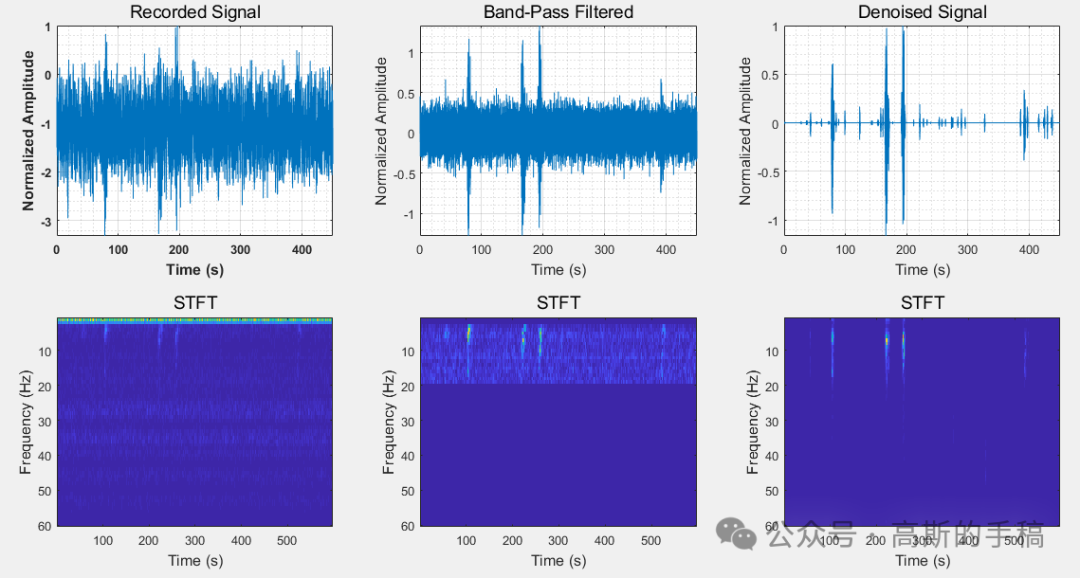
鉴于此，采用短时傅里叶变换域邻域降噪方法对一维信号进行降噪，运行环境为MATLAB 2021B。

[DD,DDT,DDTDD] = defDDt(N); % 2d Order difference operators.

    for k = 1:Nit
        u_old = u;
        
        %% u sub-problem %%
        % Solves a linear system using the conjugate gradient method.
        [u,~] = cgs(rho*DDTDD + lam*speye(N),lam*f+rho*DDT*(v - mu/rho),1e-5,100);
        
        %% v sub-problem %%
        x    = DD*u + mu/rho;
        v    = shrink(x, 1/rho);
        
       %% Update Lagrange multiplier
        mu   = mu + (DD*u - v);
        
        r1   = u - f;
        funcVal(k) = (lam/2)*norm(r1,'fro')^2 + sum(v(:));
    
    end
    
    out.sol = u;
    out.funVal = funcVal(1:k);

end

function [DD,DDT,DDTDD] = defDDt(N)
%Create a first order difference matrix D
e = ones(N,1);
B = spdiags([e -e], [1 0], N, N);
B(N,1) =  1;

D = B; 
clear B;
DD = D*D;
clear D;
% Create the transpose of D
DDT = DD'; %Remember that DT = -D, also called the backward difference.
DDTDD = DD'*DD;
end

function z = shrink(x,r)
z = sign(x).*max(abs(x)- r,0);
end


完整代码：https://mbd.pub/o/bread/ZJyTl5lq
擅长领域：现代信号处理，机器学习，深度学习，数字孪生，时间序列分析，设备缺陷检测、设备异常检测、设备智能故障诊断与健康管理PHM等。

擅长领域：现代信号处理，机器学习，深度学习，数字孪生，时间序列分析，设备缺陷检测、设备异常检测、设备智能故障诊断与健康管理PHM等。

一维信号短时傅里叶变换域邻域降噪方法（MATLAB）

悦读