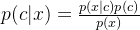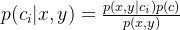条件概率
假设现在有一个装了7块石头的罐子(3块灰色,4块黑色),如果从中随机取出一块,灰色的可能性就是3/7,黑色的可能性是4/7。我们使用p(gray)来表示取到灰色石头的概率,其概率值可以通过灰色石头数目除以总的石头数目来得到。
如果石头放在两个桶中,其中A桶中2灰2黑,B桶中1灰2黑,那么概率该怎么计算?要计算P(gray)或者P(black),事先得知道石头所在桶的信息会不会改变结果?我们可以想到计算从B桶中取到灰色石头的概率的办法,这就是所谓的条件概率。
假定计算的是从B桶取到灰色石头的概率,这个概率记为P(gray|bucketB),我们称之为“在已知石头出自B桶的情况下,取出灰色石头的概率”。所以P(gray|bucketA)为2/4,P(gray|bucketB)为1/3。
条件概率的计算公式如下:
P(gray|bucketB)=P(gray and bucketB)/P(bucketB)。
另一种有效计算条件概率的方法被称为贝叶斯准则。贝叶斯准则告诉我们如何交换条件概率中的条件与结果,即如果已知P(x|c),要求P(c|x),那么可以使用下面的计算方法:
使用条件概率来分类
我们可以使用贝叶斯准则来交换概率中的条件与结果。具体的,应用贝叶斯准则得到:
使用这些定义,可以定义贝叶斯分类准则为:
如果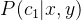
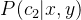
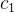
如果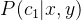
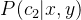
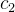
使用贝叶斯准则,可以通过已知的三个概率值来计算未知的概率值。