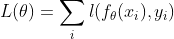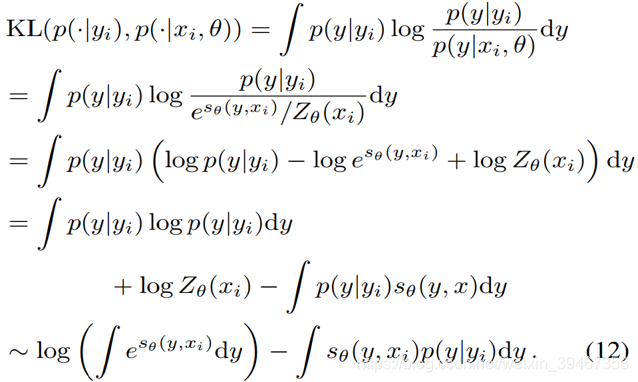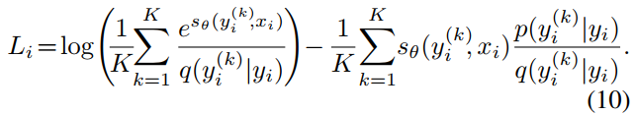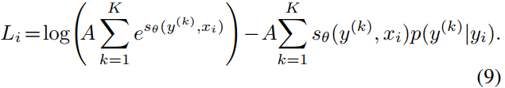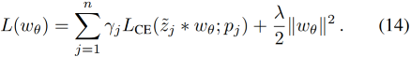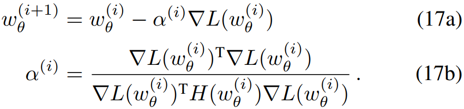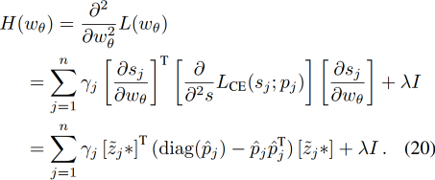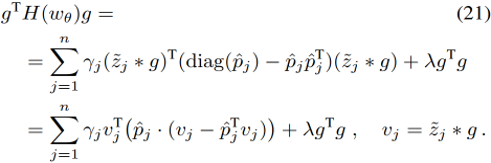Martin大神在CVPR2020的又一跟踪作,快来欣赏:
代码地址:pytracking-master 预训练好的网络地址:prdimp50.pth.tar
将目标跟踪视为每一帧的目标回归问题:
1、使用DCF或Siamese等进行粗略定位,其对于目标背景、杂波和遮挡具有一定鲁棒性【Target Center Regression】;
2、使用单独的网络分支,用于回归目标框【Bounding Box Regression】。
发现问题:
1、大多数跟踪方法关注于目标框中心坐标(即定义为目标的质心)的回归。图中,由于目标外观的微小变化,导致GT框的中心位置发生严重偏移,故而目标中心回归是一项艰巨任务。
2、对GT边界框未进行准确标注,而在训练网络时,标注的这种分歧变化会被忽略。多个注释者对给定对象的注释有所差异,尤其出现运动模糊、遮挡、小目标等情况下尤为明显,所以准确的bbox标签也是一项艰巨任务。
提出方法:
对输入的图像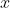
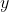

回归问题:
对于映射函数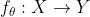
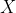
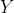
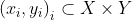
1)直接回归法
定义损失函数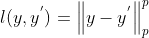
特点:虽在光流法、深度估计等小有成就。但在目标检测与跟踪、人体姿态估计不太适用。
2)置信度预测回归法
定义置信度回归函数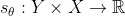
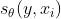
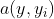
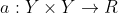
定义损失函数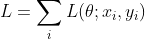
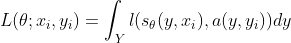
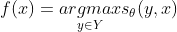
特点:以预测的置信度值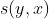
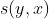
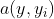
置信度预测回归相比直接回归的优点:
1,在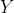
2、前者更能轻松利用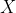
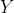
Loss的计算
在本文中,作者计算GT分布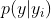
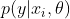
对于公式(8),作者提出了两种方法来近似:
1)网格采样
通过评估CNN在y处的输出得到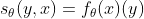
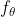
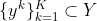

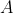

特点:该方法不能很好的缩放到更高的维度,而且刚性网格会引起采样偏差
2)蒙特卡洛积分
其中,
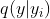
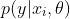
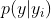
特点:需要对网络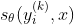
回归训练
1)TCR目标中心回归:
由于网络为全卷积,故采用网格采样近似与
的KL散度。
简单地,设,得到
定义Loss:
与DiMP推导不同,作者在最速下降公式中,用二次牛顿法代替高斯牛顿法:
其中,
由链式法则可得: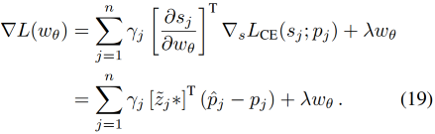
那么公式(17b)的分母可以表示为:
2)BBR目标框回归:
对进行积分以建立bbox标签中的噪声和不确定模型,利用蒙特卡洛积分最小化KL散度【文献18表明,以anno

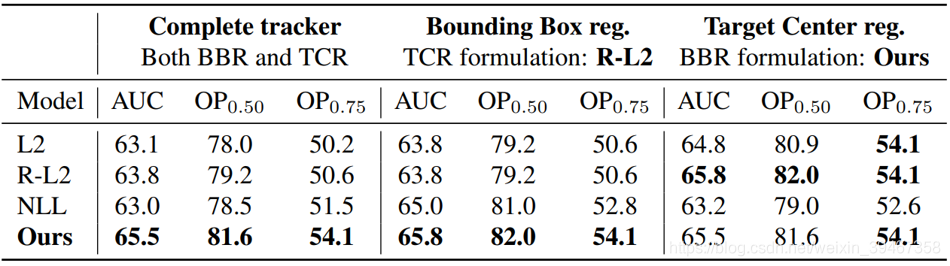
回归方法比较
L2:使用DiMP中BBR的标准平方损失
R-L2:使用DiMP中TCR的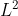
NLL:最小化的负对数似然函数
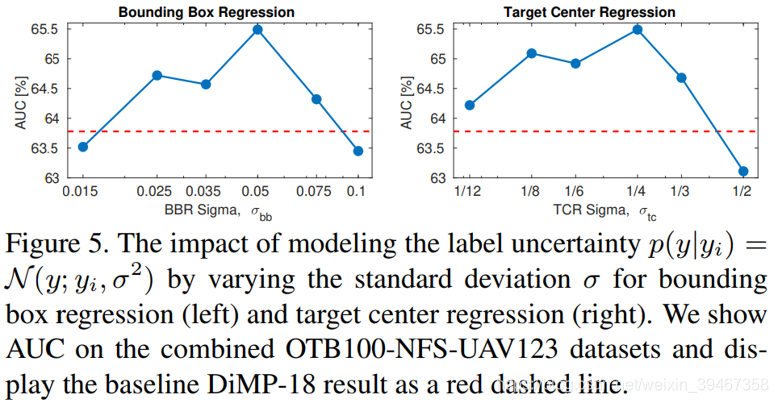
标签不确定性分析
结论:
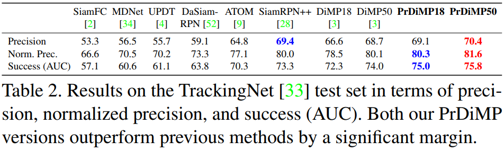
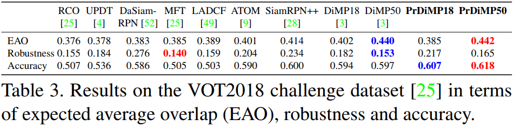
不同算法结果比较