论文全名:End-to-end representation learning for Correlation Filter based tracking
论文摘自CVPR 2017,由Jack Valmadre、Luca Bertinetto、Jõao F. Henriques、Andrea Vedaldi与Philip H. S. Torr撰写。该论文是Siamese-fc的改进版。
摘要
相关滤波器是一种训练线性模板以区分图像及其转换图像的算法。因为它在傅立叶域中快速运行,使得检测器在每帧都能重新训练,它非常适合物体跟踪。 但是,使用相关滤波器的先前工作是需要针对不同任务进行训练。
特点:是第一个将具有封闭式解决方案的相关滤波学习器作为深度神经网络中的一个分层来进行训练:这样可以学习与相关滤波器紧密耦合的深度特征。
实验表明,我们的方法具有重要的实际好处,在轻量级架构下实现高帧率运行。
1 前言
在线训练深度网络,从一个或几个例子中捕获未知的对象类,具有挑战性。跟踪目的是在序列开始时只监督边界框,从而在视频上对对象进行重检测。主要挑战是对目标对象先验知识的缺乏。
(1)带有随机梯度下降(SGD)的深度网络优化
特点:忽略先验知识的缺乏,将预训练的深度卷积神经网络(CNN)适应目标
缺点:有限的训练数据和大量参数成为问题;SGD对于在线调整来说计算相当昂贵。
(2)Siamese CNN
特点:不对网络进行在线调整;将深度嵌入用作通用的对象描述符;使用离线训练区分两个图像块是否包含相同的对象
缺点:使用固定标准来比较目标外观会阻止算法学习视频的特点。
(3)相关滤波器(CF)
特点:使用在线学习方法;其效率使得跟踪器能够在每一帧上实时调整模型;使用快速傅里叶变换(FFT)解决脊回归问题;比SGD更有效;与嵌入法相反,允许判别器针对特定视频。
(4)CNNs + CFs
特点:将CF的在线学习效率与CNN的离线学习功能相结合,改进了性能。
缺点:CF应用预先训练的CNN特征上,而没有两种方法的任何深度集成。(思考:CNN-CF组合是否也可以进行端到端训练?)
实现的关键步骤是将CF(训练学习问题的良药!)放入可分的CNN层,以便可以通过CF将错误送入CNN特征。因此,这需要区分大线性方程组的解。本文提供了相关滤波器导数的闭合表达式,具体方法:将CF纳入Siamese-fc框架,CF没有改善网络的效果,但实现了几千个参数的超轻量级网络,且速度很快。
2 相关工作
(1)自MOSSE之后,相关滤波器知名度直线提升,为简单起见,作者采用了相关滤波器的基本公式。
(2)在ECCVW2016时作者便提出了Siamese-fc孪生网络,所以在本论文中使用了该网络。
(3)相关滤波器层=计算正则化反卷积问题
(4)对于训练期间反向传播梯度优化算法,作者研究了SVD和Cholesky分解的反向传播形式(梯度下降能够计算线性方程组与特征值),通过求解线性方程组,实现一种有效的反向传播过程,其中矩阵为循环矩阵。
(5)使用传统学习问题传播梯度。
3.具体思想
我们随后推导出我们网络中主要新成分的评估和反向传播的表达式,
相关滤波器层在前向传递中在线学习(第3.4节)
3.1 Siamese-fc网络(网络框架)
与全卷积的Siamese框架不同,该网络输入包括训练图x'和测试图z'的对(x',z')。x'表示以初始帧中的目标对象为中心的图像块,z'表示下一帧中较大的搜索区域。它们都由可学习参数ρ的CNN fρ处理。生成两个特征映射,进行交叉互关联,使目标位置对应最大响应值,与全卷积的Siamese框架类似,离线训练网络,从视频集合中获取数百万随机对(x'i,z'i)。对应一个值为{-1,1}的ci的空间映射(真实对象位置属于正样本,其余属于负样本)。损失函数定义为
。
3.2 跟踪算法(跟踪框架)
采用简单的跟踪算法来评估相似度函数,在线跟踪时,搜索图像块大小为之前帧中目标对象大小的四倍,将目标对象与搜索区域的特征表示进行比较,用前向模式评估网络,对象的新位置为得分最高的位置。
区别:原始的Siamese-fc网络简单地将每个帧与对象的初始帧进行比较,而该框架在每个帧中计算一个新template,然后将其与前一个template相结合。
3.3 CFNet(相关滤波网络)
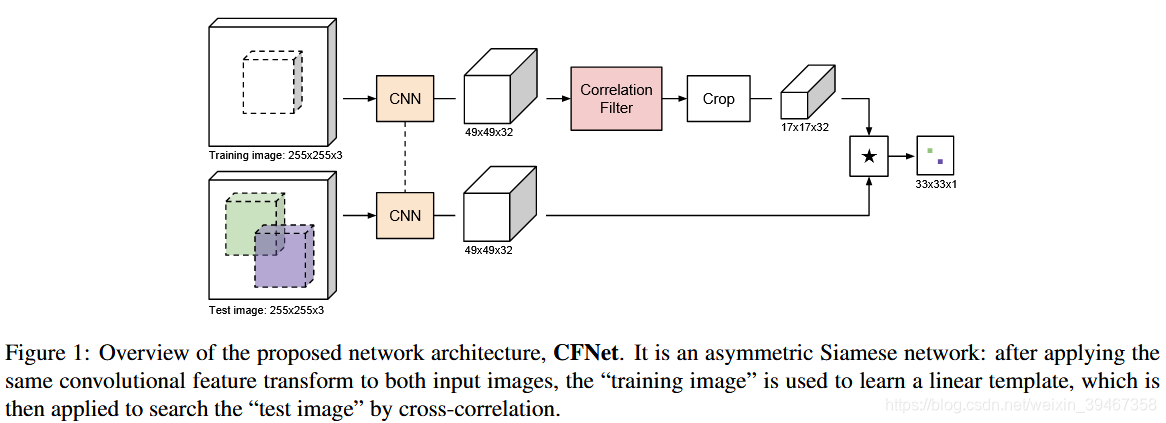
对两个输入图像进行相同的卷积特征变换后,“训练图x”用于学习线性template,然后通过 互相关搜索“测试图z”。
一、作者使用x和互相关符之间的相关滤波块代替式(1)的网络,最终的架构如图1所示,公式为
(1)与KCF核心相同,通过求解傅立叶域中的脊回归问题,对于训练特征图x,从w =ω(x)中计算出标准的CFtemplate w(更具鲁棒性);
(2)为了让结果适合于逻辑回归,引入标量参数权重s和偏差b;
(3)将式(2)中的g替换成h,训练方法与Siamese-fc相同。
二、在2015年提出的SRDCF与CFLB中,都提到了扩大相关滤波器中的图像区域后效果明显提升;为了减少循环边缘的影响,特征图x预先乘以余弦窗(MOSSE)并裁剪最终的template(一作的又一理论性论文)。
三、提出将CF template放入网络,达到端到端训练。
3.4 相关滤波器(在傅里叶域中用CF以封闭式反向传播梯度)
一、公式
与KCF算法类似,给定图像x∈Rm×m,CF template 

,其中
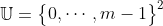



,其中n=|
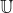
(一)先前条件:
将损失问题等价成约束优化问题
,即,用拉格朗日求鞍点法求解该方程(对应参数
求偏导)
,得到:
,
。其中
,令
,那么
(25),当特征数d大于核矩阵维度n时,对偶解比原解效果更好。
(二)对于单通道CF:
(1)由于矩阵X(由向量x循环组成)为对称矩阵,有定义(循环互相关计算中第u个元素):
,那么由式(25)得:
(28)。
(2)对于任意的向量z,利用式(28)和傅立叶变换与逆变换,有:
,与
结合, 有:
,则有:
。
(3)同样的,对于上面提到的
与
,可以解出
。
得到方程:
与对应傅里叶域中:
。
附:至于式(32)中进行傅立叶变换后x变成了它的共轭,可以从KCF的4.4节中找出答案:
。
(三)对于多通道CF:
在KCF中提到,对偶空间在多通道情况下效率更高(相比单通道),且计算与通道数量成线性关系。对于具有k个通道的信号,对应的式(21)
与式(22)
,可以得出
(1)
;
(2)核矩阵
;
(3)
得到方程:
与对应傅里叶域中:
。
二、滤波器的反向传播
在计算图上,采用变量与变量
(根据线性函数y=f(x)计算),最终损失为
,偏导数为
,反向传播图是从∇y到∇x的线性图。
(一)矩阵微积分:
反向传播是通过计算输出
来间接计算输入
。
在程云鹏等著作的《矩阵论》中p169(网页对应的第95页)例3.15给出了该式的详细证明:
即有:
。
(二)定义反向传播:
定义反向传播的线性映射:
,那么对于
都为实数域中的向量,有
(41)与两个输入的梯度相关:
。
反向传播图是线性图,作者采用Parseval定理,它表明傅里叶变换是单一的(除比例因子):。
对式(31)求微分得到: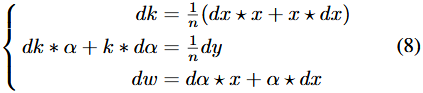
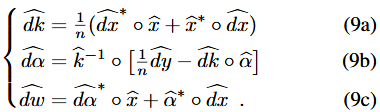
(三)单通道CF中的反向传播:
上面提到,反向传播图是作为差分线性图的伴随。 我们可以自由地在傅里叶域中获得这些伴随映射,因为Parseval定理提供了内积的存储。
(1)设
为
的特征映射,记
,
,对式(41)做傅里叶变换(这里设
),
。可得:
。那么根据输入的梯度相关性,可得:
。
(2)类似的,对于为
的特征映射,记
,
,
那么对应地,
,根据输入的梯度相关性,分别得:
。
(3)类似的,对于
为
的特征映射,记
,
,
那么对应地,
,根据输入的梯度相关性,分别得:
。
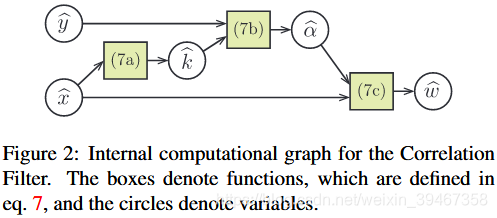
综上所述,根据图2的的整体反向传播图,最终结果为: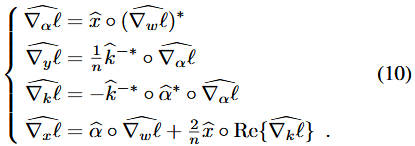
(四)多通道CF中的反向传播:
与一公式中的(三)类似,对式(37)用微分方法进行反向传播运算,得到傅里叶域中的:
。与上面的单通道反向传播计算类似,我们也可以得到类似式(10)的方程:
,且计算与通道数量成线性关系。
另外,我们注意到响应y具有损失的梯度,可以优化该参数。然而在MOSSE与KCF中,并未发现学习这个参数可以提高精度。
4. 实验
主要目的:研究训练期间加入CF的效果。
实验对比:
(1)与本论文第一版本Siamese-fc相比较;(2)将端到端训练的CFNet与它的变形(针对不同任务进行不同训练)进行比较。
4.1 评估标准
训练集:ImageNet2015的3862个训练视频。(最多相隔100帧)两帧图像中随机采样12对随机提取,进行100次迭代。在跟踪期间,以几何步长1.04来实现在尺度空间中的跟踪。将缩放对象的响应乘以0.97来更新比例。为了避免对象大小的突然转换,使用具有学习率0.6的滚动平均值来更新比例。
验证集:VOT-2014,VOT-2016和Temple-Color数据集,一共129个视频;
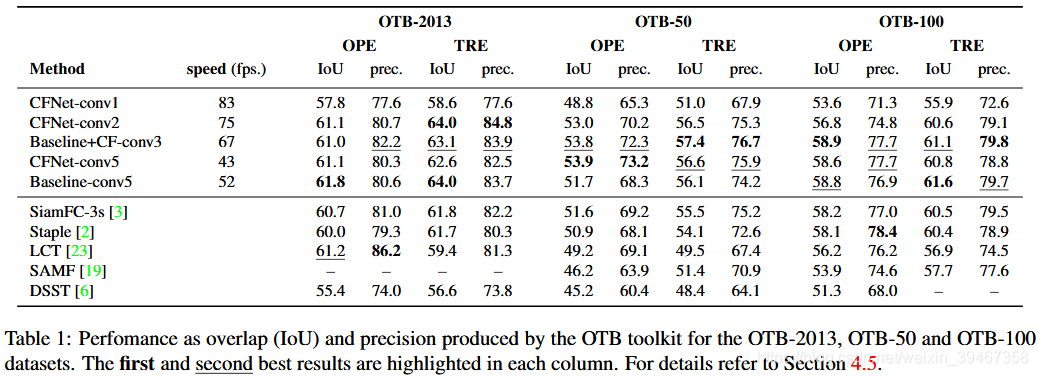
测试集:OTB-2013,OTB-50和OTB-100数据集。
特点:实验中,使用相同的“自然”超参数集,没有针对任何特定方法进行调整;使用区间为55,66,...,100这十个帧数间隔训练网络。
评估标准:(1)与OTB2013与OTB2015一样:计算平均IOU;(2)TRE:选择三个等间隔点,从每个点运行跟踪器,当IOU=0时,终止跟踪其运行(后余帧默认IOU=0)。
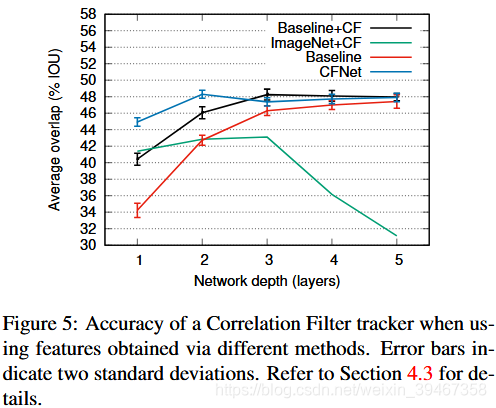
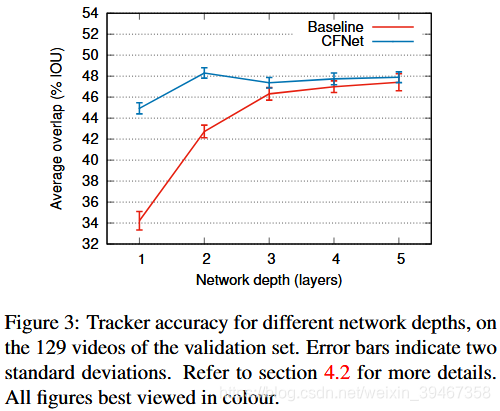
4.2 与Siamese-fc比较
算法:Siamese-fc与CFNet
注意:上图比较了两种方法对不同深度网络验证集的准确性。深度为n的特征提取网络在第n个线性层(包括ReLU,不包括池化层)后终止。
与原Siamese-fc不同点:(1)将网络的总步幅从8减少到4(conv1为2,pool1为2)【减少小特征】;(2)将输出层通道从128固定为32【速度更快】。
总结:(1)浅层网络用于计算特征时,CFNet明显优于Siamese-fc;(2)CFNet相对不受网络层数的影响;(3)当有足够的模型容量和可用数据时,CFNet变得多余;(4)更新模板对两个算法效果都有明显提升。
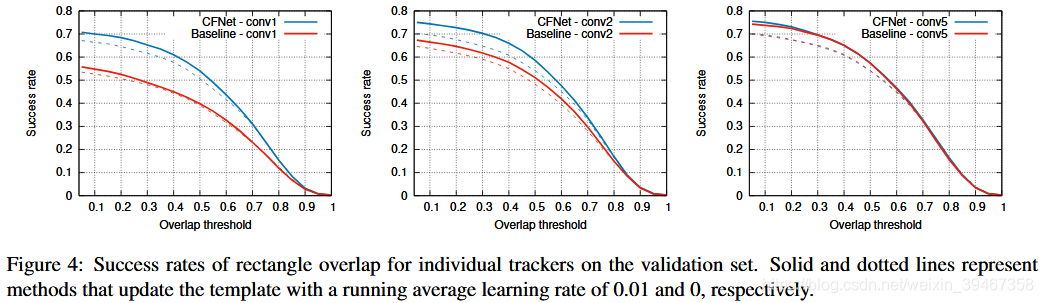
4.3 其他实验
Baseline + CF:训练Siamese-fc+跟踪期间CF。当添加更多卷积层时,性能并未有所提升。
CFNet-const:对于多通道CF:,解决了在测试时脊回归问题,(网参)拉格朗日乘子α:离线训练,测试不变。
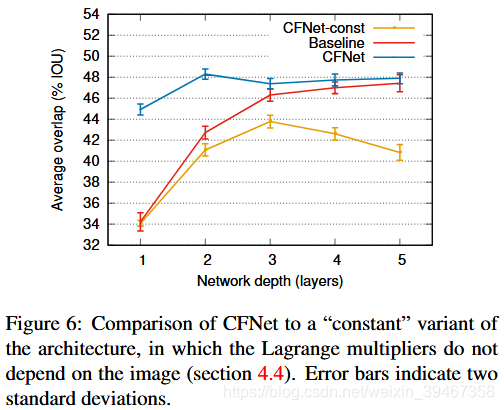
说明 反向传播的重要性
训练:(1)数据结果为OTB2013;(2)在每个算法中加入不同的(300次迭代)超参;(3)对于OTB2013中的灰度图像,使用所有灰度序列重新训练每个算法。
评估:(1)OPE:算法在图像序列只运行一次;(2)TRE:每个算法从20个不同的起点开始,一直运行最后。
总结:当网络较浅时,CFNet效果很好,需要较少的操作和较少的存储

GPU:NVIDIATitan X
CFNet-conv2:(1)速度75FPS;(2)比Baseline-conv5(基于Siamese-conv5)参数少4%;(3)存储空间600kB
5. 结论
(1)提出CFNet(非对称架构):运用了反向传播梯度,使用在线训练优化基础特征表示。为循环方程系统建立了有效的反向传播图。
(2)CFNet网络对深度层数不太敏感。
(3)对未来研究:自适应扩展,以及通过学习来将反向传播梯度用于一次性学习和领域适应等相关任务。