前段时间整理了一个预测的基本思考框架和常见的方法，其中提到了ARIMA模型，在《大数据预测》那本书里，ARIMA是单独开辟一章讲的，比较复杂和难理解的一个模型，自己最近找了点资料粗浅学习了一下理论，并尝试用Python实现一下。

一、时间序列数据及其预处理

1.时序数据

时序数据顾名思义就是随着时间而变动的数据，是指某个个体在不同时间点上收集到的数据。已经被收集(或者叫观察)到的数据其实是时间序列变量的一个观察值，但由于时间的不可逆性，每一个时间点的变量有且仅能有一个观察值，我们用这些观察值拟合预测模型，用来预测未来时刻时间序列变量的值(此时，未发生的时间序列变量是一个随机变量)。

2.时序数据预处理

时序数据的预处理主要是 平稳性和随机性检验，根据检验结果的不同，用不同的模型对数据进行建模。 纯随机序列，又称为白噪声序列，序列的变量之间无任何关系，因此没有分析价值；平稳非白噪声序列，其均值和方差是常数，目前有比较成熟的模型对其进行模拟，主要是 AR(Autoregressive model)自回归模型，MA(Movingaverage model)移动平均模型、以及ARMA-一个AR和MA结合的模型。

(1)平稳性检验

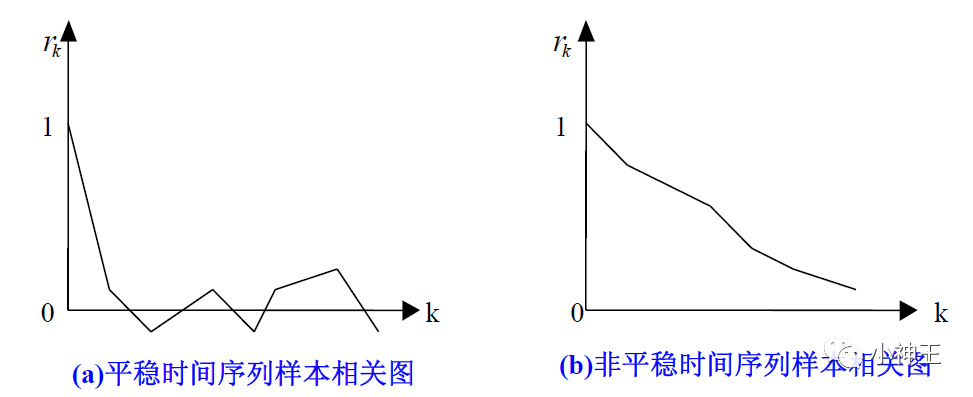
平稳性检验的基本原理是检验不同时间点时序变量之间的相关关系，由于是一个时间序列数据的不同时刻之间的相互比较，因此取名为自协方差函数和自相关系数，但基本原理和协方差函数、相关系数类似，当一个时间序列有为常数的均值和方差，且其自协方差函数只跟时间间隔有关，即γ(t,s) =γ(k,k+s-t) ，其中γ是自协方差函数。 平稳性检验的方法分为两类，一类是偏主观和模糊的图示检验，一类是比较精确的数学检验。 第一类主要是用时序图和自相关图进行观察，如果一个时间序列的时序图围绕某一个常数上下波动，且波动范围有界，可以认为是平稳的，除此之外，如果自相关图中自相关系数比较快速衰减到0，并且在零附近震荡，可以认为序列是平稳序列，这是因为平稳序列通常具有短期相关性，随着延迟期数的增加，变量之间的相关关系会指数降低。

第二类数据的检验方法是 单位根检验。单位根又称为单位圆，指模型的特征方程的根和1的关系，如果模型的特征根小于1，则序列非平稳，如果特征根大于1，则序列平稳。

(2)白噪声检验

白噪声序列的各个序列值之间没有任何关系，即γ(k)=0，在实际中，只要序列变量之间的协方差系数在0值附近波动，就可以认为是白噪声序列了。

二、常用模型

平稳时间序列的建模通常是AR、MA和ARMA模型，它们都是一种多元线性回归模型。

1.AR模型

这个模型的定义是t时刻的序列取值和前p期的序列值有关，且是前p期的线性组合。这个比较容