
1 简单的Octave / MATLAB功能
ex1.m的第一部分为Octave/MATLAB作业提交练习。 在文件warmUpExercise.m中,找到Octave / MATLAB函数的提纲处。 填写下面的代码,修改为返回5 x 5的单位矩阵:
A 完成后,运行ex1.m(假设命令窗口位于正确的目录中,在Octave / MATLAB命令窗口输入“ ex1”),将看到类似于以下内容的输出:
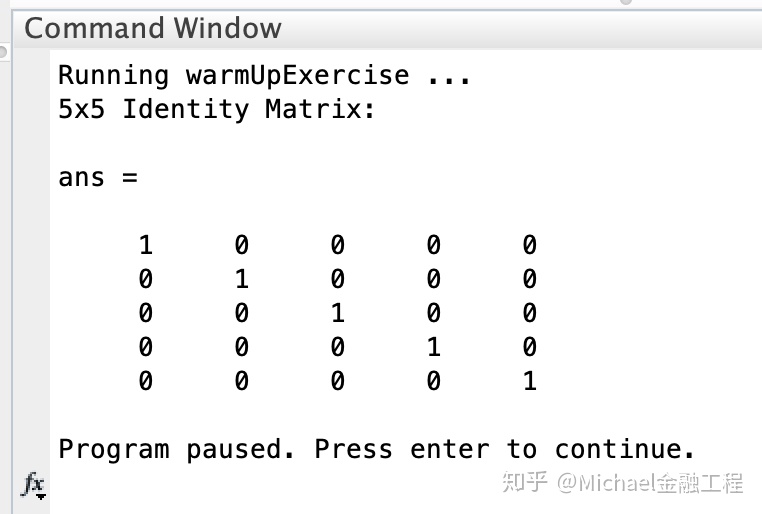
1.1 提交答案
完成练习的一部分后,在Octave / MATLAB命令行中通过输入 Submit() 来提交作业答案。 提交脚本将提示您输入登录电子邮件和提交令牌(在COURSERA网站查看),并询问是否提交的文件。
现在,提交解决方案。
可以多次提交解决方案,只会考虑最高分。
2 单变量线性回归
在本练习的这一部分中,将使用一个变量实现线性回归,以预测食品卡车的利润。 假设您是一家餐饮连锁店的CEO,并且正在考虑将不同的城市开设新的门店。 该连锁店已经在各个城市开了卡车,您可以获得城市的利润和人口数据。您想使用此数据来帮助您选择要扩展到下一个城市。
文件 ex1data1.txt 包含线性回归问题的数据集。 第一列是城市的人口,第二列是该城市的食物卡车的利润。 利润的负值表示损失。已经设置了ex1.m脚本来为您加载此数据。
2.1 绘制数据
在开始任何任务之前,通过可视化了解数据通常很有用,对于此数据集,您可以使用散点图来可视化数据,因为它仅具有两个要绘制的属性(利润和总体)。(您在现实生活中会遇到的许多其他问题是多维的,无法在二维绘图中绘制。)
在 ex1.m 中,数据集从数据文件加载到变量X和y中:
data 接下来,脚本调用 plotData 函数创建数据的散点图。 您的工作是完成plotData.m绘制图; 在以下代码中修改文件并填充文件:
plot现在,当您继续运行ex1.m时,我们的最终结果应下图所示,带有相同的红色“ x”标记和轴标签。
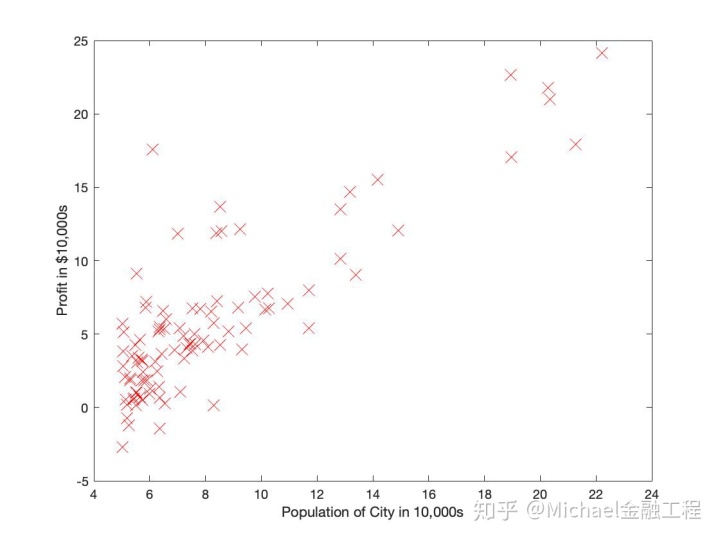
要了解有关plot命令的更多信息,可以在Octave / MATLAB命令提示符下键入help plot或在线搜索绘图文件。 (要将标记更改为红色的“ x”,我们将选项“ rx”与plot命令一起使用,即plot(..,[此处为您的选项],..,“ rx”);)
2.2 梯度下降
在这一部分中,您将使用梯度下降法将线性回归参数θ拟合到我们的数据集中。
2.2.1 更新公式
线性回归的目的是最小化成本函数:
回想一下,模型的参数是
随着梯度下降的每一步,您的参数
实施注意:我们将每个示例作为一行存储在Octave / MATLAB的X矩阵中。 为了考虑截距项(
2.2.2 实施
在ex1.m中,我们已经设置了用于线性回归的数据。 在接下来的几行中,我们向数据添加另一个维,以适应θ0截距项。 我们还将初始参数初始化为0,将学习率alpha初始化为0.01。
X 2.2.3 计算成本函数
当执行梯度下降以最小化成本函数时,通过计算成本来监控收敛是有帮助的。 在本节中,将实现一个计算
任务是完成文件 computeCost.m 中的代码,该文件是一个计算
完成后,下一步 ex1.m 将使用初始化为零的 θ 运行一次computeCost,然后您应该会看到代价函数值为32.07。
现在,您应该提交解决方案。
function2.2.4 梯度下降
接下来将在文件 gradientDescent.m 中实现梯度下降。已经编写了循环结构,只需要在每次迭代中为θ提供更新。
在编程时,请确保了解要优化的内容和更新的内容。记住成本
验证梯度下降是否正常工作的一种好方法是查看
完成后,ex1.m将使用最终参数来绘制线性拟合。结果应类似于下图:
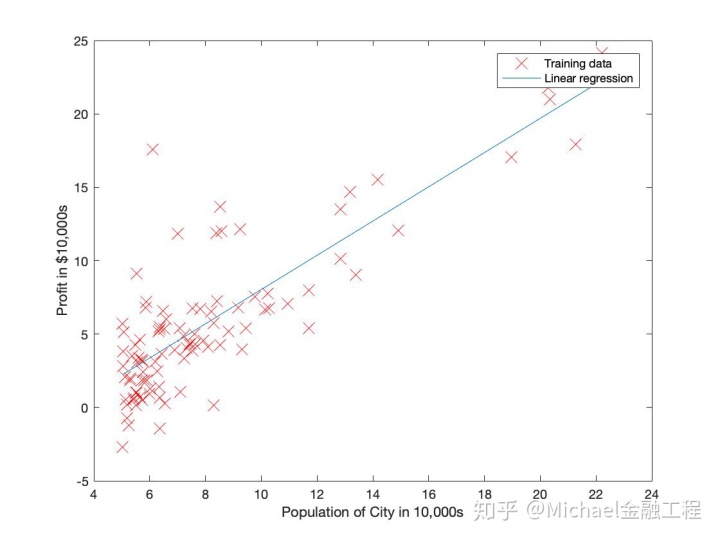
最终的θ值也将用于预测35,000和70,000人区域的利润。请注意,ex1.m中的以下几行使用矩阵乘法而不是显式求和或循环来计算预测。这是Octave / MATLAB中代码向量化的示例。
现在,提交答案
predict1 2.4 可视化
为了更好地理解成本函数
在 ex1.m 的下一步中,设置了代码,以使用您编写的computeCost函数在值的网格上计算
执行完这些行后,将拥有
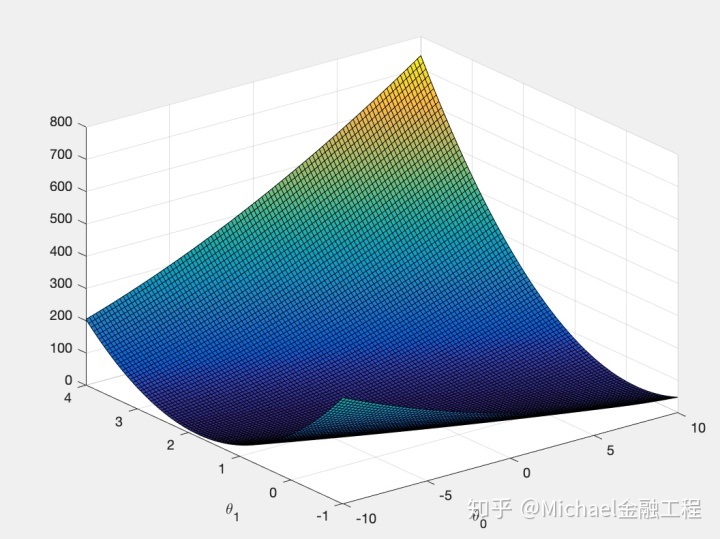
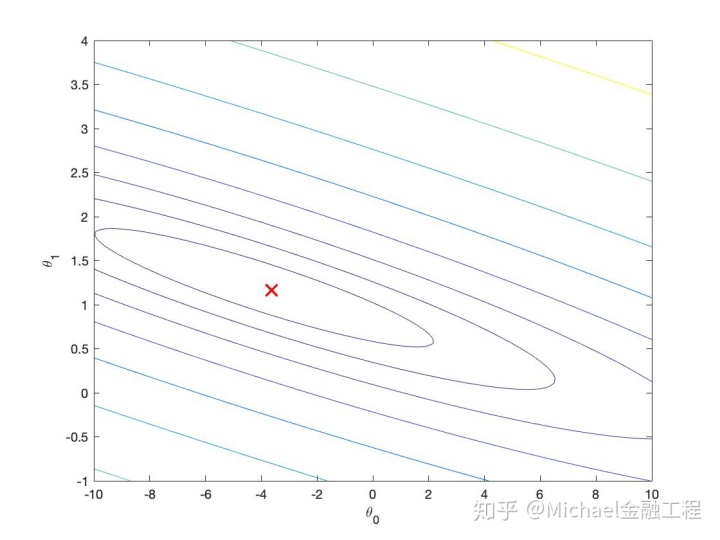
这些图的目的是展示
如有问题,欢迎私信交流。