cv曲线面积的意义_关于离散信号Parseval定理的物理意义

奥本海姆所著《信号与系统》（刘树棠译版）中关于Parseval定理的描述如下：

信号的能量既可以按每单位时间的能量在整个时间内积分出来，也可以按每单位频率的能量在整个频率范围内积分而得到。

简单地讲，信号从时域变换为频域后，总能量保持不变。时域连续信号的Parseval定理表达式如下：

本文仅针对离散傅里叶变换（DFT）后的信号Parseval公式做一些探讨，DFT的内涵就是将时域上长度为N的序列转化为频域上长度为N的复序列，正变换和逆变换通常有以下两种形式：

或

其中

为时域序列，

为频域序列，两种变换方法的区别在于系数

所放的位置不同，算法上并无本质差别，FFT作为快速实现DFT的算法之一，MATLAB中采用的是第一种方法。基于此，

离散信号Parseval定理表达式如下：

等式左边很容易让人联想到信号的总能量，但又似是而非，首先连续信号的能量

为信号的平方对时间的积分，假设

，可以理解为曲线

与横坐标轴所围的面积。用离散信号来对连续信号的能量进行近似的过程如下图：

图1 用离散信号来近似连续信号的积分

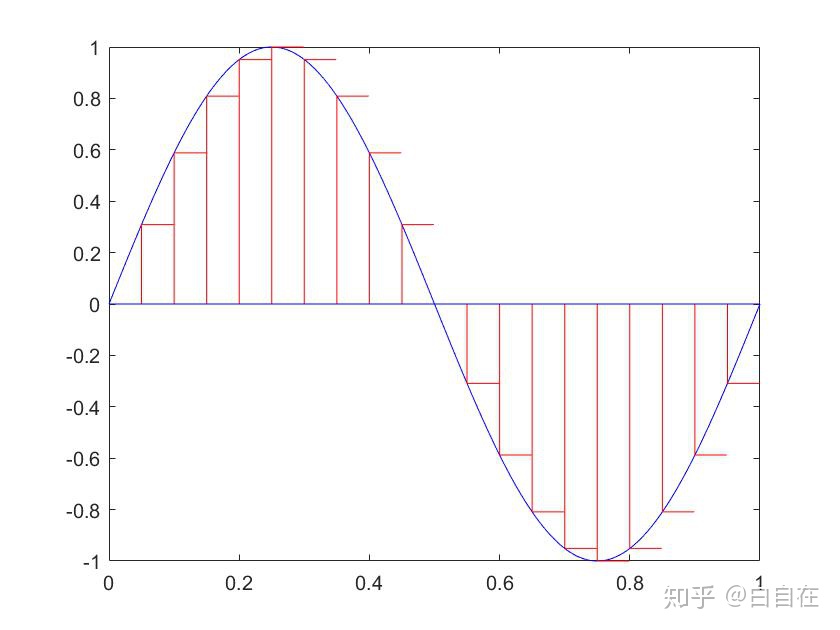
所以离散信号总能量的计算应该为：

其中

为采样间隔，

越小，图中红色矩形的面积之和越接近于蓝色曲线与坐标轴围成的面积。那么离散信号Parseval定理表达式左右同时乘以

得到：

现在等式左边变为信号的总能量，具有了实际物理意义，那等式右边作何理解，咋一看什么都不是。由于等式成立，可以猜想等式右边应该也是能量的一种表达形式，但是如何将其与信号能量联系起来呢？

首先FFT计算结果的每一点代表了该频点下信号的幅值特性，其幅度大小为该频点时域信号幅值的

倍（前提条件是N等于2的整数次幂，即MATLAB在运算时未对序列补零），对于单频信号

一个周期内的能量为：

即单频信号周期内的能量等于幅值*周期/2，也就是说单频信号的能量仅用幅值和时间两个量就能表征。

现在回到Parseval定理等式的右边，由于FFT结果关于0对称，有：

而

恰好等于对应频点单频信号的幅值，于是等式右边用信号幅值和时间两个量，表达了

所有单频信号在时间T内的能量之和。

通过上述分析离散信号Parseval定理的物理意义，可以更好地帮助理解该等式的内涵。